Матрица Кирхгофа

Определение:

Матрицей Кирхгофа простого графа [math]G = (V,E) [/math] называется матрица [math] K (|V| \times |V|) = \parallel k_{i,j} \parallel [/math], элементы которой определяются равенством: [math] k_{i,j} = \begin{cases} \deg(v_i), \ i = j \\ -1, \ (v_i,v_j) \in E \\ 0, \mbox{ otherwise}. \end{cases} [/math]

Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении [math]i[/math]-й строки и [math]j[/math]-го столбца ([math]i \ne j[/math]) стоит [math]-1[/math], если вершины с номерами [math]i[/math] и [math]j[/math] смежны, и [math]0[/math] в противном случае.

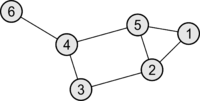
Пример матрицы Кирхгофа

Граф	Матрица Кирхгофа
	[math]\left(\begin{array}{rrrrrr} 2 & -1 & 0 & 0 & -1 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & -1 & 0 & 0\\ 0 & 0 & -1 & 3 & -1 & -1\\ -1 & -1 & 0 & -1 & 3 & 0\\ 0 & 0 & 0 & -1 & 0 & 1\\ \end{array}\right)[/math]

Некоторые свойства

Утверждение:

Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю: [math]\ \sum_{i=1}^{|V|} k_{i,j} = 0[/math].

Утверждение:

Определитель матрицы Кирхгофа равен нулю: [math]\det K=0[/math]

[math]\triangleright[/math]

[math] \det K = \begin{vmatrix} k_{1, 1} & k_{1, 2} & \cdots & k_{1, |V|} \\ k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} \end{vmatrix} [/math] Прибавим к первой строке все остальные строки (это не изменит значение определителя): [math]\begin{vmatrix} k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} \\ k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} \end{vmatrix} [/math] Так как сумма элементов каждого столбца равна [math]0[/math], получим: [math]\det K = \begin{vmatrix} 0 & 0 & \cdots & 0 \\ k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} \end{vmatrix} = 0 [/math]

[math]\triangleleft[/math]

Утверждение:

Матрица Кирхгофа простого графа симметрична: [math]\ k_{i,j} = k_{j,i}\quad i,j=1, \ldots, |V|[/math].

Утверждение:

Связь с матрицей смежности: [math] K = \begin{pmatrix} \mathrm{deg}(v_1) & 0 & \cdots & 0 \\ 0 & \mathrm{deg}(v_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathrm{deg}(v_n) \end{pmatrix} - A, [/math] где [math]A[/math] — матрица смежности графа [math]G[/math].

Утверждение:

Связь с матрицей инцидентности: [math] K = I \cdot I^T, [/math] где [math]I[/math] — матрица инцидентности некоторой ориентации графа.

Утверждение:

[math]0[/math] является собственным значением матрицы, кратность его равна числу компонент связности графа.

[math]\triangleright[/math]

Собственным значением матрицы называют значения [math]\lambda[/math], которые удовлетворяют уравнению: [math]\begin{vmatrix} k_{1, 1} - \lambda &k_{1, 2} & \cdots & k_{1, |V|} \\ k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V| - \lambda} \end{vmatrix} = 0 [/math] Прибавим к первой строке все остальные строки (это не изменит значение определителя): [math]\begin{vmatrix} k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} - \lambda & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} - \lambda & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} - \lambda \\ k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda \end{vmatrix} [/math] Так как сумма элементов каждого столбца равна [math]0[/math], получим: [math]\begin{vmatrix} - \lambda &-\lambda & \cdots & - \lambda \\ k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda \end{vmatrix} = 0 [/math] [math]- \lambda \begin{vmatrix} 1 & 1 & \cdots & 1 \\ k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ \vdots & \vdots & \ddots & \vdots \\ k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda \end{vmatrix}= 0. [/math] Следовательно, [math]0[/math] является собственным значением. Доказательство кратности: Пусть дан граф [math]G[/math] c [math]n[/math] компонентами связности. Перенумеруем его вершины так, чтобы сначала шли вершины первой компоненты связности, затем второй и т.д. Тогда матрица Кирхгофа примет блочно-диагональный вид, и [math]i[/math]-тый блок этой матрицы будет являтся матрицей Кирхгофа для [math]i[/math]-той компоненты связности. Из свойства блочно-диагональной матрицы [math]\det K = \det K_{1} \cdot \det K_{2} \cdot \ldots \cdot \det K_{n}[/math], где [math]K_{i}[/math] — матрица Кирхгофа для [math]i[/math]-той компоненты связности, и свойства, доказанного выше, [math]\det K_{i} = - \lambda \cdot det X_{i} \quad \Rightarrow \quad \det K = (-1)^{n} \cdot \lambda^{n} \cdot \det X_{1} \cdot \det X_{2} \cdot \ldots \cdot \det X_{n}[/math]

[math]\triangleleft[/math]

См. также

• Связь матрицы Кирхгофа и матрицы инцидентности
• Подсчет числа остовных деревьев с помощью матрицы Кирхгофа

Источники информации

• Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы. стр. 18
• Википедия — Матрица Кирхгофа