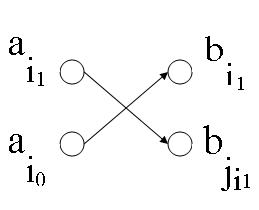Материал из Викиконспекты
Граф замен (англ exchange graph) — специальный ориентированный двудольный граф, фигурирующий в теореме Эдмондса-Лоулера.
Пусть даны матроиды [math]M_1 = \langle S, \mathcal{I}_1 \rangle[/math], [math]M_2 = \langle S, \mathcal{I}_2 \rangle[/math], множество [math](\mathcal{I}_1 \cap \mathcal{I}_2)[/math]. Введем граф замен.
| Определение: |
| Граф замен для двух матроидов [math]D_{M_1, M_2}(I)[/math] — граф, левой долей которого являются элементы множества [math]I[/math], правой — все остальные элементы [math]S[/math] и в котором проведены ребра [math](y, z): y \in I, z \in S \setminus I, I \setminus y \cup z \in \mathcal{I}_1[/math], а также [math](z', y'): y' \in I, z' \in S \setminus I, I \setminus y' \cup z' \in \mathcal{I}_2[/math] |
Пусть [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}, P[/math] — кратчайший путь в [math]D_{M_1, M_2}(I)[/math] из [math]X_1[/math] в [math]X_2[/math]. Тогда алгоритм с помощью этого пути либо определяет максимальность набора [math]I[/math], либо позволяет найти набор большей мощности.
Граф замен
[math]D_{M_1, M_2}(I)[/math]Также существует граф замен для одного матроида.
| Определение: |
| Пусть дан матроид [math]M = (S, \mathcal{I})[/math] и независимый сет [math]I \in \mathcal{I}[/math]. Тогда граф замен [math]D_{M}(I)[/math] (или просто [math]D(I)[/math]) — это двудольный граф с долями [math]I[/math] и [math]S \setminus I[/math] с рёбрами между [math]y \in I[/math] и [math]x \in S \setminus I[/math] если [math] I - y + x \in \mathcal{I} [/math] |
| Лемма (о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем): |
Пусть дан двудольный граф замен. В его правой доле выделено два подмножества вершин [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}[/math]. [math]P[/math] — кратчайший путь из [math]X_1[/math] в [math]X_2[/math].
[math]G'[/math] — подграф [math]G[/math], включающий множество вершин, лежащих на пути [math]P[/math]. Тогда в [math]G'[/math] существует единственное полное паросочетание. |
| Доказательство: |
| [math]\triangleright[/math] |
- Так как в правой доле полученного графа [math]G'[/math] вершин на одну больше, чем в левой, добавим в [math]G'[/math] фиктивную вершину и отнесем ее к левой доле.
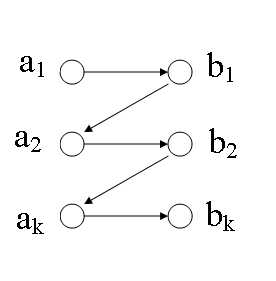
- Рассмотрим [math]P = (a_1, b_1, a_2, b_2, \ldots , a_k, b_k)[/math] — кратчайший путь из условия, где [math]a_1[/math] — фиктивная вершина (рис. 1).
- В таком случае, полное паросочетание — это набор ребер [math]\langle a_i,b_i \rangle[/math].
Докажем единственность.
- Пусть существует другое паросочетание [math]\langle a_i, b_{j_i} \rangle[/math]. Тогда пусть [math]i_0 = \min \{ i \: \mid \: j_i \lt i \}[/math].
- Обозначим [math]j_{i_0}[/math] как [math]i_1[/math]. Заметим, что [math]i_1 \lt i_0[/math] (так как [math]j_{i_0} \lt i_0 [/math] по определению [math]i_0[/math]) и поэтому не может быть [math]j_{i_1} \lt j_{i_0}[/math], ведь [math]i_0[/math] — минимальное из соответствующего множества. Так же невозможно [math]j_{i_1} = j_{i_0}[/math], поскольку тогда [math]a_{i_0}[/math] и [math]a_{i_1}[/math] имели бы одинаковую пару.
- Следовательно, [math]j_{i_1} \gt j_{i_0}[/math] (рис. 2). Это значит, что существует путь [math]P_1 = (a_1, b_1, \ldots, a_{i_1}, b_{j_{i_1}}, a_{j_{i_1} + 1}, \ldots, a_k, b_k )[/math] короче, чем [math]P[/math], что противоречит тому, что [math]P[/math] — кратчайший путь.
|
| [math]\triangleleft[/math] |
| Лемма (о паросочетании в графе замен): |
Пусть [math]M = \langle X,\mathcal{I} \rangle [/math] — матроид. Множества [math]A, B \in \mathcal{I}[/math] — независимы, причем [math]|A| = |B|[/math]. Тогда двудольный граф [math]D_{M}(A)[/math] содержит полное паросочетание на [math]A \bigtriangleup B[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Индукция по [math]|A \bigtriangleup B|[/math].
- При [math]|A \bigtriangleup B| = 0 [/math] имеем пустое паросочетание.
- Пусть верно для [math]|A \bigtriangleup B| = N[/math].
- Пусть [math]k = |A| = |B|[/math] и [math]|A \bigtriangleup B| \geqslant 1[/math].
- Рассмотрим матроид [math]M_1 = \langle X, \{ A \mid A \in \mathcal{I}, |A| \leqslant k \} \rangle[/math]. Множества [math]A, B \in \mathcal{I}[/math], [math]|A| = |B|[/math] и матроид [math]M_1[/math] не содержит множеств больших, чем [math]A[/math], а значит они являются базами для матроида [math]M_1[/math].
- По сильной теореме о базах: [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y \in \mathcal{I}[/math] и [math](B \setminus y) \cup x \in \mathcal{I}[/math]
- Из этого следует, что множества [math]A' = (A \setminus x) \cup y [/math] и [math]B' = (B \cup x) \setminus y[/math] являются независимыми, а также базами [math]M_1[/math]. Заметим, что [math]|A' \bigtriangleup B'| \lt |A \bigtriangleup B|[/math], [math]|A' \bigtriangleup B'| = N[/math], [math]|A \bigtriangleup B| = N+1 [/math]. По предположению индукции у [math] |A' \bigtriangleup B'|[/math] есть полное паросочетание.
- По теореме о базах [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y
\in \mathcal{I}[/math], следовательно по определению графа [math]D_M(A), (x, y) \in D_M(A)[/math]. Тогда [math]N \cup {(x, y)}[/math] составляет полное паросочетание на [math]|A \bigtriangleup B|[/math]. Индукционный переход доказан.
|
| [math]\triangleleft[/math] |
| Утверждение: |
Пусть двудольный граф [math]G[/math] содержит единственное полное паросочетание [math]M[/math]. Тогда можно упорядочить вершины левой [math](a_i \in A)[/math] и правой [math](b_i \in B)[/math] долей таким образом, что [math]\forall j \gt i : (a_i b_j) \notin G[/math]. При этом рёбра паросочетания будут иметь вид [math](a_i b_i)[/math]. |
| [math]\triangleright[/math] |
|
Индукция по [math]|A|[/math].
- При [math]|A|=1[/math] утверждение очевидно.
- Пусть верно для [math]|A|=n-1[/math].
- Рассмотрим [math]|A|=n\gt 1[/math]. Возьмем произвольную вершину в левой доле. Будем строить из неё чередующуюся цепь, добавляя по очереди ребро, входящее в [math]M[/math], и ребро, не входящее в [math]M[/math]. Заметим, что такой путь не содержит циклов (циклы нечётной длины невозможны, так как граф двудольный, циклы чётной длины отсутствуют из-за единственности паросочетания). Если последнее добавленное ребро не принадлежит [math]M[/math], то присоединим к цепи ребро из [math]M[/math], инцидентное последней вершине. Значит, построение цепи прервется только при добавлении ребра из [math]M[/math] при достижении вершины степени [math]1[/math].
- Таким образом, последнее ребро в цепи имеет вид [math]\langle a, b \rangle \in M[/math], где [math]a \in A, b \in B, \deg b = 1[/math]. Положим [math]a_n=a, b_n=b[/math]. Для [math]G \setminus \{a_n \cup b_n \}[/math] утверждение верно по предположению индукции. С другой стороны, так как [math]\deg b_n = 1[/math], то [math] \langle a_i, b_n \rangle \notin G[/math] при [math]i\lt n[/math], поэтому для [math]j = n[/math] утверждение также верно.
|
| [math]\triangleleft[/math] |
| Лемма (о единственном паросочетании в графе замен): |
Дан матроид [math]M = \langle X,I \rangle [/math]. Пусть двудольный граф [math]G_M(A) = \{ (x, y) \mid x \in A, y \notin A, A \setminus x \cup y \in I \}[/math] содержит единственное полное паросочетание на [math]A \bigtriangleup B[/math], где [math]A\in I[/math] и [math]|A| = |B|[/math]. Тогда [math]B \in I[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
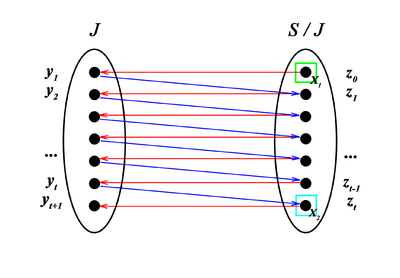
Упорядочим вершины левой [math](y_i \in A \setminus B)[/math] и правой [math](z_j \in B \setminus A)[/math] долей таким образом, что [math]\forall j \gt i : \langle y_i, z_j \rangle \notin G_M(A)[/math]. При таком упорядочивании ребра паросочетания имеют вид [math] \langle y_i, z_i \rangle[/math].
- Требуется доказать, что [math]B[/math] независимо.
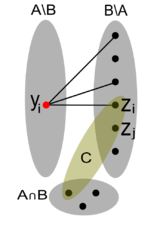
- Предположим обратное. Пусть [math]B \notin I[/math]. Tогда существует цикл [math]C \subset B[/math].
Выберем минимальное [math]i[/math] такое, что [math]z_i \in C[/math]. Так как [math]\forall j \gt i : \langle y_i, z_j \rangle \notin G_M(A)[/math], то [math]A \setminus y_i \cup z_j \notin I[/math]. Cледовательно, [math]C \setminus z_i \subset \langle A \setminus y_i \rangle [/math].
- По свойствам замыкания 1 и 3 получаем:
[math]C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle[/math]
Так как [math]z_i \in \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle[/math], то [math]A \setminus y_i \cup z_i \notin I[/math], то есть в [math]G_M(A)[/math] не существует ребра [math]\langle y_i, z_i \rangle[/math].
- Но тогда, как было отмечено ранее, не существует полного паросочетания. Получили противоречие.
|
| [math]\triangleleft[/math] |
См. такжеИсточники информации