Коды Прюфера

Алгоритм построения кодов Прюфера

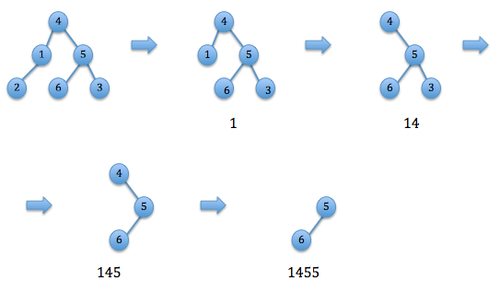
Кодирование Прюфера переводит помеченные деревья порядка [math]n[/math] в последовательность чисел от [math]1[/math] до [math]n[/math] по алгоритму:
Пока количество вершин больше двух:

1. Выбирается лист [math]v[/math] с минимальным номером.
2. В код Прюфера добавляется номер вершины, смежной с [math]v[/math].
3. Вершина [math]v[/math] и инцидентное ей ребро удаляются из дерева.

Полученная последовательность называется кодом Прюфера (англ. Prüfer code) для заданного дерева.

Лемма:

Номер вершины [math]v[/math] встречается в коде Прюфера тогда и только тогда, когда [math]v[/math] не является листом, причём встречается этот номер к коде дерева в точности [math]\deg v - 1[/math] раз.

Доказательство:

[math]\triangleright[/math]

Вершина с номером [math]n[/math] не может быть удалена, следовательно на последнем шаге у неё была смежная вершина, и число [math]n[/math] встретилось в коде. Если вершина не является листом, то у неё на некотором шаге была смежная вершина [math]-[/math] лист, следовательно номер этой вершины встречается в коде. Если вершина является листом с номером меньше [math]n[/math], то она была удалена до того, как был удален её сосед, следовательно её номер не встречается в коде. Таким образом, номера всех вершин, не являющихся листьями или имеющих номер [math]n[/math], встречаются в коде Прюфера, а остальные [math]-[/math] нет.

[math]\triangleleft[/math]

Лемма:

По любой последовательности длины [math]n - 2[/math] из чисел от [math]1[/math] до [math]n[/math] можно построить помеченное дерево, для которого эта последовательность является кодом Прюфера.

Доказательство:

[math]\triangleright[/math]

Доказательство проведем по индукции по числу [math]n[/math] База индукции: [math]n = 1[/math] [math]-[/math] верно. Индукционный переход: Пусть для числа [math]n[/math] верно, построим доказательство для [math]n+1[/math]: Пусть у нас есть последовательность: [math]A = [a_1, a_2, ..., a_{n - 2}].[/math] Выберем минимальное число [math]v[/math] не лежащее в [math]A[/math]. По предыдущей лемме [math]v[/math] [math]-[/math] вершина, которую мы удалили первой. Соединим [math]v[/math] и [math]a_1[/math] ребром. Выкинем из последовательности [math]A[/math] число [math]a_1[/math]. Перенумеруем вершины, для всех [math]a_i \gt v[/math] заменим [math]a_i[/math] на [math]a_i - 1[/math]. А теперь мы можем применить предположение индукции.

[math]\triangleleft[/math]

Теорема:

Кодирование Прюфера задаёт биекцию между множествами помеченных деревьев порядка [math]n[/math] и последовательностями длиной [math]n - 2[/math] из чисел от [math]1[/math] до [math]n[/math]

Доказательство:

[math]\triangleright[/math]

Каждому помеченному дереву приведенный алгоритм сопоставляет последовательность. Каждой последовательности, как следует из предыдущей леммы, соотвествует помеченное дерево.

[math]\triangleleft[/math]

Следствием из этой теоремы является формула Кэли.

Пример построения кода Прюфера

Алгоритм декодирования кодa Прюфера

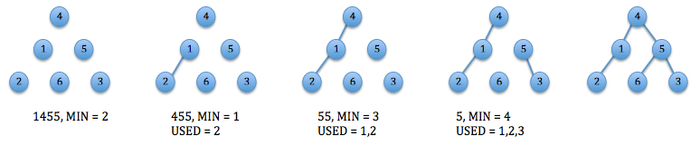
В массиве вершин исходного дерева [math]V[/math] найдём вершину [math]v_{min}[/math] с минимальным номером, не содержащуюся в массиве с кодом Прюфера [math]P[/math], т.е. такую, что она является листом или концом уже добавленного в граф ребра, т.е. она стала листом в процессе построения кода Прюфера (по первому пункту построения). Вершина [math]p_1[/math] была добавлена в код Прюфера как инцидентная листу с минимальным номером (по второму пункту построения), поэтому в исходном дереве существует ребро {[math]p_1[/math], [math]v_{min}[/math]}, добавим его в список ребер. Удалим первый элемент из массива [math]Р[/math], а вершину [math]v_{min}[/math] - из массива [math]V[/math] т.к. она больше не может являться листом (по третьему пункту построения). Будем выполнять вышеуказанные действия, пока массив [math]P[/math] не станет пустым. В конце работы алгоритма в массиве [math]V[/math] останутся две вершины, составляющие последнее ребро дерева (это следует из построения).

Реализация

# P - код Прюфера
# V - вершины
function buildTree(P, V):
   while not P.empty():
      u = P[0]
      v = min(x [math]\in[/math] V: P.count(x) == 0)
      G.push({u, v})
      P.erase(0)
      V.erase(indexOf(v))
   G.push({v[0], v[1]})
   return G

Пример декодирования кода Прюфера

См. также

• Связь матрицы Кирхгофа и матрицы инцидентности
• Матрица Кирхгофа
• Количество помеченных деревьев
• Подсчет числа остовных деревьев с помощью матрицы Кирхгофа

Источники информации

• Университет INTUIT | Представление с помощью списка ребер и кода Прюфера