Дерево Фенвика — различия между версиями
Shersh (обсуждение | вклад) м (→Построение дерева) |
|||
| Строка 115: | Строка 115: | ||
modify(i, d) | modify(i, d) | ||
| + | ==Построение дерева== | ||
| + | Будем строить дерево Фенвика исходя из его описания. Можно заметить, что <tex>T_{i}</tex> можно считать быстрее, чем по формуле <tex> T_i = \sum\limits_{k = F(i)}^{i} a_k</tex>. Мы можем представить <tex>T_{i}</tex> как сумму нескольких элементов дерева с меньшими индексами и <tex>a_i</tex> (например, <tex>T_{7} = a_{7} + T_{6} + T_{5} + T_{3}</tex>). Рассмотрим, как получается эта сумма. Элемент <tex>a_i</tex> не учитывался в предыдущих суммах, поэтому мы его прибавляем к <tex>T_i</tex>. <tex>a_{i-1}</tex> содержится только в <tex>T_{i-1}</tex>, поэтому прибавим <tex>T_{i-1}</tex>. Так как <tex>T_{i-1}</tex> может состоять из нескольких элементов из <tex>A</tex>, то мы пропустим все такие <tex>T_j</tex>, которые содержат элементы из <tex>T_{i-1}</tex>. Мы знаем, что <tex>T_j</tex> содержит <tex>a_j</tex>, поэтому можно пропустить все такие <tex>T_j</tex>, где <tex>j</tex> входит в диапазон от <tex>F(i - 1)</tex> до <tex>i - 2</tex> (индексы элементов <tex>T_{i-1}</tex>). | ||
| + | |||
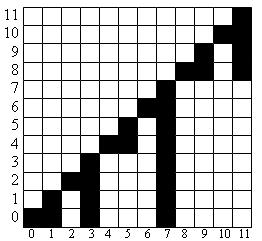
| + | Другими словами, представим каждый элемент массива <tex>T</tex> как столбик (см. картинку). К <tex>a_i</tex> элементу прибавляем <tex>T_{i-1}</tex>. Далее прибавляем такой столбик, верхняя граница которого находится на том же уровне, что нижняя граница предыдущего прибавляемого столбика. Прекращаем складывать, когда нижняя граница нового столбика будет равна <tex>F(i)</tex>. | ||
| + | |||
| + | Покажем, что если мы прибавили столбик, то <tex>F(i) \leqslant F(j)</tex>, то его нижняя граница не ниже, чем нижняя граница столбика <tex>T_i</tex>. Прибавление столбика возможно при условии <tex>F(i) \leqslant j \leqslant i</tex>. Это значит, что отбросив количество цифр, равное количеству последних единиц у числа <tex> i </tex>, из конца двоичной записи <tex>F(i)</tex>, <tex>j</tex> и <tex> i</tex>, то мы получим равные числа. Тогда <tex>F(j)</tex> не может быть меньше <tex>F(i)</tex>. | ||
| + | |||
| + | '''function''' init(i) | ||
| + | t[i] = a[i] | ||
| + | j = i - 1 | ||
| + | '''while''' j >= F(i) | ||
| + | t[i] += t[j] | ||
| + | j = F(j) - 1 | ||
| + | |||
| + | Такое построение будет работать за <tex>O(n \log{n})</tex>. | ||
== Запрос получения значения функции на префиксе == | == Запрос получения значения функции на префиксе == | ||
Пусть существует некоторая бинарная операция <tex>\circ</tex>. Чтобы получить значение на отрезке <tex>[i, j]</tex>, нужно провести операцию, обратную к <tex>\circ</tex>, над значениями на отрезках <tex>[0, j]</tex> и <tex>[0, i - 1]</tex>. | Пусть существует некоторая бинарная операция <tex>\circ</tex>. Чтобы получить значение на отрезке <tex>[i, j]</tex>, нужно провести операцию, обратную к <tex>\circ</tex>, над значениями на отрезках <tex>[0, j]</tex> и <tex>[0, i - 1]</tex>. | ||
| Строка 122: | Строка 137: | ||
Обозначим <tex> G_i = \mathrm sum(i) = \sum\limits_{k = 0}^{i} a_k </tex>. Тогда <tex> \mathrm sum(i, j) = \sum\limits_{k = i}^{j} a_k = G_j - G_{i - 1} </tex>. | Обозначим <tex> G_i = \mathrm sum(i) = \sum\limits_{k = 0}^{i} a_k </tex>. Тогда <tex> \mathrm sum(i, j) = \sum\limits_{k = i}^{j} a_k = G_j - G_{i - 1} </tex>. | ||
| − | + | Мы можем найти сумму аналогично построению дерева. Будем складывать частичные суммы, пока не дойдем до элемента <tex>a_0</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Реализация === | === Реализация === | ||
| − | |||
Приведем код функции <tex> \mathrm sum(i) </tex>: | Приведем код функции <tex> \mathrm sum(i) </tex>: | ||
'''int''' sum(i): | '''int''' sum(i): | ||
| Строка 146: | Строка 147: | ||
i = f(i) - 1 | i = f(i) - 1 | ||
'''return''' result | '''return''' result | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Сравнение дерева Фенвика и дерева отрезков== | ==Сравнение дерева Фенвика и дерева отрезков== | ||
Версия 14:52, 5 июня 2015
Содержание
Описание структуры
Дерево Фе́нвика (англ. Binary indexed tree) — структура данных, требующая памяти и позволяющая эффективно (за ) выполнять следующие операции:
- изменять значение любого элемента в массиве,
- выполнять некоторую ассоциативную, коммутативную, обратимую операцию на отрезке .
Впервые описано Питером Фенвиком в 1994 году.
Пусть дан массив . Деревом Фенвика будем называть массив из элементов: , где и — некоторая функция, от выбора которой зависит время работы операций над деревом. Рассмотрим функцию, позволяющую делать операции вставки и изменения элемента за время . Она задается простой формулой: , где — это операция побитового логического . При числа и его значения, увеличенного на единицу, мы получаем это число без последних подряд идущих единиц.
Эту функцию можно вычислять по другой формуле: где — количество подряд идущих единиц в конце бинарной записи числа . Оба варианта равносильны, так как функция, заданная какой-либо из этих формул, заменяет все подряд идущие единицы в конце числа на нули.
Запрос изменения элемента
Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Рассмотрим как изменяется массив при изменении элемента .
| Лемма: |
Для пересчёта дерева Фенвика при изменении величины необходимо изменить элементы дерева , для индексов которых верно неравенство . |
| Доказательство: |
| необходимо менять те , для которых попадает в необходимые удовлетворяют условию . |
| Лемма: |
Все такие , для которых меняется при изменении , можно найти по формуле , где — это операция побитового логического . |
| Доказательство: |
| Из доказанной выше леммы следует, что первый элемент последовательности само . Для него выполняется равенство, так как . По формуле мы заменим первый ноль на единицу. Неравенство при этом сохранится, так как осталось прежним или уменьшилось, а увеличилось. не может увеличится, так как функция заменяет последние подряд идущие единицы числа на нули, а по формуле у нового значения увеличивается количество единиц в конце, что не может привести к увеличению . Докажем от противного, что нельзя рассматривать значения , отличные от тех, которые мы получили по формуле. Рассмотрим две различные последовательности индексов. Первая последовательность получена по формуле, вторая — некоторая последовательность чисел, не превосходящие . Возьмём число из второй последовательности, которого нет в первой последовательности. Пусть . Уберём у все подряд идущие единицы в конце двоичной записи, столько же цифр уберём в конце числа . Обозначим их как и . Чтобы выполнялось условие , должно выполняться неравенство . Но если , то и , что противоречит условию . Значит, . Но тогда возможно получить по формуле , следовательно, . Получили противоречие: можно вычислить по формуле, а это значит, что оно содержится в первой последовательности. Таким образом, нужные элементы можно искать по формуле . |
Заметим, что возрастает немонотонно. Поэтому нельзя просто перебирать значения от , пока не нарушается условие. Например, пусть . При данной стратегии на следующем шаге () нарушится условие и мы прекратим пересчитывать . Но тогда мы упускаем остальные значения , например .
| , десятичная запись | |||||||||||
| , двоичная запись | |||||||||||
| , двоичная запись | |||||||||||
| , десятичная запись |
Все мы можем получить следующим образом: . Следующим элементом в последовательности будет элемент, у которого первый с конца ноль превратится в единицу. Можно заметить, что если к исходному элементу прибавить единицу, то необходимый ноль обратится в единицу, но при этом все следующие единицы обнулятся. Чтобы обратно их превратить в единицы, применим операцию . Таким образом все нули в конце превратятся в единицы и мы получим нужный элемент. Для того, чтобы понять, что эта последовательность верна, достаточно посмотреть на таблицу.
Несложно заметить, что данная последовательность строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа .
Можно написать функцию получения .
int next(i): return i = i | (i + 1)
Напишем функцию, которая будет прибавлять к элементу число , и при этом меняет соответствующие частичные суммы. Так как наш массив содержит элементов, то мы будем искать до тех пор, пока оно не превышает значение .
function modify(i, d):
while i < N
t[i] += d
i = next(i);
Часто можно встретить задачу, где требуется заменить значение элемента на . Заметим, что если вычислить разность и , то можно свести эту задачу к операции прибавления к .
function set(i, t): d = t - a[i] modify(i, d)
Построение дерева
Будем строить дерево Фенвика исходя из его описания. Можно заметить, что можно считать быстрее, чем по формуле . Мы можем представить как сумму нескольких элементов дерева с меньшими индексами и (например, ). Рассмотрим, как получается эта сумма. Элемент не учитывался в предыдущих суммах, поэтому мы его прибавляем к . содержится только в , поэтому прибавим . Так как может состоять из нескольких элементов из , то мы пропустим все такие , которые содержат элементы из . Мы знаем, что содержит , поэтому можно пропустить все такие , где входит в диапазон от до (индексы элементов ).
Другими словами, представим каждый элемент массива как столбик (см. картинку). К элементу прибавляем . Далее прибавляем такой столбик, верхняя граница которого находится на том же уровне, что нижняя граница предыдущего прибавляемого столбика. Прекращаем складывать, когда нижняя граница нового столбика будет равна .
Покажем, что если мы прибавили столбик, то , то его нижняя граница не ниже, чем нижняя граница столбика . Прибавление столбика возможно при условии . Это значит, что отбросив количество цифр, равное количеству последних единиц у числа , из конца двоичной записи , и , то мы получим равные числа. Тогда не может быть меньше .
function init(i)
t[i] = a[i]
j = i - 1
while j >= F(i)
t[i] += t[j]
j = F(j) - 1
Такое построение будет работать за .
Запрос получения значения функции на префиксе
Пусть существует некоторая бинарная операция . Чтобы получить значение на отрезке , нужно провести операцию, обратную к , над значениями на отрезках и .
В качестве бинарной операции рассмотрим операцию сложения.
Обозначим . Тогда .
Мы можем найти сумму аналогично построению дерева. Будем складывать частичные суммы, пока не дойдем до элемента .
Реализация
Приведем код функции :
int sum(i):
result = 0;
while i >= 0
result += t[i]
i = f(i) - 1
return result
Сравнение дерева Фенвика и дерева отрезков
- Дерево Фенвика занимает в константное значение раз меньше памяти, чем дерево отрезков. Это следует из того, что дерево Фенвика хранит только значение операции для каких-то элементов, а дерево отрезков хранит сами элементы и частичные результаты операции на подотрезках, поэтому оно занимает как минимум в два раза больше памяти.
- Дерево Фенвика проще в реализации.
- Операция на отрезке, для которой строится дерево Фенвика, должна быть обратимой, а это значит, что минимум (как и максимум) на отрезке это дерево считать не может, в отличие от дерева отрезков. Но если нам требуется найти минимум на префиксе, то дерево Фенвика справится с этой задачей. Такое дерево Фенвика поддерживает операцию уменьшения элементов массива. Пересчёт минимума в дереве происходит быстрее, чем обновление массива минимумов на префиксе.