Обучение в реальном времени
Обучение в реальном времени, онлайн-обучение (англ. online machine learning) — вид машинного обучения, при котором данные поступают в последовательном порядке и используются для обновления лучшего предсказания на каждом шаге.
Общая информация
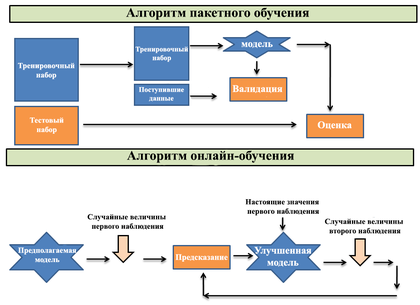
Алгоритмы пакетного обучения обладают рядом критических недостатков из-за необходимости обучать модель с нуля при получении новых данных: низкая эффективность по времени и памяти, плохая масштабируемость для крупных систем. Онлайн-обучение решает эти проблемы, поскольку модель обновляется на основе поступающих в каждый момент времени данных. Благодаря этому алгоритмы онлайн-обучения гораздо более эффективны в приложениях, где данные не только имеют большой размер, но и поступают с высокой скоростью.
При онлайн-обучении для построения модели необходим один проход по данным, что позволяет не сохранять их для последующего доступа в процессе обучения и использовать меньший объем памяти. Обработка одного объекта за раз также значительно упрощает реализацию алгоритма онлайн-обучения. Однако изменение вида входных данных, выход сервера из строя и многие другие причины могут привести к некорректной работе системы. Оценить качество работы системы при онлайн-обучении сложнее, чем при пакетном: нет возможности получить репрезентативный тестовый набор данных.
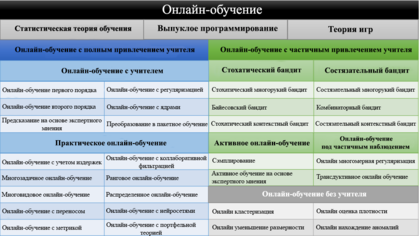
В зависимости от типа обратной связи существующие методы онлайн-обучения можно разделить на три группы:
- Онлайн-обучение с учителем (англ. supervised online learning)
- Онлайн-обучение с частичным привлечением учителя (англ. online learning with limited feedback)
- Онлайн-обучение без учителя (англ. unsupervised online learning)
Математическая основа
Функция ожидаемого риска (англ. Expected Risk Function)
Цель системы обучения состоит в поиске минимума функции , называемой функцией ожидаемого риска.
Переменная минимизации предназначена для представления части системы обучения, которая должна быть адаптирована в качестве реакции на наблюдение событий , происходящих в реальном мире. Функция потерь измеряет производительность системы обучения с параметром при обстоятельствах, описанных событием .
События моделируются как случайные независимые наблюдения, взятые из неизвестного распределения вероятности . Функция риска - это ожидание функции потерь для фиксированного значения параметра .
Функция ожидаемого риска не может быть минимизирована напрямую, потому что распределение неизвестно. Однако возможно вычислить приближение , используя конечный обучающий набор независимых наблюдений .
Пакетный градиентный спуск (англ. Batch Gradient Descent)
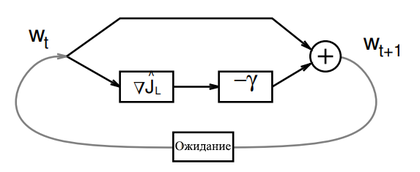
Минимизировать эмпирический риск можно с помощью алгоритма пакетного градиентного спуска. Последовательные оценки оптимального параметра вычисляются по следующей формуле, где - положительное число:
Когда скорость обучения достаточно мала, алгоритм сходится к локальному минимуму эмпирического риска . Значительное ускорение сходимости может быть достигнуто путем замены скорости обучения подходящей положительно определенной матрицей.
Каждая итерация алгоритма пакетного градиентного спуска включает в себя вычисление среднего значения градиентов функции потерь по всей обучающей выборке. Для хранения достаточно большой обучающей выборки и вычисления этого среднего должны быть выделены значительные вычислительные ресурсы и память.
Градиентный спуск в реальном времени (англ. Online Gradient Descent)
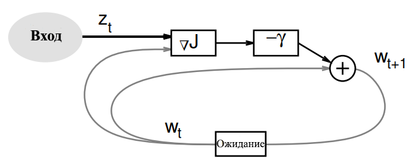
Алгоритм градиентного спуска в реальном времени получается при удалении операции усреднения в алгоритме пакетного градиентного спуска. Вместо усреднения градиента потерь по всей обучающей выборке каждая итерация градиентного спуска в реальном времени состоит из случайного выбора примера и обновления параметра в соответствии со следующей формулой:
Усреднение этого обновления по всем возможным вариантам обучающего примера позволяет восстановить алгоритм пакетного градиентного спуска. Упрощение градиентного спуска в реальном времени основано на предположении, что случайный шум, вносимый этой процедурой, не будет мешать усредненному поведению алгоритма. Эмпирические данные подтверждают это предположение.
Градиентный спуск в реальном времени также может быть описан без использования обучающей выборки, используя события из реального мира напрямую. Такая формулировка подходит для описания адаптивных алгоритмов, обрабатывающих поступающее наблюдение и одновременно обучающихся работать лучше. Такие адаптивные алгоритмы наиболее полезны для отслеживания явлений, развивающихся во времени.
Общий алгоритм градиентного спуска в реальном времени используется для минимизации следующей функции стоимости :
Каждая итерация этого алгоритма состоит из извлечения события из распределения и применения следующей формулы обновления, где - либо положительное число, либо положительно определенная матрица:
удовлетворяет следующему условию:
Примеры
Adaline
Алгоритм обучения Adaline подбирает параметры одного порогового элемента. Входные данные распознаются как класс или в зависимости от знака . Целесообразно рассмотреть расширенный набор входных данных , содержащий дополнительный постоянный коэффициент, равный 1. Смещение тогда представляется как дополнительный коэффициент в векторе параметров . Тогда вывод порогового элемента имеет вид:
Параметр корректируется после использования дельта-правила:
Дельта-правило - это итерация алгоритма градиентного спуска в реальном времени со следующей функцией потерь, где :
Многослойные сети (англ. Multi-Layer Networks)
Многослойные сети были разработаны для преодоления вычислительных ограничений пороговых элементов. Произвольные двоичные отображения могут быть реализованы путем объединения нескольких слоев пороговых элементов, при этом каждый слой использует выходные данные элементов предыдущих слоев в качестве входных данных.
Разрыв порогового элемента может быть представлен плавным нелинейным приближением:
Использование таких сигмоидальных элементов не уменьшает вычислительные возможности многослойной сети.
Многослойная сеть сигмоидальных элементов реализует дифференцируемую функцию от входных данных и параметров . Алгоритм обратного распространения ошибки обеспечивает эффективный способ вычисления градиентов функции среднего квадрата потерь.
K-Means
Алгоритм K-Means можно получить, выполнив градиентный спуск в реальном времени со следующей функцией потерь:
Эта функция потерь измеряет ошибку в положении точки , когда мы заменяем ее ближайшим центроидом, и удовлетворяет следующему условию:
Поэтому можно игнорировать недифференцируемые точки и применять алгоритм градиентного спуска в реальном времени.