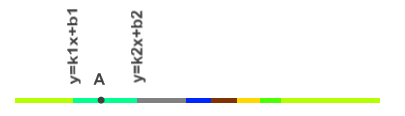Персистентные структуры данных — различия между версиями
(→Получение полностью персистентных структур данных) |
|||
| Строка 74: | Строка 74: | ||
[[Файл:Полная персистентность.png]] | [[Файл:Полная персистентность.png]] | ||
| − | Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции ''«insert after»'' и ''«order»''. Обе операции нужно делать за <tex>O(1</tex> | + | Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции ''«insert after»'' и ''«order»''. Обе операции нужно делать за <tex>O(1)</tex>. Это список с поддержкой запроса о порядке ''List Order Maintenance'' <ref>[http://www.cs.au.dk/~gerth/aa11/slides/order.pdf]</ref>. |
Операция обновления в этом списке будет происходить так: в список версий добавляется два элемента — первый вносит изменение, а второй будет возвращать обратно значение предыдущей версии. Таким образом, каждая операция разбивается на две: первая делает изменение, а вторая его откатывает. | Операция обновления в этом списке будет происходить так: в список версий добавляется два элемента — первый вносит изменение, а второй будет возвращать обратно значение предыдущей версии. Таким образом, каждая операция разбивается на две: первая делает изменение, а вторая его откатывает. | ||
В ''change log'' «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут отсортированы по их порядку в списке версий с помощью ''List Order Maintenance''. | В ''change log'' «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут отсортированы по их порядку в списке версий с помощью ''List Order Maintenance''. | ||
Версия 22:24, 5 апреля 2015
| Определение: |
| Персистенные структуры данных — это структуры данных, которые при внесении в них каких-то изменений сохраняют все свои предыдущие состояния и доступ к этим состояния. |
Содержание
- 1 Уровни персистентности
- 2 Способы преобразования структур данных в персистентные
- 3 Преобразование списка в персистентный за O(1)
- 4 Общий метод построения частично персистентных структур данных
- 5 Получение полностью персистентных структур данных
- 6 Использование персистентных структур данных для решения геометрических задач
- 7 См. также
- 8 Примечания
- 9 Источники информации
Уровни персистентности
Есть несколько уровней персистентности
- частичная (англ. partial)
- полная (англ. full)
- конфлюэнтная (англ. confluent)
- фунциональная (англ. functional)
В частично персистентных структурах данных к каждой версии можно делать запросы, но изменять можно только последнюю версию структуры данных.
В полностью персистентных структурах данных можно менять не только последнюю, но и любую версию структур данных, также к любой версии можно делать запросы.
Конфлюэнтные структуры данных позволяют объединять две структуры данных в одну (деревья поиска, которые можно сливать).
Функциональные структуры данных полностью персистентны по определению, так как в них запрещаются уничтожающие присваивания, т.е. любой переменной значение может быть присвоено только один раз и изменять значения переменных нельзя. Если структура данных функциональна, то она и конфлюэнтна, если конфлюэнтна, то и полностью персистентна, если полностью персистентна, то и частично персистентна. Однако бывают структуры данных не функциональные, но конфлюэнтные.
Способы преобразования структур данных в персистентные
Есть несколько способов сделать любую структуру персистентной:
- полное копирование (англ. full copy) когда при любой операции изменения полностью копируется структура данных и в получившуюся новую копию вносятся изменения;
- копирование пути (англ. path copiyng);
- метод «толстых» узлов (англ. fat node).
Рассмотрим для начала частичную персистентность. Для наглядности занумеруем разные версии структур данных. История изменений структуры данных линейна, мы в любой момент времени можем обратиться к любой версии структуры данных, но поменять можем только последнюю версию.
Сформулируем, что такое структура данных. Это набор узлов, в которых хранятся какие-то данные и эти узлы связаны ссылками. Классический пример структуры данных — дерево. Рассмотрим, как методом копирования пути превратить дерево в персистентное.
Метод копирование пути
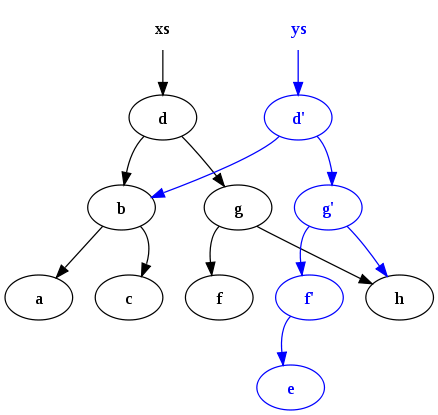
Пусть нам нужно сделать какое-то обновление в дереве, например, добавить очередной элемент, но при этом мы не хотим потерять старое дерево. Возьмем узел, в который мы хотим добавить нового ребенка. Вместо того чтобы добавлять нового ребенка, мы скопируем этот узел, к копии добавим нового ребенка, также скопируем все узлы вплоть до корня, из которых достижим первый скопированный нами узел вместе со всеми указателями. Все вершины, из которых наш измененный узел не достижим, мы не трогаем.
Метод «толстых» узлов
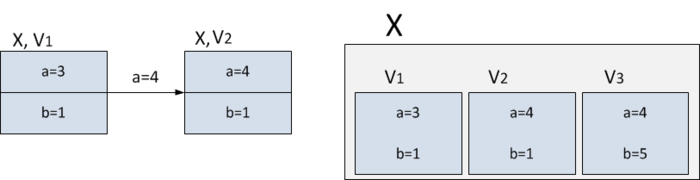
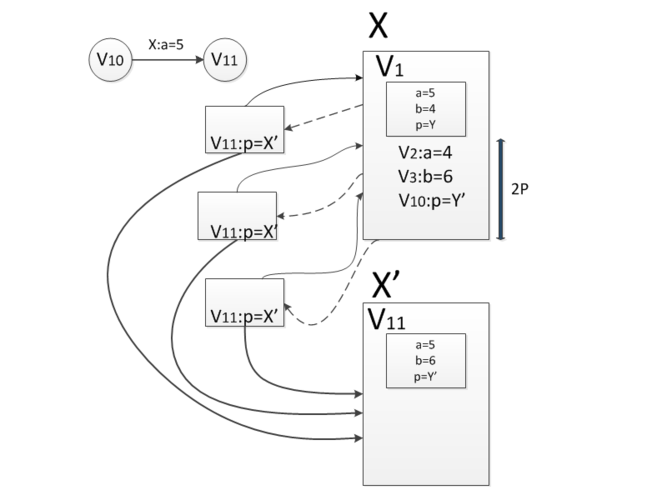
Пусть в структуре данных есть узел, в котором нужно сделать изменения (например, на нашем рисунке в первой версии структуры данных есть поле , а во второй версии это поле должно быть равно ), но при этом нужно сохранить доступ и к старой версии узла. В таком случае можно хранить их оба в большом комбинированном узле.
В нашем примере в этом «толстом» узле будет храниться первая версия , у которой и вторая версия , у которой . Если далее последуют еще какие-то изменения (например, поле нашего узла станет равно ) сделаем еще одну версию структуры данных — . Чтобы быстро найти нужную версию в списке версий, хранящихся в «толстом» узле, нужно хранить их в виде дерева. Тогда мы сможем за логарифм найти нужную версию и к ней обратиться. Значит все операции, которые будут производиться на этой структуре данных, будут домножаться на логарифм от числа версий.
Преобразование списка в персистентный за O(1)
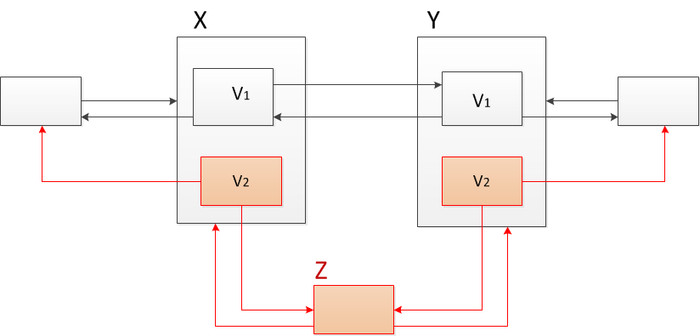
Если скомбинировать методы path copiyng и fat node, то получим универсальный метод, который позволит преобразовывать структуры данных в частично персистентные без дополнительного логарифма памяти. Пусть мы имеем двусвязный список и хотим внести в него какое-то изменение, например, добавить узел между узлами и , то есть при переходе из версии в версию добавим в двусвязный список узел . Применим метод «толстых» узлов. Для этого в узлы и добавим вторую версию и изменим ссылку, следующую из , и предыдущую перед , как показано на рисунке. Эта структура работает так. Например, мы знаем, что текущая первая версия и идем по нашему списку слева направо от первого узла к узлу , а затем хотим перейти к следующему узлу. В «толстом» узле мы выбираем нужную нам версию и далее следуем по ссылкам.
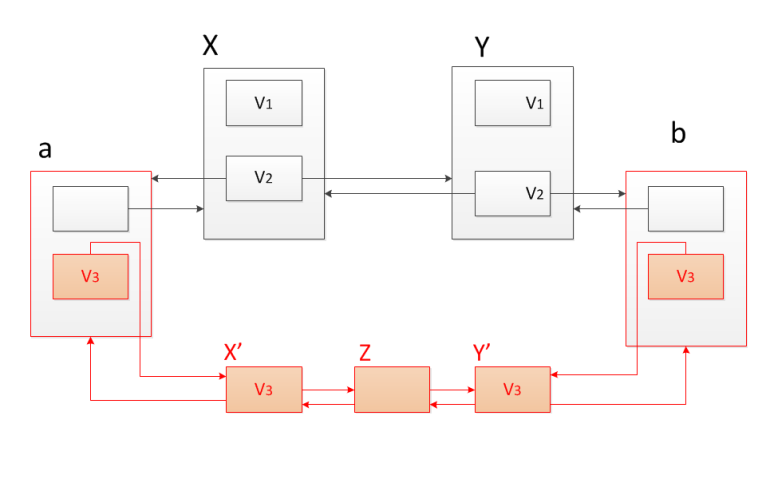
Пусть мы хотим добавить еще один элемент между узлами и , но проблема в том, что у и уже есть вторая версия, добавлять третью невыгодно. Поэтому более двух версий добавлять не будем. Используем метод копирования пути. Скопируем узлы и , начиная с их третьей версии, и свяжем новые узлы с исходным списком. Для этого добавим вторые версии предыдущему перед и последующему после узлам и свяжем эти узлы соответствующими ссылками. Так все версии остаются доступными.
Будем называть узел полным, если у него есть вторая версия. Если мы хотим вставить новый элемент в середину списка, мы должны склонировать все полные узлы слева и справа от места добавления нового узла, дойти до ближайших элементов, у которых нет второй версии и добавить им вторую версию.
Оценим амортизационное время работы такого алгоритма. У нас частично персистентная структура данных, мы изменяем только ее последнюю версию. Примем функцию потенциала равной числу полных узлов в последней версии. Если мы склонировали узлов, то количество полных узлов в последней версии уменьшится на , и еще два узла мы добавим (по одному слева и справа). Таким образом, амортизационное время работы по добавлению элемента будет .
Общий метод построения частично персистентных структур данных
Применим методы, описанные выше, в общем случае для абстрактной структуры данных. Пусть есть структура данных, у каждого узла которой количество указателей на этот узел не больше некоторой константы . Если мы будем клонировать узел, нам важно будет знать, откуда на этот узел идут указатели, чтобы затем их переставить. Поэтому будем в каждом узле хранить обратные ссылки на те узлы, которые ссылаются на клонируемый нами узел. Все узлы будем хранить в виде «толстых» узлов, в которых содержится начальная версия этого узла и список внесенных в него изменений (англ. change log) длиной не больше . Пусть мы хотим внести изменение в нашу структуру данных в узел . Если у нас есть место в списке изменений, мы просто вносим наше изменение туда. Если change log заполнен, то мы клонируем узел : берем стартовую версию узла, производим в ней все изменения, записанные в change log, добавляем последнее изменение и делаем версию со свободным списком изменений. Затем пройдем по обратным ссылкам от и в change log каждого узла, ссылающегося на , добавим изменение указателя начиная с этой версии структуры данных с на .
Оценим время работы этого алгоритма. Введем функцию потенциала, которая будет равна суммарному размеру всех списков изменений в последней версии. Посмотрим, как меняется суммарный размер списков изменений, когда мы совершаем одно изменение. Если change log был не полный, то мы просто добавляем туда один элемент, потенциал увеличится на единицу. Если change log был полный, то потенциал уменьшается на его размер, так как мы склонировали узел с пустым списком изменений. После этого мы пошли по обратным ссылкам (их было штук) и добавили в узлов по одному значению. Таким образом амортизированное время работы будет .
Получение полностью персистентных структур данных
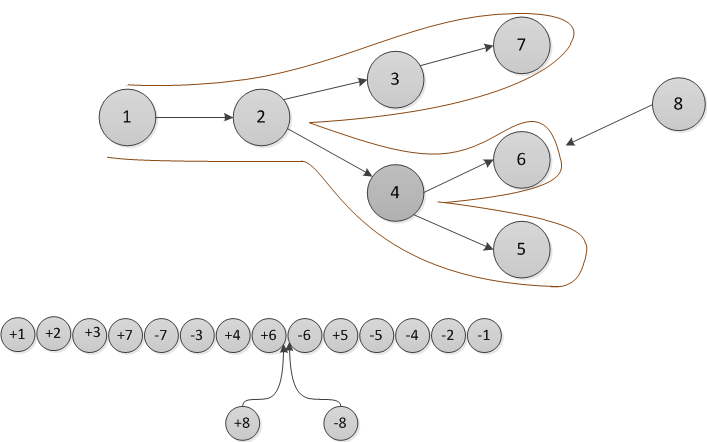
Для полностью персистентных структур данных применить описанный выше метод преобразования не получится, так как история создания версий не линейна и нельзя отсортировать изменения по версиям, как в частично персистентных структурах данных. Пусть мы храним историю изменения версий в виде дерева. Сделаем обход этого дерева в глубину. В порядке этого обхода запишем, когда мы входим, а когда выходим из каждой версии. Эта последовательность действий полностью задает дерево, сделаем из нее список. Когда добавляется новая версия нашей структуры данных, мы вставляем два элемента в середину списка.
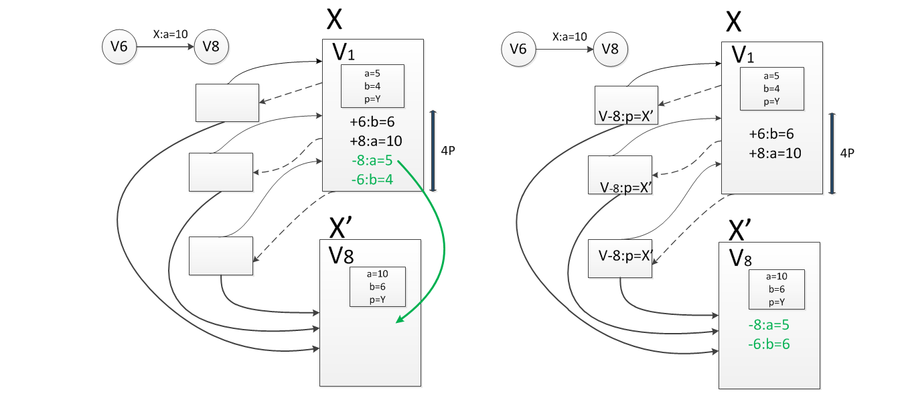
Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции «insert after» и «order». Обе операции нужно делать за . Это список с поддержкой запроса о порядке List Order Maintenance [1]. Операция обновления в этом списке будет происходить так: в список версий добавляется два элемента — первый вносит изменение, а второй будет возвращать обратно значение предыдущей версии. Таким образом, каждая операция разбивается на две: первая делает изменение, а вторая его откатывает. В change log «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут отсортированы по их порядку в списке версий с помощью List Order Maintenance. В какой-то момент change log «толстого» узла переполнится. Тогда нужно клонировать этот узел и нижнюю половину изменений перенести в change log склонированного узла. Первую половину изменений применяем к исходной версии узла и сохраняем в качестве исходной в склонированном узле.
Получится два узла: первый отвечает за отрезок версий до операции последнего изменения, а второй после нее. Дальнейший порядок действий аналогичен тому, который использовался в общем методе построения частично персистентных структур данных.
Оценим амортизационное время работы этого алгоритма. Введем потенциал, равный суммарному размеру нижних половин списков изменений во всех версиях. Когда мы раздваиваем узел, мы уменьшаем потенциал на половину размера списка изменений (в нашем примере это ), затем мы переставляем ссылок, потенциал увеличивается на , значит амортизационное время работы — .
Использование персистентных структур данных для решения геометрических задач
Персистентные структуры данных используются при решении геометрических задач. Примером может служить Point loctaion problem — задача о местоположении точки. Задачи такого рода решаются в offline и online. В offline-задачах все запросы даны заранее и можно обрабатывать их одновременно. В online-задачах следующий запрос можно узнать только после того, как найден ответ на предыдущий.
Сначала рассмотрим решение offline-задачи. Пусть дан набор многоугольников, они не пересекаются, но могут иметь общие вершины, суммарное число вершин — . Запрос: точка . Вернуть нужно многоугольник, в котором она находится. Количество точек .
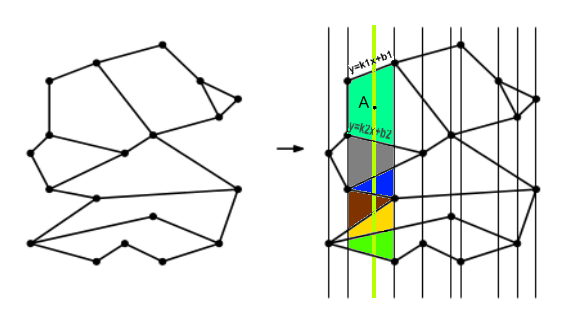
Через каждую вершину всех многоугольников проведем вертикальные прямые. Вся плоскость будет разбита на полосы. Внутри полос находится набор трапеций и треугольников, высеченных из многоугольников. Если посмотреть каждую из этих фигур слева направо, то это будет набор расширяющихся или сужающихся отрезков.
Используем технику, которая называется сканирующей прямой (scane line). Возьмем вертикальную прямую и направим ее из минус бесконечности в плюс бесконечность. Пусть она движется перпендикулярно себе по заданным нам многоугольникам. Порядок расположения отрезков, принадлежащих разным многоугольникам, задан однозначно. Возьмем точки, которые являются точками пересечения сканирующей прямой с границами многоугольников.
Сведем задачу к одномерной. Прямая проходит через точку . Для того, чтобы найти в каком отрезке лежит эта точка, нужно точки-границы отрезков хранить отсортированными по возрастанию и найти между какими двумя точками лежит точка . Это можно сделать бинпоиском. Если этот отрезок принадлежит какому-то из данных многоугольников, то значит и точка лежит внутри этого многоугольника.
Построим сбалансированное дерево поиска, в котором будем хранить точки, которые являются границами отрезков, но не в виде чисел, а как линейные функции вида . Для каждой вершины дерева ее ключ — это линейная функция. При переходе из одной полосы в другую будем обрабатывать события. Это могут быть операции добавления, удаления, замены элементов в дерево. Чтобы найти точку внутри полосы будем подставлять -координату точки-запроса в линейные функции и найдем в двоичном дереве место, где находится точка, затем определим, в каком многоугольнике лежит точка-запрос.
Итого обрабатывается n событий, каждое за и запросов, также каждый за . Общее время работы алгоритма .
При решении online-задачи вместо обычного двоичного дерева нужно поддерживать частично персистентное дерево. Будем идти слева направо и поддерживать персистентное дерево поиска. Тогда для каждой полосы у нас будет своя версия дерева.
Пусть приходит online-запрос. Двоичным поиском найдем, в какой полосе находится точка. Далее делаем запрос к версии дерева, соответствующей этой полосе и получаем ответ. Итого для решения задачи нужно препроцессинга и на запрос.