Триангуляция Делоне
Определение
| Определение: |
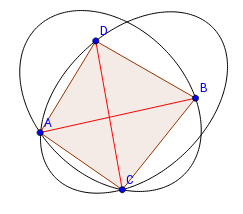
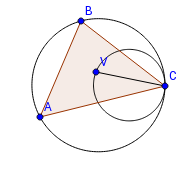
| Подразбиение Делоне множества точек — такое разбиение выпуклой оболочки множества точек на множество выпуклых фигур, что в окружности, описанной вокруг любой из фигур, не находится никаких точек из множества. |
| Определение: |
| Триангуляция Делоне множества точек — триангуляция, являющаяся подразбиением Делоне. |
Существование триангуляции Делоне
| Лемма (1): |
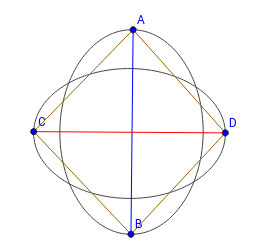
Окружность, спроецированная на параболоид, находится в одной плоскости. Все точки, лежащие внутри окружности, будут лежать под этой плоскостью. Точки, лежащие вне окружности, будут лежать над плоскостью. |
| Доказательство: |
|
Рассмотрим окружность с центром в точке радиуса , она описывается уравнением: . Раскрывая скобки в уравнении окружности, получим Рассмотрим параболоид, пускай его уравнение имеет вид . При проецировании, для проекции окружности на параболоид верны оба уравнения: и окружности, и параболоида, поэтому в уравнение окружности вместо можно подставить , получится Заметим, что получившееся уравнение является уравнением плоскости: , то есть, все точки проекции окружности будут лежать в одной плоскости. Рассмотрим любую точку внутри данной окружности. Через нее можно провести окружность с центром в точке и радиусом , тогда плоскость, проходящая через проекцию этой окружности на параболоид будет иметь уравнение , то есть, обе плоскости будут параллельны и вторая плоскость будет лежать под плоскостью окружности (поскольку , то ). Аналогично доказывается, что точки лежащие вне окружности лежат над плоскостью. |
| Теорема: |
Подразбиение Делоне существует, причём для каждого набора точек оно единственно. |
| Доказательство: |
|
Спроецируем все точки на параболоид и построим выпуклую оболочку. Все грани выпуклой оболочки окажутся внутри параболоида из-за его выпуклости. При этом точки лежат на параболоиде. Поэтому не найдётся точек, которые будут лежать за гранями выпуклой оболочки. То есть все точки, спроецированные на параболоид, будут принадлежать выпуклой оболочке. По лемме 1 очевидно, что внутри окружностей, описанных вокруг проекций граней выпуклой оболочки, не будет лежать никаких точек. Значит, проекции граней — фигуры подразбиения Делоне. Значит, такое подразбиение существует. Из единственности выпуклой оболочки следует, что такое подразбиение единственно. |
Критерий Делоне для рёбер
| Определение: |
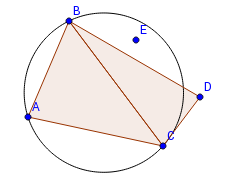
| Критерий Делоне для ребра: на ребре можно построить такую окружность, что внутри неё не будет лежать никаких точек. |
| Лемма (2): |
Триангуляции Делоне принадлежат те и только те рёбра (с поправкой на точки, лежащие на одной окружности), которые удовлетворяют критерию Делоне. |
| Доказательство: |
|
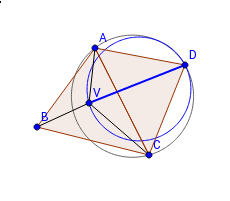
То, что для рёбер, принадлежащих триангуляции Делоне, выполняется критерий Делоне для рёбер, очевидно (вокруг каждого ребра можно описать окружность, проходящую через противолежащую ему точку в смежном треугольнике, причём в окружности не будет никаких точек по критерию Делоне). Докажем, что если для ребра выполняется критерий Делоне, то оно принадлежит триангуляции Делоне. Предположим, что это ребро (назовём его ) не принадлежит триангуляции Делоне. Тогда существует пересекающее его ребро , принадлежащее триангуляции. Рассмотрим четырёхугольник . Точки и лежат вне окружности, построенной на как на хорде, поэтому сумма углов и меньше 180°. Аналогичным образом доказывается, что сумма углов и тоже меньше 180°. Значит, сумма углов четырёхугольника меньше 360°, что невозможно. Противоречие. Значит, ребро принадлежит триангуляции Делоне. |
Локальный критерий Делоне
| Определение: |
| Локальный критерий Делоне для ребра: для пары треугольников, которым принадлежит это ребро, выполняется критерий Делоне (то есть вершина, противолежащая ребру в одном треугольнике, не лежит в окружности, описанной вокруг другого, и наоборот). |
Будем называть хорошими те рёбра, для которых выполняется локальный критерий Делоне.
| Лемма (3): |
Из двух рёбер, которые можно провести для пары треугольников, как минимум одно хорошее. |
| Доказательство: |
| Предположим, что это не так, то есть оба ребра (назовём их и ) плохие. Рассмотрим четырёхугольник и окружность, описанную вокруг треугольника . Точка лежит внутри этой окружности, значит, сумма углов и больше 180°. Аналогично доказывается, что сумма углов и больше 180°. Значит, сумма углов четырёхугольника больше 360°, что невозможно. |
| Лемма (4): |
Если для всех рёбер выполняется локальный критерий Делоне, то выполняется и глобальный критерий Делоне. |
| Доказательство: |
|
Предположим, что это не так, то есть все рёбра хорошие, но существуют треугольники, описанная окружность которых содержат какие-либо точки триангуляции. Возьмём какую-либо конфликтную точку . Рассмотрим такой треугольник из тех, в описанную окружность которых попадает , что угол максимален, если — ближайшая к точке сторона. Пусть треугольник — смежный с . Докажем, что точка лежит в окружности, описанной вокруг . Предположим, что это не так. Посмотрим на окружность, описанную вокруг треугольника : и . Если точка не лежит в окружности, описанной вокруг треугольника , то , что противоречит предыдущим двум неравенствам. Очевидно, что угол больше, чем угол . При этом точка лежит в окружности, описанной вокруг . Значит, при выборе треугольника нужно было взять не , а . Противоречие. |
Динамическая триангуляция
| Определение: |
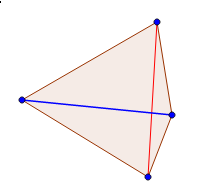
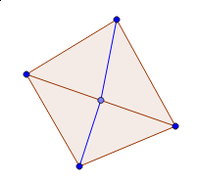
| Рассмотрим пару смежных треугольников. Рёбра этих треугольников образуют четырёхугольник с проведённой в нём диагональю. Операция замены этой диагонали на другую называется flip (флип). |
Из леммы 3 следует, что если ребро плохое, то флип сделает его хорошим.
| Лемма (5): |
Флип плохого ребра уменьшает разность объёмов параболоида и триангуляции, спроецированной на него. |
| Доказательство: |
|
Рассмотрим два таких смежных треугольника, что ребро между ними является плохим. Спроецируем их на параболоид. Четыре точки, принадлежащие смежным треугольникам, при проекции на параболоид образуют тетраэдр. Проведём через какой-нибудь из двух треугольников плоскость. Вершина, противолежащая основанию тетраэдра, являющегося этим треугольником, лежит ниже этой плоскости (так как не выполняется локальный критерий Делоне), то есть тетраэдр лежит ниже тела, образующегося при проекции всей триангуляции на параболоид. После флипа станет выполняться локальный критерий Делоне, то есть тело станет включать в себя тетраэдр. Поэтому после флипа плохого ребра объём тела увеличится на объём этого тетраэдра. |
| Лемма (6): |
Флипами можно достичь хорошей триангуляции за конечное время. |
| Доказательство: |
| Всего триангуляций заданного множества точек конечное число, и среди них есть триангуляция Делоне. Последовательность флипов плохих рёбер триангуляции образует такую последовательность триангуляций, что разность объёмов параболоида и спроецированной на него триангуляции убывает (по лемме 5). Эта последовательность конечна (при этом последней в последовательности является триангуляция Делоне), значит, число флипов, требуемых для достижения триангуляции Делоне, тоже конечно. |
| Лемма (7): |
Если в триангуляцию Делоне вставить точку в некоторый треугольник и соединить его вершины с этой точкой, то получившиеся рёбра будут хорошими. |
| Доказательство: |
|
Предположим, точка была вставлена не на ребро. Рассмотрим любое из рёбер — пусть это будет ребро . Проведём окружность, описывающую треугольник . По критерию Делоне в ней не будет никаких точек триангуляции. На ребре можно построить окружность, изнутри касающуюся окружности, описанной вокруг треугольника. В ней тоже нет никаких точек. Значит, для выполняется критерий Делоне для рёбер, то есть, оно хорошее. Случай, когда точка вставляется на ребро, рассматривается аналогично. |
Вставка точки
Вставка точки, лежащей внутри триангуляции
Для начала локализуемся: поймём, в каком фейсе лежит точка (или на каком ребре).
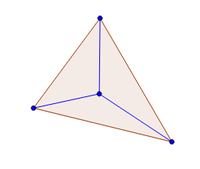
Если точка лежит внутри фейса, добавляем три ребра, сам фейс превращаем в один из новых смежных с вставляемой точкой и добавялем ещё два фейса.
Если же точка лежит на ребре, два смежных с ребром фейса превращаем в два новых, добавляем ещё два, а так же превращаем ребро, на которое вставляется точка, в ребро, которое заканчивается в этой точке, и вставляем три новых.
Итого у нас появилось несколько новых рёбер. Они все хорошие (по лемме 7), плохими могут оказаться только рёбра, противолежащие вставленной точке. Флипаем рёбра, пока триангуляция не станет хорошей.
Вставка точки, лежащей снаружи триангуляции
Представим, что вне триангуляции — бесконечные треугольники, основания которых — рёбра выпуклой оболочки триангуляции, а противолежащая ребру вершина — это бесконечно удалённая точка. Тогда понятно, что вставка точки, не лежащей в триангуляции, сведётся к вставке точки внутрь триангуляции, если мы научимся обрабатывать бесконечные фейсы.
Бесконечно удалённая точка имеет координаты (последняя координата — однородная).
Тогда проверка на то, является ли хорошим ребро, инцидентное бесконечно удалённой точке, упрощается: , то есть достаточно проверить поворот трёх остальных точек образованного двумя бесконечными треугольниками четырёхугольника.
Проверка, принадлежит ли точка бесконечному треугольнику, тоже проста: нужно, чтобы из точки было видно ребро, противолежащее бесконечно удалённой точке, в бесконечном треугольнике. Это проверяется предикатом поворота.
Время работы
| Лемма (8): |
При вставке точки будут флипаться только рёбра, противолежащие вставленной точке. |
| Доказательство: |
|
Доказательство по индукции. База. По лемме 7 изначально не будут флипаться новые рёбра, инцидентные точке, то есть плохими могут оказаться только рёбра, противолежащие точке. Переход. Рассмотрим, что произойдёт с противолежащим точке ребром после флипа, если оно плохое. До вставки точки для триангуляции выполнялся глобальный критерий Делоне, поэтому в окружности, описанной вокруг треугольника , не будет лежать никаких точек, кроме точки . Можно построить окружность, касающуюся её изнутри в точке и проходящую через точку . В ней тоже не окажется никаких точек, так как она касается изнутри. Значит, для ребра выполняется критерий Делоне. Значит, после флипа ребро уже не будет флипаться. Так как для рёбер и выполняется критерий Делоне, то плохими после флипа могут стать только рёбра и — то есть рёбра, противолежащие точке . |
| Лемма (9): |
Средняя степень вершины после вставки её в триангуляцию Делоне равна . |
| Доказательство: |
|
Предположим, что мы вставляем -ую точку из последовательности из точек. Рассмотрим все перестановки из этих точек, означающие порядок вставки этих точек. Всего таких перестановок . Тогда средняя степень последней вершины среди перестановок равна:
Каждая из вершин побывает последней ровно раз, поэтому: |
| Теорема: |
При вставке точки в триангуляцию Делоне в среднем придётся сделать флипов. |
| Доказательство: |
| Все флипнутые рёбра окажутся инцидентными вставленной точке (по лемме 8), а степень вершины — (по лемме 9). Поэтому будет сделано флипов. |
Так как среднее число флипов — , то время вставки целиком зависит от времени локализации.
Удаление точки
Алгоритм
При удалении точки получится звёздный многоугольник, который можно затриангулировать за линию. При этом все рёбра, полученные в результате триангуляции звёздного многоугольника, могут оказаться плохими, поэтому необходимо пройтись по ним и пофлипать, если нужно.
Время работы
Средняя степень вершины в триангуляции — , поэтому триангуляция звёздного многоугольника будет тоже за . Новых рёбер получится , проверить их на локальный критерий Делоне и пофлипать тоже можно за . Итого удаление точки работает за .
Локализационная структура
Cтруктура
Локализационная структура состоит из нескольких уровней, где каждый уровень — это триангуляция Делоне. На нижнем уровне содержатся все точки. Каждая точка с вероятностью проходит на следующий уровень (причём если точка — единственная на последнем уровне, то дальше она не пройдёт).
Уровни связаны между собой следующим образом: на уровне каждая точка содержит указатель на себя же на уровне .
Алгоритм локализации
Как происходит локализация: нам дают точку , которая на предыдущем уровне была ближайшей к точке , которую мы локализуем. Нужно получить следующую точку , которая будет ближайшей уже на этом уровне. Делается это следующим образом:
- Находим, в каком из треугольников, смежных с , лежит отрезок
- Находим, какие рёбра треугольников пересекает , в итоге находим треугольник, в котором лежит
- Находим ближайшую к точку. Первым кандидатом на то, чтобы быть ближайшей точкой, становится ближайшая к вершина найденного в предыдущем пункте треугольника. Для каждого кандидата нужно просмотреть смежные вершины в поиске точки, которая находится ближе к — эта точка становится следующим кандидатом. Если же среди соседей точки не нашлось более близких, значит, эта точка и есть ближайшая.
Корректность алгоритма
| Теорема: |
Данный алгоритм найдёт ближайшую точку. |
| Доказательство: |
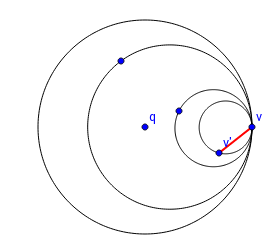
| Предположим, что это не так. Назовём локализуемую точку , а последнего кандидата на то, чтобы быть ближайшей точкой — . Раз эта точка на самом деле не ближайшая, то в окружности, проходящей через , с центром в точке найдутся ещё какие-то точки, не смежные с . Проведём через каждую из них окружность, касающуюся изнутри в точке изначальную окружность. Рассмотрим точку , через которую проходит наименьшая окружность из построенных. В этой окружности не будет лежать никаких точек, так как мы взяли наименьшую. Значит, ребро удовлетворяет критерию Делоне и должно являться ребром триангуляции (по лемме 2), но по предположению этого ребра нет. Значит, предположение неверно. |
Время работы, требуемая память
Память
| Лемма (10): |
Матожидание числа уровней в локализационной структуре — . |
| Доказательство: |
|
Для оценки матожидания посчитаем вероятность того, что количество уровней равно при вероятности пройти на следующий уровень равной . , потому что вероятность того, что точка дойдёт до уровня , равна . , потому что вероятность того, что точка не дойдёт до уровня , равна .
Оценим первую сумму: , поскольку сумма этих вероятностей не превосходит единицу. Оценим вторую сумму:
Рассмотрим эту сумму: Суммируя всё вышесказанное, получаем, что . |
| Теорема: |
Локализационная структура занимает памяти. |
| Доказательство: |
| Триангуляция для точек занимает памяти. На нулевом уровне точек. На уровне точек . Получим геометрическую прогрессию, сумма которой равна . |
Время работы
| Лемма (11): |
Каждая точка на плоскости может являться ближайшей для не более чем шести точек. |
| Доказательство: |
|
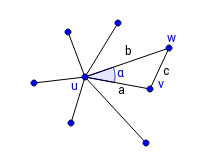
Предположим, что это не так. Пусть некоторая точка является ближайшей для семи точек. Соединим эти семь точек с точкой отрезками и рассмотрим минимальный из углов, который образуют проведённые отрезки и . Этот угол меньше 60° (иначе все семь углов больше либо равны 60° и их сумма больше 360°). Так как точка ближайшая для точек и , то — наибольшая сторона в треугольнике . В треугольнике наибольшая сторона лежит напротив наибольшего угла. Но напротив стороны лежит угол меньше 60°, значит, сумма углов треугольника меньше 180°. Противоречие. Значит, предположение неверно. |
| Лемма (12): |
Для заданной точки на -ом уровне средняя степень ближайшей на -ом уровне вершины равна . |
| Доказательство: |
|
Функция принимает точку и множество и возвращает ближайшего соседа заданной точки из заданного множества. Рассмотрим некоторый уровень . Определим множество . Рассмотрим все возможные подмножества , равномощные , тем самым рассмотрев все возможные уровни . Для каждой точки из каждого подмножества рассмотрим степень ближайшей вершины и усредним всё, получив нужную нам оценку.
Назовём графом двудольный граф, в левой и правой долях содержащий точки , рёбра которого означают, что точка является ближайшей для точки (точка лежит в левой доли, точка лежит в правой доли). Понятно, что , так как степень каждой вершины учтётся ровно столько раз, сколько рёбер ей инцидентно в правой доли графа .
По лемме 11 степень вершины из правой доли графа не может быть больше шести. |
| Лемма (13): |
Среднее число точек, лежащих в окружности с центром в точке и проходящей через , равно . |
| Доказательство: |
|
Рассмотрим точки триангуляции . Для каждой точки построим окружность с центром в точке , проходящую через ближайшую к ней точку. Докажем, что заданная точка попадёт в таких окружностей на предыдущем уровне. Разделим плоскость на шесть частей прямыми, проходящими через точку . Рассмотрим одну из частей. Отсортируем все точки, попавшие в неё, по увеличению расстояния до . Получим такую последовательность точек , что . Заметим, что если какая-нибудь точка содержится на предыдущем уровне, то все точки, начиная с уже не содержат в своей окружности точку . Таким образом, среднее число точек , в окружности которых содержится точка : Таким образом, каждая точка содержится в окружностей, значит, каждая окружность содержит точек. |
| Лемма (14): |
Среднее число рёбер, пересечённое отрезком во втором этапе алгоритма локализации, равно . |
| Доказательство: |
|
Рассмотрим рёбра, пересекающие , для которых хотя бы одна из граничных точек окажется в окружности с центром в точке , проходящей через . Число таких рёбер не превосходит суммы степеней вершин, лежащих внутри окружности. А по лемме 13 число таких точек равно . При этом средняя степень вершины равна . Таким образом, число таких рёбер равно . Докажем, что число рёбер, пересекающих , для которых обе граничные точки лежат вне окружности, тоже равно . При вставке точки в триангуляцию для этих рёбер перестанет выполняться критерий Делоне: в любой окружности, построенной на ребре как на хорде, будет содержаться либо точка , либо точка . Поэтому эти рёбра придётся флипнуть. Число флипов при вставке точки равно , поэтому число таких рёбер равно . Итого число рёбер, пересекающих , равно . |
| Лемма (15): |
Среднее число треугольников, посещённых на третьем этапе алгоритма локализации, равно . |
| Доказательство: |
| Каждый рассмотренный треугольник имеет хотя бы одну вершину внутри окружности, проведённой через , с центром в точке . То есть число таких треугольников не больше числа точек внутри этой окружности. Таких точек по лемме 13 , значит, число треугольников тоже равно . |
| Лемма (16): |
Локализация точки на каждом уровне происходит за . |
| Доказательство: |
|
Докажем, что каждый этап локализации происходит за . 1 этап: по лемме 12 средняя степень вершины равна , поэтому треугольников, в которых может лежать отрезок тоже . Просмотрев их все, за можно понять, в каком из них лежит отрезок . 2 этап: число рёбер, пересечённых отрезком , равно (по лемме 14). Поэтому этот этап локализации тоже происходит за . 3 этап: число треугольников, посещённых на третьем этапе локализации, равно (по лемме 15). |
| Теорема: |
Локализация точки в триангуляции происходит за . |
| Доказательство: |
| Очевидное следствие из леммы 10 и леммы 16. |
Constraints
| Определение: |
| Констрейнты — рёбра, которые нельзя флипать. |
| Утверждение: |
Хорошая триангуляция с констрейнтом может быть хорошей с точностью до видимости через констрейнт. |
Вставка
Смотрим на список рёбер, пересечённых ещё не вставленным констрейнтом, и флипаем их. Последнее флипнутое ребро и будет констрейнтом (по понятным причинам), после флипа пометим его как констрейнт. Затем флипаем всё, что могло стать плохим (кроме констрейнта), пока триангуляция вновь не станет хорошей.
Удаление
Аналогично: помечаем ребро как не-констрейнт и флипаем, пока не дойдём до хорошей триангуляции.