Уменьшение размерности
Под уменьшением размерности (англ. dimensionality reduction) в машинном обучении подразумевается уменьшение числа признаков набора данных. Наличие в нем признаков избыточных, неинформативных или слабо информативных может понизить эффективность модели, а после такого преобразования она упрощается, и соответственно уменьшается размер набора данных в памяти и ускоряется работа алгоритмов ML на нем. Уменьшение размерности может быть осуществлено методами выбора признаков (англ. feature selection) или выделения признаков (англ. feature extraction).
Содержание
Выбор признаков
Методы выбора признаков оставляют некоторое подмножество исходного набора признаков, избавляясь от признаков избыточных и слабо информативных. Основные преимущества этого класса алгоритмов:
- Уменьшение вероятности переобучения;
- Увеличение точности предсказания модели;
- Сокращение времени обучения;
- Увеличивается семантическое понимание модели.
Все методы выбора признаков можно разделить на 5 типов, которые отличаются алгоритмами выбора лишних признаков.
Фильтры
Фильтры (англ. filter methods) измеряют релевантность признаков на основе функции $\mu$, и затем решают по правилу $\kappa$, какие признаки оставить в результирующем множестве.
Фильтры могут быть:
- Одномерные (англ. univariate) — функция $\mu$ определяет релевантность одного признака по отношению к выходным меткам. В таком случае обычно измеряют "качество" каждого признака и удаляют худшие;
- Многомерные (англ. multivariate) — функция $\mu$ определяет релевантность некоторого подмножества исходного множества признаков относительно выходных меток.
Распространенными вариантами для $\mu$ являются:
- Коэффициент ранговой корреляции Спирмена [1](англ. Spearman's rank correlation coefficient): $p(x, y)=\displaystyle \frac{\sum_{i, j}(x_{ij}-\bar{x_j})(y_i-\bar{y})}{\sqrt{\sum_{i, j}(x_{ij}-\bar{x_j})^2\sum_i(y_i-\bar{y})^2}}$;
- Information gain[2]: $IG(x, y)=\displaystyle -\sum_{i=1}^kp(c_i)\log_2{(p(c_i))}+\sum_{i=1}^{n}p(t_i)\sum_{j=1}^kp(c_j|t_i)log_2{(p(c_j|t_i))}$, и другие.
Преимуществом группы фильтров является простота вычисления релевантности признаков в наборе данных, но недостатком в таком подходе является игнорирование возможных зависимостей между признаками.
Оберточные методы
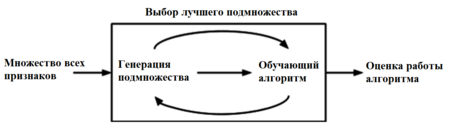
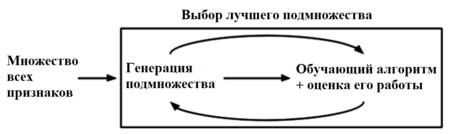
Оберточные методы (англ. wrapper methods) находят подмножество искомых признаков последовательно, используя некоторый классификатор как источник оценки качества выбранных признаков, т.е. этот процесс является циклическим и продолжается до тех пор, пока не будут достигнуты заданные условия останова. Оберточные методы учитывают зависимости между признаками, что является преимуществом по сравнению с фильтрами, к тому же показывают большую точность, но вычисления занимают длительное время, и повышается риск переобучения.
Существует несколько типов оберточных методов: детерминированные, которые изменяют множество признаков по определенному правилу, а также рандомизированные, которые используют генетические алгоритмы для выбора искомого подмножества признаков. Среди детерминированных алгоритмов самыми простыми являются:
- SFS (Sequential Forward Selection) — жадный алгоритм, который начинает с пустого множества признаков, на каждом шаге добавляя лучший из еще не выбранных признаков в результирующее множество;
- SBS (Sequential Backward Selection) — алгоритм обратный SFS, который начинает с изначального множества признаков, и удаляет по одному или несколько худших признаков на каждом шаге.
Популярным оберточным методом является SVM-RFE (SVM-based Recursive Feature Elimination), который иногда также обозначается как встроенный [3]. Этот метод использует как классификатор SVM[на 28.01.19 не создан] и работает итеративно: начиная с полного множества признаков обучает классификатор, ранжирует признаки по весам, которые им присвоил классификатор, убирает какое-то число признаков и повторяет процесс с оставшегося подмножества фичей, если не было достигнуто их требуемое количество. Таким образом, этот метод очень похож на встроенный, потому что непосредственно использует знание того, как устроен классификатор.
Встроенные методы
Группа встроенных методов (англ. embedded methods) очень похожа на оберточные методы, но для выбора признаков используется непосредственно структуру некоторого классификатора. В оберточных методах классификатор служит только для оценки работы на данном множестве признаков, тогда как встроенные методы используют какую-то информацию о признаках, которую классификаторы присваивают во время обучения.
Одним из примеров встроенного метода является реализация на случайном лесе: каждому дереву на вход подаются случайное подмножество данных из датасета с каким-то случайным набор признаков, в процессе обучения каждое из деревьев решений производит "голосование" за релевантность его признаков, эти данные агрегируются, и на выходе получаются значения важности каждого признака набора данных. Дальнейший выбор нужных нам признаков уже зависит от выбранного критерия отбора.
Встроенные методы используют преимущества оберточных методов и являются более эффективными, при этом на отбор тратится меньше времени, уменьшается риск переобучения, но т.к. полученный набор признаков был отобран на основе знаний о классификаторе, то есть вероятность, что для другого классификатора это множество признаков уже не будет настолько же релевантным.
Другие методы
Есть и другие методы выбора признаков: гибридные (англ. hybrid methods) и ансамблевые (англ. ensemble methods). Гибридные методы комбинируют несколько разных методов выбора признаков, например, некоторое множество фильтров, а потом запускают оберточный или встроенный метод. Таким образом, гибридные методы сочетают в себе преимущества сразу нескольких методов, и на практике повышают эффективность выбора признаков.
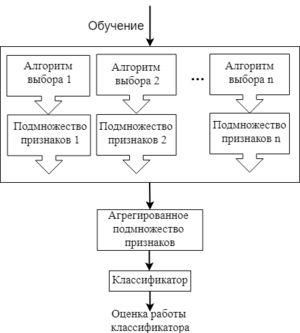
Ансамблевые методы применяются больше для наборов данных с очень большим числом признаков. В данном подходе для начального множества признаков создается несколько подмножеств признаков, и эти группы каким-то образом объединяются, чтобы получить набор самых релевантных признаков. Это довольно гибкая группа методов, т.к. для нее можно применять различные способы выбора признаков и объединения их подмножеств.
Примеры кода scikit-learn
Пример кода, реализующего функцию оценки фильтра на основе коэффициента ранговой корреляции:
# Импорт библиотек
import pandas as pd
import numpy as np
# Вспомогательная функция для расчета корреляции
def correlation(X, Y):
return np.cov(X, Y) / np.sqrt(np.var(X) * np.var(Y))
# Сам фильтр на основе метрики ранговой корреляции
# Аргументы X -- значения объектов датасета для какой-то фичи, Y -- метки этих объектов
def measure_spearmans(X, Y):
xr = pd.Series(X).rank()
yr = pd.Series(Y).rank()
return correlation(xr, yr)
Пример кода, реализующего SVM-RFE wrapper:
# Импорт библиотек import numpy as np import pandas as pd from sklearn import svm
# X -- наш датасет, Y -- массив меток
# N -- число признаков, которые хотим оставить, step -- сколько фичей удаляется на каждой итерации
# Возвращает массив из булевых переменных размерностью 1x[число признаков], показывающий, отбрасываем признак или нет
def RFE(X, Y, N, step = 10):
# cache_size нужен, если набор данных большой, иначе можно опустить
clfRFE = svm.SVC(kernel='linear', cache_size=1024)
featureCount = X.shape[1]
featureList = np.arange(0, featureCount )
included = np.full(featureCount, True)
curCount = featureCount
while curCount > N:
actualFeatures = featureList[included]
Xnew = X[:, actualFeatures]
clfRFE.fit(Xnew, Y)
curStep = min(step, curCount - N)
elim = np.argsort(np.abs(clfRFE.coef_[0]))[:curStep]
included[actualFeatures[elim]] = False
curCount -= curStep
return included
Выделение признаков
Другим способом уменьшить размерность входных данных является выделение признаков. Эти методы каким-то образом составляют из уже исходных признаков новые, все также полностью описывающие пространство набора данных, но уменьшая его размерность и теряя в репрезентативности данных, т.к. становится непонятно, за что отвечают новые признаки. Все методы feature extraction можно разделить на линейные и нелинейные.
Одним из самых известных методов линейного выделения признаков является PCA[на 28.01.19 не создан] (Principal Component Analysis, рус. метод главных компонент). Основной идеей этого метода является поиск такой гиперплоскости, на которую при ортогональной проекции всех признаков максимизируется дисперсия. Данное преобразование может быть произведено с помощью сингулярного разложения матриц и создает проекцию только на линейные многомерные плоскости, поэтому и метод находится в категории линейных.
К нелинейным методам, например, могут быть отнесены методы отображающие исходное пространство признаков на нелинейные поверхности или топологические многообразия. Одним из таких алгоритмов является t-SNE[на 28.01.19 не создан] (t-distributed Stochastic Neighbor Embedding, рус. стохастическое вложение соседей с t-распределением). Данный метод состоит из двух шагов: изначально строится распределение вероятностей по всем парам точек набора данных, каждая условная вероятность $p_{j|i}$ которого означает насколько точка $X_j$ близка к точке $X_i$ при гауссовом распределении вокруг $X_i$. Данное распределение как метрику похожести использует евклидово расстояние. Алгоритм старается получить отображение из точек размерности $\mathbb{R}^k$ в меньшую размерность $\mathbb{R}^d$, для этого вводится еще одно распределение, описывающее насколько точки из нового пространства похожи друг на друга, но используя при этом t-распределение Стьюдента с одной степенью свободы. Как метрику похожести двух распределений используется дивергенция Кульбака-Лейблера[4], и чтобы найти точки новой размерности $d$ запускается градиентный спуск для минимизации этой величины.
Пример кода scikit-learn
Пример выделения признаков с помощью PCA в scikit-learn:
# Импорт библиотек from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split
X = ... # загрузка X Y = ... # загрузка Y # Разделение данных на train и test Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, Y)
clf = ... # берем какой-то классификатор
# Обучаем PCA для выделения 5 признаков
pca = PCA(n_components=5)
pca.fit(Xtrain)
# Изменяем наши наборы данных под выбранные признаки
Xtrain = pca.transform(Xtrain)
Xtest = pca.transform(Xtest)
# Обучаем классификатор и проверяем точность его работы
clf.fit(Xtrain, Ytrain)
print ("Score: %.6f" % clf.score(Xtest, Ytest))
Пример на языке Scala
SBT зависимость:
libraryDependencies += "com.github.haifengl" %% "smile-scala" % "1.5.2"
Пример уменьшение размерности используя smile.feature.GAFeatureSelection[5]:
import smile.classification._ import smile.data._ import smile.feature.GAFeatureSelection import smile.read import smile.validation.Accuracy
// Загрузка данных val data = read.arff("data/weka/segment-test.arff", 19) val (x, y) = data.unzipInt val trainer = new GradientTreeBoost.Trainer(100) val measure = new Accuracy // Cоздание генетического алгоритма и его настройка. val selector = new GAFeatureSelection // Размер популяции - 50, количество поколений - 20 // Каждая возращаемая BitString содержит фичи и их качество. val result = selector.learn(50, 20, trainer, measure, x, y, 5) result.foreach { bits => print(100*bits.fitness) println(bits.bits.mkString(" ")) }
Пример на языке Java
Пример уменьшения размерности датасета с применением weka.attributeSelection.PrincipalComponents[6]
Maven зависимость:
<dependency> <groupId>nz.ac.waikato.cms.weka</groupId> <artifactId>weka-stable</artifactId> <version>3.8.0</version> </dependency>
import weka.attributeSelection.PrincipalComponents; import weka.core.Instances; import weka.filters.Filter; import weka.filters.unsupervised.attribute.NumericToNominal; import java.io.BufferedReader; import java.io.FileReader;
// load dataset
var data = new Instances(new BufferedReader(new FileReader("data/bank-data.arff")));
var filter = new NumericToNominal();
filter.setInputFormat(data);
data = Filter.useFilter(data, filter);
// initialize the PCA-based selector
var pca = new PrincipalComponents();
// dimensionality reduction is achieved through selecting enough eigenvectors to account
// for some percantege of the variance in the original data
pca.setVarianceCovered(0.95);
pca.buildEvaluator(data);
// transform the dataset
data = pca.transformedData(data);
См. также
- Переобучение
- SVM[на 28.01.19 не создан]
- Случайный лес
- PCA[на 28.01.19 не создан]
- t-SNE[на 28.01.19 не создан]
Примечания
Источники информации
- Sequential feature selection — курс ML Texas A&M University
- Feature selection — статья про Feature Selection в Wikipedia
- Публикация про feature selection
- Embedded random forest