Упрощение полигональной цепи
Упрощение полигональной цепи — процесс, позволяющий уменьшить число точек полилинии.
Содержание
Задача
Дана некоторая полилиния, заданная последовательностью точек , и некоторое . Требуется найти цепь , являющейся подпоследовательностью исходной. Для этой цепи верно, что для всех , таких что для любых соседних и .
Существует также альтернативная задача, в которой вместо задано число вершин в итоговой цепи. В этом случае требуется составить цепь заданной длины таким образом, что максимально необходимое для условия было минимально.
Также упрощение можно выполнять с помощью введения новой полилинии, не сохраняющей точки исходной, но такая вариация задачи рассмотрена не будет.
Мотивация
Такая задача встречается при обработки векторной графики и построении карт. Например, есть цепь, несколько точек которой попадают в один и тот же пиксель. Очевидно, что тогда можно упростить все эти точки в одну. В этом случае и пригодится упрощение, одним из вариантов реализации которого является алгоритм Дугласа-Пекера (Douglas-Peucker).
В случае, когда у нас есть несколько устройств с разным dpi, например, монитор и принтер, то, взяв за половину расстояния, которое помещается на одной из границ пикселя, мы можем растеризовать одну и ту же цепь для разных устройств.
Алгоритм Дугласа-Пекера
Алгоритму задается исходная полилиния и максимальное расстояние, которое может быть между исходной и упрощённой полилиниями (то есть, максимальное расстояние от точек исходной к ближайшему участку полученной полилинии). Упрощенная полилиния состоит из подмножества точек, которые определяются из исходной.
Описание
Начальная полилиния представляет собой упорядоченный набор точек.
Алгоритм рекурсивно делит полилинию. Входом алгоритма служат координаты всех точек между первой и последней включая их, а так же . Первая и последняя точка сохраняются неизменными. После чего алгоритм находит точку, наиболее удалённую от отрезка, состоящего из первой и последней (оптимальный способ поиска расстояния от точки до отрезка рассмотрен ниже). Если точка находится на расстоянии, меньше, чем , то все точки, которые ещё не были отмечены к сохранению, могут быть выброшены из набора, и получившаяся прямая сглаживает кривую с точностью не ниже .
Если же расстояние больше , то алгоритм рекурсивно вызывает себя на наборе от начальной до данной и от данной до конечной точек (данная точка будет отмечена к сохранению).
По окончанию всех рекурсивных вызовов итоговая полилиния строится только из тех точек, что были отмечены к сохранению.
Псевдокод
DouglasPeucker(int first, int last, double eps)
max = -infinityindex = -1for (int i = first + 1; i < last; i++)distance = dist(points[i], segment(points[first],points[last]))if (distance > max && distance > eps)max = distance, index = i
if(index == -1)return
elseanswer[index] = trueDouglasPeucker(first, index, eps)DouglasPeucker(index, last, eps)
Пример
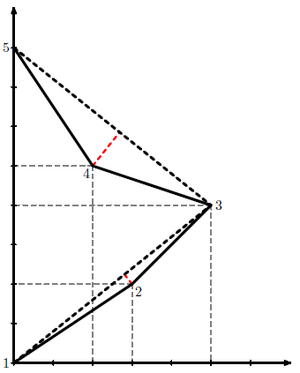
Рассмотрим пример для точек, заданных на рисунке, где сплошная линия отражает исходную линию, и .
| Шаг | Действие |
|---|---|
| Найдем наиболее удаленную точку от отрезка , это точка | |
| Расстояние до точки больше , добавляем ее в ответ | |
| Запустим алгоритм для точек и | |
| Найдем наиболее удаленную точку от отрезка , это точка | |
| Расстояние до точки меньше , возвращаемся | |
| Запустим алгоритм для точек и | |
| Найдем наиболее удаленную точку от отрезка , это точка | |
| Расстояние до точки меньше , возвращаемся | |
| Алгоритм завершен |
Полилиния, полученная в результате работы алгоритма, отражается черной пунктирной линией.
Время работы
Ожидаемая сложность алгоритма может быть оценена выражением в лучшем случае, когда номер наиболее удаленной точки всегда оказывается лексикографически центральным. Однако, в худшем случае сложность алгоритма составляет . Это достигается, например, в случае, если номер наиболее удаленной точки всегда соседний к номеру граничной точки.
Замечания к алгоритму
Топология
К сожалению, алгоритм Дугласа-Пекера в ходе своей работы не сохраняет топологию. Это означает, что в ответе мы можем получить линию с самопересечениями.
В статье де Берга (de Berg) "A New Approach to Subdivision Simplification"(1995) приведен алгоритм, позволяющий решать чуть более общую задачу, чем текущая: упрощение полигональной цепи с учетом обязательных особых точек, не входящих в нее и с учетом топологии. Можно использовать алгоритм и для текущего случая, задав множество особых точек пустым. Время работы алгоритма при этом составит . Краткое описание алгоритма дано ниже.
Оптимальность
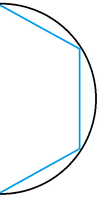
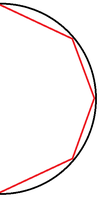
Алгоритм может находить не минимальный по количеству точек ответ. Рассмотрим пример, в котором исходная линия с некоторым приближением будет представлять полуокружность. Мы можем подобрать такое , что алгоритм добавит три точки помимо стартовой и конечной (точки через каждую четверть исходной линии), в то же время мы можем взять две точки через каждую треть исходной линии, для которых упрощение также верно.
Решение альтернативной задачи
Решение альтернативной задачи очень схоже с исходном алгоритмом. На каждой итерации алгоритм находит подучасток исходной цепи, на котором расстояние до наиболее удаленной точки максимально, делит ее так же как и в исходном алгоритме и запоминает полученные в результате деления подучастки для следующих итераций. Алгоритм стартует, когда для выбора доступна только исходная цепь.
Реализация
Практически очевидно, что данный вариант алгоритма легко реализовать на приоритетной очереди. Будем хранить расстояние, на котором находится наиболее удаленная вершина, как ключ, а номера вершин-границ как значение. На каждой итерации мы выбираем обьект с наибольшим ключем, делим и получившиеся части кладем обратно в очередь с новыми ключами.
Поиск расстояния от точки до отрезка
Идея
При определении расстояния от точки до отрезка нужно сначала проанализировать взаимное расположение точки и отрезка прямой, то есть, проверить, куда опустится перпендикуляр из точки: непосредственно на отрезок или на прямую, являющуюся продолжением рассматриваемого отрезка.
Если перпендикуляр падает на отрезок, то ответом будет расстояние от исходной точки до точки пересечения отрезка с перпендикуляром, иначе — расстояние от исходной точки до одного из концов отрезка.
Самое очевидное — найти точку пересечения перпендикуляра и прямой и, в зависимости от ее положения, вычислить ответ. Или же, этот анализ может быть произведен путем построения треугольника, вершинами которого являются концы отрезка и точка, и сопоставления соотношения длин его сторон.
Реализация
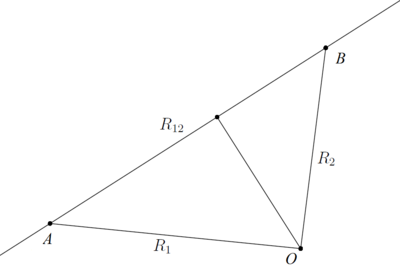
Даны точка и отрезок, заданный точками и .
Введём обозначения:
- — отрезок
- — отрезок
- — отрезок
Если:
- , то ответ это , так как угол между и при данном условии
- , то ответ это , так как угол между и при данном условии
- Оба предыдущих условия ложны, то , где и . Это следует из формул для площади параллелограмма через векторное произведение и через произведения основания на высоту
Обзор ускорения работы алгоритма Дугласа-Пекера
Как описано выше, в худшем случае алгоритм работает за . Можно внести дополнения, которые позволят получить в худшем случае. Ускорение основывается на уменьшении времени поиска наиболее удаленной вершины. Это можно осуществить благодаря идее о том, что наиболее удаленная вершина лежит на выпуклой оболочке полигональной цепи. Описание ускорения взято из статьи Хершберга(Hershberger) "Speeding Up the Douglas-Peucker Line-Simplification Algorithm" (1992).
Для построения выпуклой оболочки используется алгоритм Мелкмана, который работает для двумерной полигональной цепи без самопересечений за , строя все промежуточные выпуклые оболочки, которые пригодятся в дальнейшем.
После построения выпуклой оболочки используется бинарный поиск для нахождения наиболее удаленной вершины за . Затем, если потребуется, действия повторятся рекурсивно, как и в оригинальном алгоритме, но заново строить оболочки не имеет смысла, так как промежуточные уже были построены. Использовав их, можно разбить текущую оболочку на две за .
В итоге получается, что в худшем случае разбиений за и поиск за , что дает .
Замечания
К сожалению, у данного метода есть несколько недостатков по сравнению с оригинальным алгоритмом, некоторые из которых уже были упомянуты:
- исходная цепь должна быть без самопересечений для использования алгоритма Мелкмана
- ускорение подходит лишь для двумерного случая из-за способа построения выпуклой оболочки
- в некоторых случаях оригинальный алгоритм Дугласа-Пекера работает быстрее (например в случае, когда цепь приближено является окружностью)
Алгоритм Реуманна-Виткама
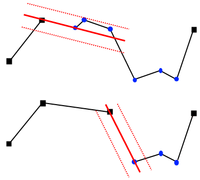
Алгоритм Реуманна-Виткама (Reumann-Witkam) определяет прямую через первые две точки цепи, последняя из последовательных точек начиная со второй, удаленных небольше чем на , соединяются прямой, а все промежуточные точки исключаются.
Алгоритм продолжится последовательно для оставшихся точек до тех пор, пока не будет достигнута последняя.
На рисунке прямая, проходящая через точки отображена красной линией, границы, в которые попадают вершины, допустимые для упрощения, отображены красными пунктирными линиями, точки попавшие в итоговую цепь отображены черным.
Алгоритм Опхейма
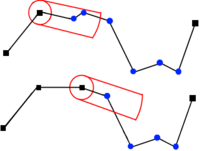
Алгоритм Опхейма (Opheim) несколько схож с алгоритмом Реуманна-Виткама. В этом алгоритме мы рассматриваем все вершины в радиусе от первой, и строим луч из текущей и последней, попавшей в радиус. Если таких точек нет, то берется следующая за исходной.
Последующие вершины упрощаются до тех пор, пока их расстояние до луча превосходит и радиальное расстояние до первой точки превосходит . Затем алгоритм продолжается для оставшихся точек до тех пор, пока не будет достигнута последняя.
На рисунке радиус, луч и максимальное радиальное расстояние отображены красными линиями и дугами. Точки попавшие в итоговую цепь отображены черным.
Алгоритм Ланга
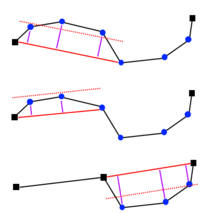
Алгоритм Ланга (Lang) определяет фиксированный размер поисковой области для упрощения. Две точки, что образуют поисковую область, составляют отрезок. Этот отрезок используется для расчета перпендикулярного расстояния до каждой промежуточной точки. Если рассчитанное расстояние больше заданного , область поиска будет уменьшен путем исключения ее последней точки.
Этот процесс будет продолжаться, пока все рассчитанные расстояния не будут ниже заданного , или когда нет больше промежуточных точек. Все промежуточные точки удаляются, а новая область поиска определяется, начиная с последней точки в старой области.
На рисунке граница поисковой области помечена красной линией, допустимая область для упрощения - красной пунктирной линией, точки попавшие в итоговую цепь отображены черным.
Алгоритм, сохраняющий топологию
Алгоритм сохраняющий топологию, как было упомянуто ранее, содержится в статье де Берга A New Approach to Subdivision Simplification, где расскрываются также детали реализации, здесь же описывается идея алгоритма. Также стоит обратить внимание, что исходная полигональная цепь должна быть без самопересечений.
Алгоритм делится на четыре основных этапа:
- Создание графа , в котором помимо исходных ребер, добавлены все возможные сокращенные ребра. Иначе говоря ребра, для который верно, что и для любого , такого что , верно .
- Создание графа , в котором добавлены все возможные ребра, не нарушающие топологию. На этом этапе построение выполняется без учета .
- Создание графа , в котором будет содержаться кратчайшая полигональная цепь без самопересечений по построению и .
- Поиск кратчайшего пути в , как в невзвешенном графе, этот путь и будет являться ответом на задачу.
Ссылки
- Алгоритм Дугласа-Пекера
- Поиск расстояния от точки до отрезка
- Поиск расстояния от точки до прямой
- "Speeding Up the Douglas-Peucker Line-Simplification Algorithm"
- Алгоритм Мелкмана
- Алгоритм Мелкмана
- Двоичный поиск на выпуклой оболочке
- "A New Approach to Subdivision Simplification"
- Алгоритмы и визуализатор упрощения полигональной цепи