Adaptive precision arithmetic
Мотивация
Все вычисления, производимые компьютером в модели с плавающей точкой, имеют погрешность. При большом количестве арифметических действий она возрастает. Во многих случаях результирующая погрешность уже не устраивает, и требуется либо абсолютно точное вычисление, либо меньшая погрешность. Одним из решений данной проблемы является хранение чисел в виде рациональных дробей, в которых числитель и знаменатель представляется в виде длинного целого числа. Но работать с такими числами довольно "дорого" по времени и тяжело в реализации: необходимо писать факторизацию чисел, эффективно сокращать дроби. Для улучшения работы нужны определенные оптимизации. Одной из них и является использование адаптивной арифметики (англ. adaptive precision arithmetic).
Базовые понятия
Представление чисел
Большинство современных процессоров поддерживают числа с плавающей точкой в форме . Значащая часть числа (мантисса) представляет собой -битное двоичное число в форме , где каждое обозначает один бит. Также имеется один бит на знак.
Числа с плавающей точкой, как правило, нормализованы, то есть если число не равно нулю, то первый значимый бит равен единице, а экспонента устанавливается соответственно. Например, в -битной арифметике число 1101 (десятичное 13) будет выглядеть как .
Далее в этой статье фраза "что-либо представимо в битах" будет означать представимость в битах мантиссы, не учитывая знак и экспоненту.
Разложения
| Определение: |
| Два числа и называются неперекрывающимися (англ. nonoverlapping), если номер наименьшего значимого бита числа (нумерация справа налево) больше, чем номер наибольшего значимого бита числа , или наоборот. |
Более формально, и не перекрываются, если существует такое целое число и , что и , или и .
Ноль не пересекается ни с одним другим числом.
Например, числа и не пересекаются, а и — пересекаются.
| Определение: |
| Два числа и называются смежными (англ. adjacent), если они перекрываются, если и перекрываются, или и перекрываются. |
Например, числа и — смежные, а и — нет.
Иногда для использовании точной арифметики может понадобиться больше, чем бит для хранения величин. В связи с этим вводится одно из базовых форм хранения чисел для такой арифметики.
| Определение: |
| Разложением числа называется такое его представление , где каждое выражено -битным числом с плавающей точкой и называется компонентой этого разложения. |
| Определение: |
| Разложение называется неперекрывающимся (несмежным), если все его компоненты взаимно не перекрываются (не являются смежными). |
Как правило, разложения должны быть неперекрывающимися, а их компоненты должны быть упорядочены от большей к меньшей по величине (то есть — большая). Далее будут рассматриваться именно такая их форма.
<wikitex>Стоит отметить, что число может быть представлено несколькими возможными неперекрывающимися разложениями: $1100 + -10.1 = 1001 + 0.1 = 1000 + 1 + 0.1$. </wikitex> Неперекрывающиеся разложения нужны, например, для того, чтобы быстро вычислять знак выражения (смотрим знак большей по размеру компоненты), или для грубой оценки значения всего разложения (берем большую по величине компоненту).
Округление
Все алгоритмы, представленные в этой статье, предполагают, что сложение, вычитание и умножение производятся с точным округлением. Предполагается, что числа представляются в битах.
| Определение: |
Точное округление (англ. exact rounding) — такой вид округления, что:
|
Например, в 4-битной арифметике произведение будет округлено в .
При вычислении результата может возникнуть ситуация, когда значение попадает в точности между двумя соседними -битными значениями. Тогда требуется определить правило поведения в таком случае. Рассмотрим некоторые из них.
| Определение: |
| Округление до ближайшего четного (англ. round-to-even) — правило, при котором округление в вышеописанном случае производится к ближайшему -битному четному значению. |
| Определение: |
| Округление к нулю (англ. round-toward-zero) — правило, при котором округление в вышеописанном случае производится -битному значению, находящемуся между точным значением и нулем, а также ближайшему к точному значению. |
Например, в 4-битной арифметике число будет округлено до по первому правилу, и до по второму.
Стоит отметить, что стандарт IEEE 754 использует округление до ближайшего четного по умолчанию.
Далее в этой статье символами и будут обозначаться -битные сложение, вычитание и умножение с точным округлением соответственно.
Из-за округления данные операции теряют некоторые важные свойства, например, ассоциативность: , но .
При анализе округления часто используют так называемый .
| Определение: |
| ULP (англ. units in the last place) — эффективная величина самого младшего (-ого) бита. |
Например, в -битной арифметике.
Так же полезной нотацией является , которая обозначает ошибку округлении результата выполнения операции . Отметим, что если всегда беззнаковая величина, то может иметь знак. Для базовых операций (сложение, вычитание, умножение) , и точное округление гарантирует, что .
Свойства
Иногда есть возможность найти более точные границы ошибки округления, что будет видно далее из лемм. Первая лемма используется, когда один операнд много меньше другого, а вторая - когда сумма близка к степени двойки. Для лемм 1 - 4 пусть - -битные числа с плавающей точкой. Леммы приводятся без доказательств, их можно найти в статье Джонатана Шевчука "Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates".
| Лемма: |
Пусть .
Ошибка округления не превзойдет . (Аналогично для вычитания). |
Как следствие, верна следующая лемма:
| Лемма: |
Ошибка округления может быть представлена в битах. |
| Лемма: |
Пусть и . Тогда . (Аналогично для вычитания). |
| Лемма: |
Пусть . Тогда . |
Алгоритмы суммирования
Простое суммирование
Важной базовой операцией во всех алгоритмах, основанных на представлении чисел в виде разложений, является сумма двух -битных величин, результатом которой является разложение длины два. Есть два алгоритма для выполнения этой задачи - алгоритмы Деккера и Кнута.
Сумма по Деккеру
| Теорема (Dekker): |
Пусть и есть -битные числа, причем . Тогда следующий алгоритм вернет неперекрывающееся разложение такое, что , где - приближение (аппроксимация) суммы , а представляет собой ошибку округления при вычислении . (Аналогично для вычитания). |
Псевдокод для суммы:
Псевдокод для разности:
Отметим, что величины на выходе этой процедуры вовсе не должны иметь один знак, что будет видно из примеров ниже.
В первом примере и имеют один знак.
Во втором примере и имеют противоположные знаки, и .
<wikitex>Проблема с использованием этой процедуры заключается в требовании . Если это заранее не известно, то необходимо выполнить сравнение перед ее вызовом. В большинстве С компиляторов, возможно, самым быстрым переносимым способом реализовать эту проверку является выражение . На эту проверку уйдет некоторое время, но увеличение времени может быть на удивление большим из-за современных процессоров с суперскалярными и конвейерными архитектурами, в которых вызов условного оператора может сбросить ветку предсказаний. Это объяснение лишь гипотетическое и зависит от машины, но алгоритм $\mathrm {TwoSum}$, что будет описан ниже, избегает этого сравнения посредством трех дополнительных операций, что обычно на практике даже быстрее. Конечно же, $\mathrm {FastTwoSum}$ все же быстрее, если результат сравнения известен априори. </wikitex>
Сумма по Кнуту
| Теорема (Knuth): |
Пусть и есть -битные числа, причем . Тогда следующий алгоритм вернет неперекрывающееся разложение такое, что , где — приближение (аппроксимация) суммы , а представляет собой ошибку округления при вычислении . |
Псевдокод:
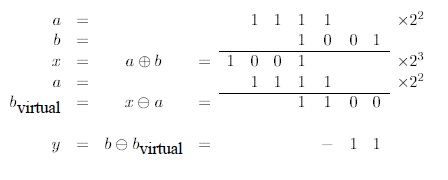
<wikitex>Пример работы последнего алгоритма, когда $|a| < |b|$ и $|a| < |x|$. Сумма $11.11 + 1101$ будет представлена в виде разложение $10000 + 0.11$.
| Лемма: |
Пусть $x$ и $y$ — величины, возращенные алгоритмом $\mathrm {FastTwoSum}$ или $\mathrm {TwoSum}$. На машине с округлением до ближайшего четного $x$ и $y$ — несмежные. |
</wikitex>
Суммирование разложений
<wikitex>Базируясь на алгоритмах сложения двух -битных чисел, описанных выше, можно предложить алгоритмы суммирования разложений. В этой статье их будет предложено два: $\mathrm {ExpansionSum}$ и $\mathrm {FastExpansionSum}$. Первый алгоритм прибавляет к $m$-элементному разложению $n$-элементное разложение за время , в то время, как последний алгоритм делает это за .
Несмотря на такое различие в асимптотике, первый алгоритм на практике может оказаться быстрее на разложениях, чей размер мал и фиксирован, потому что программные циклы могут быть полностью развернуты, а косвенные расходы времени исчезают, так как можно отказаться от использования массива). Линейный же алгоритм имеет определенные условия, при которых подобные оптимизации невозможны.
ExpansionSum имеет свойство, что если входные данные были неперекрывающимися (несмежными), то и на выходе мы получим разложения с соответствующим свойством.
FastExpansionSum имеет несколько серьезных недостатков. Первый из них - алгоритм не сохраняет свойств неперекрываемости/несмежности. Второй - алгоритм основывается на округлении до ближайшего четного, что делает его непереносимым.
Как правило, общим недостатком алгоритмов работы с разложениями является то, что в разложении на выходе могут быть нулевые элементы, даже если в исходном разложении их не было. Например, если подать на вход разложениея $1111 + 0.0101$ и $1100 + 0.11$, то результатом будет $11100 + 0 + 0 + 0.0001$. К счастью, алгоритмы, описанные в этой статье хорошо справляются с этой проблемой. </wikitex>
Перед описанием алгоритмов суммирования разложений, приведем алгоритм прибавления к разложению -битного числа.
Сумма разложения и числа
<wikitex>| Теорема: |
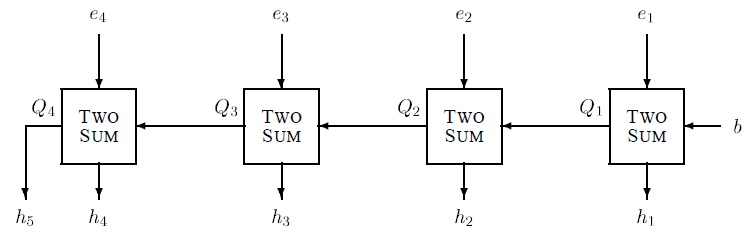
Пусть $e = \sum^{m}_{i=1}e_i$ - неперекрывающееся $m$-компонентное разложение; $b$ - $p$-битное число, где $p \geqslant 3$. Предполагается, что $e_1, e_2, \dots, e_m$ отсортированы в возрастающем порядке, причем все компоненты ненулевые. Тогда следующий алгоритм вернет такое разложение $h$, что $h = \sum^{m + 1}_{i=1}h_i = e + b$, где компоненты $h$ также отсортированы в возрастающем порядке и не равны нулю. Алгоритм также сохраняет свойство несмежности / неперекрываемости. |
Псевдокод для суммы:
$GrowExpansion(e, b)$
$1$ $Q_0 \Leftarrow b$
$2$ $for$ $i = 1 \dots m$
$3$ $(Q_i, h_i) \Leftarrow TwoSum(Q_{i-1}, e_i)$
$4$ $h_{m+1} \Leftarrow Q_m$
$5$ $return$ $h$
$Q_i$ - приближенное значение суммы $b$ и первых $i$ компонент $e$.
| Лемма: |
Каждая их первых $m$ компонент разложения $h$ не больше чем соответствующая компонента из $e$, то есть $ |
</wikitex>
Простое суммирование
<wikitex>| Теорема: |
Пусть $e = \sum^{m}_{i=1}e_i$ и $f = \sum^{n}_{i=1}f_i$ - неперекрывающиеся $m$- и $n$-компонентные разложения, компоненты которых - $p$-битные числа, где $p \geqslant 3$. Предполагается, что компоненты обоих разложений отсортированы в возрастающем порядке, причем все компоненты ненулевые. Тогда следующий алгоритм вернет такое разложение $h$, что $h = \sum^{m + n}_{i=1}h_i = e + f$, где компоненты $h$ также отсортированы в возрастающем порядке и не равны нулю. Алгоритм также сохраняет свойство несмежности/неперекрываемости. |
Псевдокод для суммы:
$ExpansionSum(e, f)$
$1$ $h \Leftarrow e$
$2$ $for$ $i = 1 \dots n$
$3$ $\langle h_i, h_{i+1}, \dots, h_{i+m} \rangle \Leftarrow GrowExpansion(\langle h_i, h_{i+1}, \dots, h_{i+m-1} \rangle, f_i)$
$4$ $return$ $h$
</wikitex>
Быстрое суммирование
<wikitex>В отличие от $\mathrm {ExpansionSum}$, $\mathrm {FastExpansionSum}$ не сохраняет свойства неперекрываемости и несмежности, но гарантирует, что если если входное разложение было строго неперекрывающимся, то на выходе получится разложение с таким же свойством.
| Определение: |
| Разложение называется строго неперекрывающимся, если если его компоненты попарно неперекрываются, ни одна компонента не смежна никаким двум другим, а также любая пара смежных компонент состоит из степеней двойки. |
Например, $11000 + 11$ и $10000 + 1000 + 10 + 1$ — строго неперекрывающиеся разложения, а $11100 + 11$ и $100 + 10 + 1$ — нет.
Для разложения эта характеристика означает, что ноль в записи разложения должен появляться как минимум каждые $p + 1$ бит. Например, разложение, каждая компонента которого есть $p$-битное число, и максимальная величина которой равна $1111$, может быть не больше $1111.01111011110\dots$.
Каждое несмежное разложение является строго неперекрывающимся, а также каждое строго неперекрывающееся разложение есть неперекрывающееся. В общем случае, обратное не верно.
Утверждается, что после предположения о том, что все разложения строго неперекрывающиеся, алгоритм, приведенный ниже, корректно работает на машинах с округлением до ближайшего четного.
| Теорема: |
Пусть $e = \sum^{m}_{i=1}e_i$ и $f = \sum^{n}_{i=1}f_i$ — строго неперекрывающиеся $m$- и $n$-компонентные разложения, компоненты которых — $p$-битные числа, где $p \geqslant 4$. Предполагается, что компоненты обоих разложений отсортированы в возрастающем порядке, причем все компоненты ненулевые. Тогда следующий алгоритм,запущенный на машине с правилом округления до ближайшего четного, вернет такое разложение $h$, что $h = \sum^{m + n}_{i=1}h_i = e + f$, где компоненты $h$ также отсортированы в возрастающем порядке и не равны нулю. Алгоритм также сохраняет свойство несмежности / неперекрываемости. |
Псевдокод для суммы:
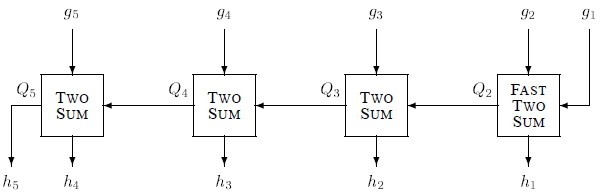
$ExpansionSum(e, f)$
$1$ $Merge$ $e$ $and$ $f$ $into$ $a$ $single$ $sequence$ $g$, $in$ $order$ $of$ $nondecreasing$ $magnitude$ $(possibly$ $with$ $interspersed$ $zeros)$
$2$ $(Q_i, h_1) \Leftarrow FastTwoSum(g_2, g_1)$
$3$ $for$ $i = 3 \dots (n+m)$
$4$ $(Q_i, h_{i-1}) \Leftarrow TwoSum(Q_{i-1}, g_i)$
$5$ $h_{n+m} \Leftarrow Q_{m+n}$
$6$ $return$ $h$
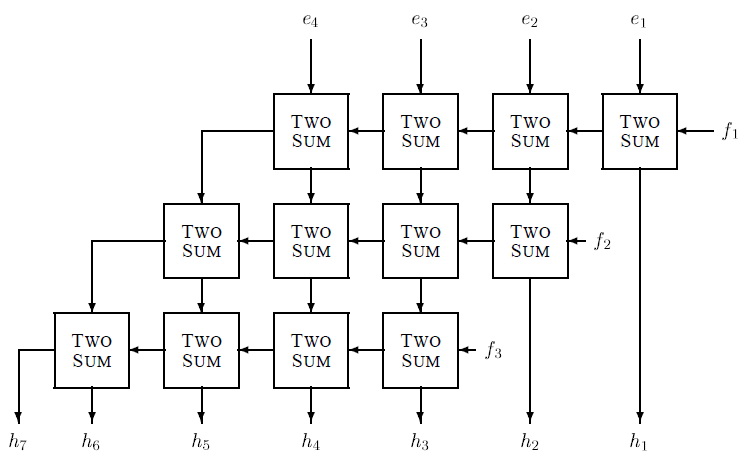
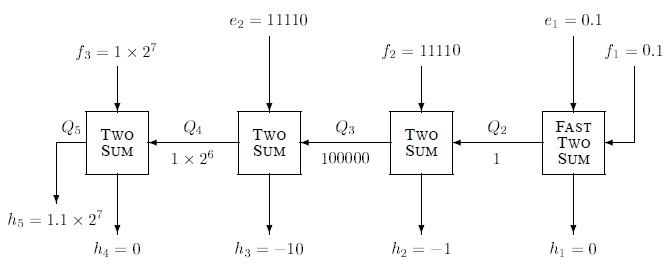
На рисунке ниже показан конкретный пример работы алгоритма
</wikitex>