NP-полнота задач о гамильтоновом цикле и пути в графах

Задача о гамильтоновом цикле в графе

Определение:

[math]\mathrm{[U]HAM}[/math] — язык графов, содержащих [неориентированный] гамильтонов цикл.

Доказательство NP-полноты для ориентированного графа

Для доказательства того, что [math]\mathrm{HAM}[/math] [math]\in[/math] [math]\mathrm{NPC}[/math], необходимо доказать два факта:

• [math]\mathrm{HAM}[/math] [math]\in[/math] [math]\mathrm{NP}[/math]
• [math]\mathrm{HAM}[/math] [math]\in[/math] [math]\mathrm{NPH}[/math]

Доказательство принадлежности к NP

В качестве сертификата возьмем ориентированный гамильтонов цикл в графе [math]G[/math]. Очевидно, он удовлетворяет всем требованиям, налагаемым на сертификат. Проверяющая функция строится очевидным образом, работает за полиномиальное от размера входа время.

Доказательство принадлежности к NPH

Рисунок 1.

Рисунок 2.‎

Рисунок 3.‎

Рисунок 4.

Сведем задачу о выполнимости булевых формул вида [math]\mathrm{3CNF}[/math] к [math]\mathrm{HAM}[/math]. Начнем построение экземпляра [math]\mathrm{HAM}[/math] по булевой формуле в [math]\mathrm{3CNF}[/math]. Пусть формула имеет вид [math]E = e_1 \land e_2 \land \ldots \land e_k[/math], где каждое [math]e_i[/math] — дизъюнкт, представляющий собой сумму трех литералов, скажем, [math]e_i = (\alpha_{i1} \vee \alpha_{i2} \vee \alpha_{i3})[/math]. Пусть [math]x_1, x_2, \ldots, x_n[/math] — переменные в формуле [math]E[/math]. Для всех дизъюнктов и переменных строятся подграфы, как показано на рисунках.

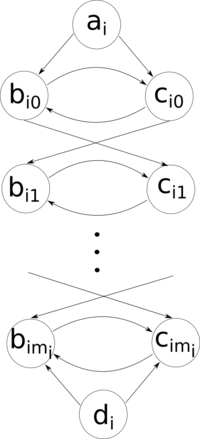
Для каждой переменной [math]x_i[/math] строится подграф [math]H_i[/math] высотой [math]m_i + 2[/math], структура которого показана на рисунке 1. Здесь [math]m_i[/math] — большее из чисел вхождений [math]\bar{x_i}[/math] и [math]x_i[/math] в [math]E[/math]. Узлы [math]c_{ij}[/math] и [math]b_{ij}[/math], расположенные в двух столбцах, соединены между собой дугами в обоих направлениях. Кроме того, каждое [math]b[/math] имеет дугу, ведущую в [math]c[/math], расположенное на ступеньку ниже, т.е., если [math]j \lt m_i[/math], то [math]b_{ij}[/math] имеет дугу, ведущую в [math]c_{i,j+1}[/math]. Аналогично для [math]c_{ij}[/math]. Наконец, есть верхний узел [math]a_i[/math], из которого дуги ведут в [math]b_{i0}[/math] и [math]c_{i0}[/math], и нижний узел [math]d_i[/math], в который ведут дуги из [math]b_{im_i}[/math] и [math]c_{im_i}[/math].

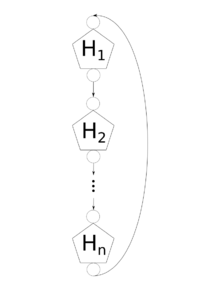
На рисунке 2 показана структура графа в целом. Каждый пятиугольник представляет один подграф, построенный для переменной (его структура показана на рисунке 1. пятиугольники расположены циклически, и из нижнего узла каждого подграфа дуга ведет в верхний узел следующего.

Допустим, граф на рисунке 2 имеет ориентированный гамильтонов цикл. Не ограничивая общности, можно считать, что этот цикл начинается в [math]a_1[/math]. Если затем он переходит в [math]b_{10},[/math], то на следующем шаге он обязательно перейдет в [math]c_{10}[/math] (иначе [math]c_{10}[/math] не появится в цикле). В самом деле, если цикл переходит из [math]a_{1}[/math] в [math]b_{10}[/math], а затем — в [math]c_{11}[/math], то [math]c_{10}[/math] никогда не появится в цикле, поскольку оба его предшественника ([math]a_{0}[/math] и [math]b_{10}[/math]) уже содержатся в нем.

Таким образом, если начало цикла имеет вид [math]a_{1}[/math], [math]b_{10}[/math], то далее он должен спускаться "лесенкой", переходя из стороны в сторону:

[math]a_1, b_{10}, c_{10}, b_{11}, c_{11}, \ldots, d_1[/math].

Если начало цикла имеет вид [math]a_{1}[/math], [math]c_{10}[/math], то в лесенке меняется порядок предшествования [math]c[/math] и [math]b[/math].

[math]a_1, c_{10}, b_{10}, c_{11}, b_{11}, \ldots, d_1[/math].

Решающим пунктом в доказательстве является то, что порядок, при котором спуск совершается от [math]c[/math] к [math]b[/math], можно трактовать как приписывание переменной, соответствующей данному подграфу, значения "истина", а порядок, при котором спуск совершается от [math]b[/math] к [math]c[/math], соответствует приписыванию этой переменной значения "ложь".

Закончив обход подграфа [math]H_1[/math], цикл должен перейти в [math]a_2[/math], где снова возникает выбор следующего перехода — в [math]b_{20}[/math] или в [math]c_{20}[/math]. Однако в силу тех же аргументов, которые приведены для [math]H_1[/math], после того, как сделан выбор направления вправо или влево от [math]a_{2}[/math], путь обхода [math]H_{2}[/math] уже зафиксирован. Вообще, при входе в каждый [math]H_{i}[/math], есть выбор перехода влево или вправо, но никакого другого. Иначе некоторый узел обречен быть недоступным, т.е. он не сможет появиться в ориентированном гамильтоновом цикле, поскольку все его предшественники появились в нем ранее.

В дальнейшем это позволит нам считать, что выбор перехода из [math]a_{i}[/math] в [math]b_{i0}[/math] означает приписывание переменной [math]x_{i}[/math] значения "истина", а перехода в [math]c_{i0}[/math] — значения "ложь". Поэтому граф на рисунке 2 имеет [math]2^n[/math] ориентированных гамильтоновых циклов, соответствующих [math]2^n[/math] возможным подстановкам для [math]n[/math] переменных.

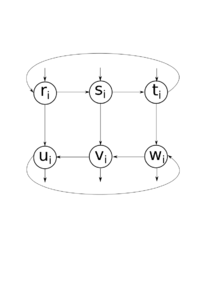
Однако на рисунке 2 изображен лишь скелет графа, порождаемого по формуле [math]E[/math], находящейся в [math]\mathrm{3CNF}[/math]. Каждому дизъюнкту [math]e_{i}[/math] ставится в соответствие подграф [math]I_{j}[/math] (рисунок 3). Он обладает тем свойством, что если цикл входит в [math]r_{j}[/math], то должен выходить из [math]u_{j}[/math]. Аналогично для [math]s, v[/math] и [math]t, w[/math]. В завершение построения графа [math]G[/math] для формулы [math]E[/math] соединяем подграфы [math]I[/math] и [math]H[/math] следующим образом. Допустим, у дизъюнкта [math]e_i[/math] первым литералом является [math]x_i[/math], переменная без отрицания. Выберем некоторый узел [math]c_{ip}[/math], где [math]p[/math] от 0 до [math]m_{i}[/math] -1, ранее не использованный для соединения с подграфами [math]I[/math]. Введем дуги, ведущие из [math]c_{ip}[/math] в [math]r_{j}[/math] и из [math]u_{j}[/math] в [math]b_{i,p+1}[/math]. Если же первым литералом дизъюнкта [math]e_j[/math] является отрицание [math]\bar{x_i}[/math], то нужно отыскать неиспользованный узел [math]b_{ip}[/math], а затем соединить [math]b_{ip}[/math] с [math]r_{j}[/math] и [math]u_{j}[/math] с [math]c_{i,p+1}[/math]

Для второго и третьего литералов [math]e_{j}[/math] граф дополняется точно так же, за одним исключением. Для второго литерала и используются узлы [math]s_{j}[/math] и [math]v_{j}[/math], а для третьего — [math]t_{j}[/math] и [math]w_{j}[/math]. Таким образом, каждый [math]I_{j}[/math] имеет три соединения с подграфами типа [math]H[/math], которые представляют переменные, присутствующие в дизъюнкте [math]e_{j}[/math]. Если литерал не содержит отрицания, то соединение выходит из [math]c[/math]-узла и входит в [math]b[/math]-узел, расположенный ниже, а если содержит — то наоборот.

Мы утверждаем, что построенный таким образом граф [math]G[/math] имеет ориентированный гамильтонов цикл тогда и только тогда, когда формула [math]E[/math] выполнима.

Доказательство достаточности

Предположим, существует подстановка [math]T[/math], удовлетворяющая формуле [math]E[/math]. Построим ориентированный гамильтонов цикл следующим образом.

1. Вначале выберем путь, обходящий только подграфы [math]H[/math] (т.е. граф, изображенный на рисунке 2 в соответствии с подстановкой [math]T[/math]. Таким образом, если [math]T(x_{i}) = 1[/math], то цикл переходит из [math]a_{i}[/math] в [math]b_{i0}[/math], а если [math]T(x_{i}) = 0[/math], то он переходит из [math]a_i[/math] в [math]c_{i0}[/math].
2. Однако цикл, построенный к данному моменту, может содержать дугу из [math]b_{ip}[/math] в [math]c_{i,p+1}[/math], причем у [math]b_{ip}[/math] есть еще одна дуга в один из подграфов в [math]I_{j}[/math], который пока не включен в цикл. Тогда к циклу добавляется "крюк", который начинается в [math]b_{ip}[/math], обходит все шесть узлов подграфа [math]I_{j}[/math] и возвращается в [math]c_{i,p+1}[/math]. Дуга из [math]b_{ip}[/math] в [math]c_{i,p+1}[/math] исключается из цикла, но узлы на ее концах остаются в нем.
3. Аналогично, если в цикле есть дуга из [math]c_{ip}[/math] в [math]b_{i,p+1}[/math] и у [math]c_{ip}[/math] есть еще одна дуга в один из [math]I_{j}[/math], пока не включенных в цикл, то к циклу добавляется "крюк", проходящий через все шесть узлов [math]I_{j}[/math].

Тот факт, что [math]T[/math] удовлетворяет формуле [math]E[/math], гарантирует, что исходный путь, построенный на шаге 1, будет содержать, по крайней мере, одну дугу, которая на шаге 2 или 3 позволит включить в цикл подграф [math]I_j[/math] для каждого дизъюнкта [math]e_i[/math]. Таким образом, цикл включает в себя все подграфы [math]I_j[/math] и является ориентированным гамильтоновым.

Доказательство необходимости

Предположим, что граф [math]G[/math] имеет ориентированный гамильтонов цикл, и покажем, что формула [math]E[/math] выполнима. Напомним два важных пункта из предыдущего анализа.

1. Если гамильтонов цикл входит в некоторый [math]I_j[/math] в узле [math]r_{j}[/math], [math]s_{j}[/math] или [math]t_{j}[/math], то он должен выходить из него в узле [math]u_{j}[/math], [math]v_{j}[/math] или [math]w_{j}[/math] соответственно.
2. Таким образом, рассматривая данный гамильтонов цикл как обход подграфов типа [math]H[/math], можно характеризовать "экскурсию", совершаемую в некоторое [math]I_j[/math], как переход цикла по дуге, "параллельной" одной из дуг [math]b_{ip} \rightarrow c_{i,p+1}[/math] или [math]c_{ip} \rightarrow b_{i,p+1}[/math].

Если игнорировать экскурсии в подграфы [math]I_{j}[/math], то гамильтонов цикл должен быть одним из [math]2^n[/math] циклов, которые возможны с использованием только подграфов [math]H_i[/math] и соответствуют выборам переходов из [math]a_{i}[/math] либо в [math]b_{i0}[/math], либо в [math]c_{i0}[/math]. Каждый из этих выборов соответствует приписыванию значений переменным из [math]E[/math]. Если один из них дает гамильтонов цикл, включающий подграфы [math]I_j[/math], то подстановка, соответствующая этому выбору, должна удовлетворять формуле [math]E[/math].

Причина в том, что если цикл переходит из [math]a_{i}[/math] в [math]b_{i0}[/math], то экскурсия в [math]I_{j}[/math] может быть совершена только тогда, когда [math]j[/math]-й дизъюнкт содержит [math]x_i[/math] в качестве одного из литералов. Если цикл переходит из [math]a_i[/math] в [math]c_{i0}[/math], то экскурсия в [math]I_{j}[/math] может быть совершена только тогда, когда [math]\bar{x_i}[/math] является литералом в [math]j[/math]-ом дизъюнкте. Таким образом, из того, что все подграфы [math]I_j[/math] могут быть включены в граф, следует, что при данной подстановке хотя бы один из литералов в каждом дизъюнкте истинен, т.е. формула [math]E[/math] выполнима.

Доказательство NP-полноты для неориентированного графа

Для доказательства того, что [math]\mathrm{UHAM}[/math] [math]\in[/math] [math]\mathrm{NPC}[/math], необходимо доказать два факта:

• [math]\mathrm{UHAM}[/math] [math]\in[/math] [math]\mathrm{NP}[/math]
• [math]\mathrm{UHAM}[/math] [math]\in[/math] [math]\mathrm{NPH}[/math]

Доказательство принадлежности к NP

В качестве сертификата возьмем гамильтонов цикл в графе [math]G[/math]. Очевидно, он удовлетворяет всем требованиям, налагаемым на сертификат. Проверяющая функция строится очевидным образом, работает за полиномиальное от размера входа время.

Доказательство принадлежности к NPH

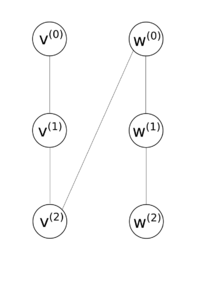
Сведем задачу о гамильтоновом цикле [math]\mathrm{HAM}[/math] к [math]\mathrm{UHAM}[/math]. Пусть дан ориентированный граф [math]G[/math]. Построим по нему неориентированный граф [math]H[/math]. Для этого каждой вершине из графа [math]G[/math] поставим в соответствие 3 вершины в графе [math]H[/math], соединив в [math]H[/math] ребром первую получившуюся со второй, а вторую — с третьей. Для каждой дуги, инцидентной исходной вершине в [math]G[/math] поставим в соответствие ребро в [math]H[/math]. В случае, если дуга исходит из этой вершины, то соединим ребро с последней из получившихся вершин в [math]H[/math], а если она входит в вершину, то соединим с первой из получившихся (см. рисунок 4). Таким образом, в построенном графе [math]H[/math] гамильтонов путь будет тогда и только тогда, когда в исходном графе [math]G[/math] будет ориентированный гамильтонов путь.

Задача о гамильтоновом пути в графе

Определение:

[math]\mathrm{[U]HAMP}[/math] — язык графов, содержащих [неориентированный] гамильтонов путь.

Доказательство NP-полноты для ориентированного графа

Для доказательства того, что [math]\mathrm{HAMP}[/math] [math]\in[/math] [math]\mathrm{NPC}[/math], необходимо доказать два факта:

• [math]\mathrm{HAMP}[/math] [math]\in[/math] [math]\mathrm{NP}[/math]
• [math]\mathrm{HAMP}[/math] [math]\in[/math] [math]\mathrm{NPH}[/math]

Доказательство принадлежности к NP

В качестве сертификата возьмем ориентированный гамильтонов путь в графе [math]G[/math]. Очевидно, он удовлетворяет всем требованиям, налагаемым на сертификат. Проверяющая функция строится очевидным образом, работает за полиномиальное от размера входа время.

Доказательство принадлежности к NPH

Сведем задачу об ориентированном гамильтоновом цикле [math]\mathrm{HAM}[/math] к [math]\mathrm{HAMP}[/math]. Пусть дан граф [math]G[/math]. Выберем произвольную вершину графа [math]G[/math] и раздвоим ее, и входящие дуги направим в одну из полученных вершин, а исходящие пустим из другой. Теперь, если в исходном графе был ориентированный гамильтонов цикл, то в полученном будет ориентированный гамильтонов путь. В обратную сторону, если в полученном графе будет ориентированный гамильтонов путь, то на первом и последнем местах в этом пути окажутся новые вершины, соответствующие раздвоенной, поскольку ни одна из них не может оказаться в середине пути (у неё есть либо входящие, либо исходящие дуги). Таким образом, если в полученном графе будет гамильтонов путь, то в исходном графе [math]G[/math] был гамильтонов цикл.

Доказательство NP-полноты для неориентированного графа

Для доказательства того, что [math]\mathrm{UHAMP}[/math] [math]\in[/math] [math]\mathrm{NPC}[/math], необходимо доказать два факта:

• [math]\mathrm{UHAMP}[/math] [math]\in[/math] [math]\mathrm{NP}[/math]
• [math]\mathrm{UHAMP}[/math] [math]\in[/math] [math]\mathrm{NPH}[/math]

Доказательство принадлежности к NP

В качестве сертификата возьмем гамильтонов путь в графе [math]G[/math]. Очевидно, он удовлетворяет всем требованиям, налагаемым на сертификат. Проверяющая функция строится очевидным образом, работает за полиномиальное от размера входа время.

Доказательство принадлежности к NPH

Сведем задачу о гамильтоновом пути в ориентированном графе [math]\mathrm{HAMP}[/math] к [math]\mathrm{UHAMP}[/math]. Пусть дан ориентированный граф [math]G[/math]. Построим по нему неориентированный граф [math]H[/math]. Для этого каждой вершине из графа [math]G[/math] поставим в соответствие 3 вершины в графе [math]H[/math], соединив в [math]H[/math] ребром первую получившуюся со второй, а вторую — с третьей. Для каждой дуги, инцидентной исходной вершине в [math]G[/math] поставим в соответствие ребро в [math]H[/math]. В случае, если дуга исходит из этой вершины, то соединим ребро с последней из получившихся вершин в [math]H[/math], а если она входит в вершину, то соединим с первой из получившихся. Таким образом, в построенном графе [math]H[/math] гамильтонов путь будет тогда и только тогда, когда в исходном графе [math]G[/math] будет ориентированный гамильтонов путь.

См. также

• NP
• NPH
• NPC
• Классы NP и Σ₁
• 3CNFSAT
• Примеры NP-полных языков
• Задача о коммивояжере

Источники информации

• Ахо, Альфред, В., Хопкрофт, Джон, Ульман, Джеффри, Д. "Структуры данных и алгоритмы" — Издательский дом «Вильямс», 2000. — С. 384. — ISBN 5-8459-0122-7 (рус.) / ISBN 0-201-00023-7 (англ.)
• Хопкрофт Дж., Мотвани Р., Ульман Дж. Введение в теорию автоматов, языков и вычислений. 2-е издание. — М.: Издательский дом "Вильямс", 2002. — 528 с. — ISBN 5-8459-0261-4 (рус.)