Quotient filter
Quotient filter — вероятностное множество.
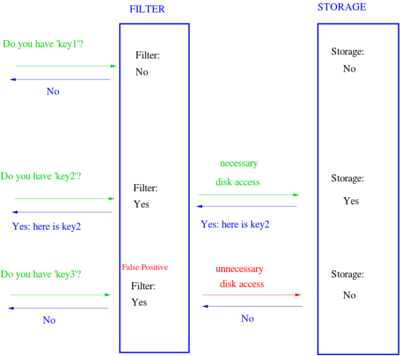
Существует связь между размером хранилища и шансом ложноположительного срабатывания. Поддерживаются операции добавления нового элемента в множество. С увеличением размера хранимого множества повышается вероятность ложного срабатывания. Структуру разработал Michael Bender в 2011 году[1] как замена фильтра Блума. Фильтр используется для ускорения ответов в хранилище ключ-значение.
Описание структуры данных
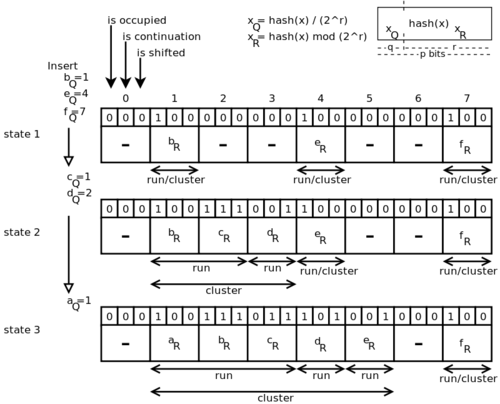
В quotient filter хеш-функция возвращает битовый хеш, последние бит которого называются остатком (англ. remainder), а старших бит называются частным (англ. quotient), отсюда название структуры quotient filter[2]. Фильтр представляет собой хеш-таблицу, в которой харанится остаток и бита дополнительной информации (удобно хранить в целочисленном типе, используя старших бита под дополнительную информацию, а оставшиеся биты под остаток, накладывает ограничение на размер остатка). Биты дополнительной информации используются для разрешения ситуации, когда частное различных ключей указывает на одну ячейку в хеш-таблице. Размер хеш-таблицы составляет , так как есть всего разных частных.
Пусть у нас есть ключ , его хеш обозначим , остаток и частное . Попробуем поместить остаток в хеш-таблицу в ячейку с индексом , называемую канонической. Возможно, ячейка уже занята, так как существует шанс полных коллизий (остаток и частное разных ключей совпадают) или частичных коллизий (частное разных ключей совпадают). При полной коллизии мы получим ложноположительное срабатывание, но при частичной коллизии, с помощью дополнительных битов это избегается. Когда каноническая ячейка занята, помещаем остаток в какую-то ячейку справа. Этот способ решения колизий схож с линейным методом разрешения колизий.
Последовательность ячеек, имеющих одинаковые частные называется пробегом (англ. run). Возможно, что начало пробега не занимает канонический слот, если он уже занят каким-то другим пробегом.
Пробег, у которого первый элемент занимает каноническую ячейку, является началом кластера. Кластер — объединение последовательных пробегов, концом кластера является пустая ячейка или начало другого кластера.
Три дополнительных бита имеют следующие функции:
- бит занятости — равен единице, если ячейка является канонической для некого ключа в фильтре, сохраненого необязательно в этой ячейке,
- бит продолжения — равен единице, если ячейка занята, но не первым элементов пробеге,
- бит сдвига — равен единице, если пробег сдвинут относительно канонического слота.
| Бит занятости | Бит Продолжения | Бит сдвига | Описание |
|---|---|---|---|
| 0 | 0 | 0 | Пустая ячейка. |
| 0 | 0 | 1 | Ячейка содержит начало пробега, сдвинутого относительно канонического слота. |
| 0 | 1 | 0 | Не используется. |
| 0 | 1 | 1 | Ячейка содержит элемент пробега (не первый), сдвинутого относительно канонического слота. |
| 1 | 0 | 0 | Ячейка содержит первый элемет пробега в его каноническом слоте. |
| 1 | 0 | 1 | Ячейка содержит первый элемет пробега, сдвинутого относительно канонического слота. Ячейка является канонической, для существующего пробега сдвинутого вправо. |
| 1 | 1 | 0 | Не используется. |
| 1 | 1 | 1 | Ячейка содержит элемент пробега (не первый), сдвинутого относительно канонического слота. Ячейка является канонической, для существующего пробега сдвинутого вправо. |
Поиск
Пусть мы ищем ключ . Смотрим в ячейку с индексом , это каноническая ячейка для частного . Если в этой ячейке бит занятости не единица, то элемент точно не содержится в множестве. Если бит занятости единица, то нам нужно найти пробег для . Так как начало нужного пробега может быть сдвинуто, найдем начало кластера. Идем влево от ячейки с индексом и ищем первую с битом сдвига равным нулю, эта ячейка и будет началом кластера. Пока мы идем влево от ячейки с индексом будем поддерживать счетчик, который бедет показывать сколько пробегов нам нужно будет пропустить от начала кластера. Каждая ячейка с битом занятости равным единице увеличивает счетчик на . После того как мы нашли начало кластера, пойдем от него вправо, каждая ячейка с битом продолжения равным нулю говорит о завершении пробега, когда счетчик станет равным нулю мы найдем нужный нам пробег для частного . Если в этом пробеге содержится , то , вероятно, содержится в множестве, иначе точно не содержится в множестве.
Вставка
Аналогично с поиском: найдем позицию для , сдвигаем на одну позицию влево все эллементы кластера, начиная с выбранного, обновляем дополнительные биты.
- Сдвиг не влияет на бит занятости. Выставляем бит занятости в ячейке в единицу.
- Если мы вставляем в начало пробега, следовательно предыдущий элемент пробега стал вторым, у него нужно выставить бит продолжения.
- Мы выставляем бит сдвига в единицу для каждой ячейки, что мы сдвинули.
Преимущества
- Последовательное расположение данных. Можно загружать только кластер, уменьшая количество кеш промахов.
- Простое увеличение или уменьшение хеш-таблицы, достаточно перенести один бит из остатка в частное или наоборот.
- Простое слияние двух фильтров.
См. также
Примечания
- ↑ Bender, Michael A.; Farach-Colton, Martin; Johnson, Rob; Kuszmaul, Bradley C.; Medjedovic, Dzejla; Montes, Pablo; Shetty, Pradeep; Spillane, Richard P.; Zadok, Erez (June 2011)."Don't thrash: how to cache your hash on flash" (PDF)
- ↑ Knuth, Donald (1973). The Art of Computer Programming:Searching and Sorting, volume 3. Section 6.4, exercise 13: Addison Wesley