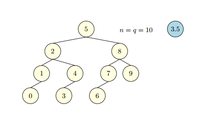
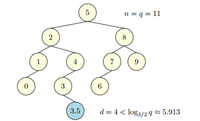
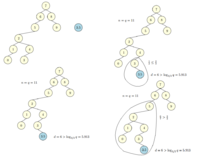
Scapegoat Tree
Scapegoat Tree — структура данных, представляющая собой частично сбалансированное дерево поиска (степень сбалансированности может быть настроена), такое что операции поиска, вставки и удаления работают за O(log n), при этом скорость одной операции может быть улучшена в ущерб другой.
Содержание
Идея
При работе необходимо поддерживать состояние сбалансированного дерева, иначе время работы операции поиска может превысить .
Степень сбалансированности
Будем считать, что дерево является сбалансированным, если выполняются следующее: Введем коэффициент , который показывает, насколько дерево может быть несбалансированным. Математически это выглядит следующим образом: ; ; , где и — размер левого и правого поддерева вершины .
Плюсы
- Данное дерево позволяет ускорить одни операции взамен на ускорение других, что отличает его от других (простое бинарное дерево, красно-черное дерево, splay-дерево). Результаты исследований показывают, что Scapegoat tree работает на случайных данных быстрее, чем красно-черное.
- Требует меньше памяти, так как не надо хранить дополнительную информацию в вершине для балансировки.
- Настройки скорости можно менять в процессе выполнения программы.
Минусы
- Данное дерево сложно для написания.
- В случае неправильной настройки скорости работы дерево будет проигрывать по скорости работы другим.
Если условие нарушается, запускается операция перебалансировки дерева. Заметим, что при деревом будет считаться даже линейная структура.
Примечание: Существует два подхода к балансу дерева, которые дают похожий результат. Первый — задавать . Второй — задать ограничение , большее чем число элементов в дереве (чем больше ограничение, тем более несбалансированным может быть дерево), и следить, чтобы был больше максимальной глубины дерева. В противном случае, необходимо произвести перебалансировку дерева.
Свойства
Данная структура обладает следующими свойствами:
- Выбор коэффициента позволяет ускорить некоторые операции. Например, выбор большого значения позволит выполнять очень много операций вставки, но замедлит операции поиска. При этом выбор коэффициента можно выполнять в процессе выполнения, опираясь на входные данные. Однако, неправильный выбор приводит к сильному увеличению времени работы.
- Не требуется проводить перебалансировку дерева при поиске, что гарантирует максимальное время работы поиска .
- В некоторых случаях операции модификации занимают , хотя из амортизированная сложность - .
- За счет отсутствия необходимости хранить дополнительные данные в вершинах данное дерево оптимальнее остальных по памяти.
Структура
Структура вершины n
n.key — значение в вершине n.left — левый ребенок вершины n.right — правый ребенок вершины n.height — высота поддерева данной вершины n.depth — глубина вершины n.parent — ссылка на родителя n.sibling — ссылки на "братьев" данной вершины
Структура дерева T
T.root — ссылка на корень дерева
T.size — число вершин в дереве
T.maxSize — максимальное число вершин в дереве после последней перебалансировки
T.hα — вспомогательное значение, вычисляется как:
T.height — высота дерева
Операции
Поиск
- — корень дерева или поддерева, в котором происходит поиск.
- — искомый ключ в дереве.
Search(root, k):
if root = null or root.key = k:
return root
else if k ≤ root.left.key:
return Search(root.left, k)
else:
return Search(root.right, k)
Вставка элемента
Пока дерево остается -сбалансированным, выполняем модифицированную вставку элемента в дерево, которая аналогична обычной вставке в двоичное дерево, но операция будет возвращать глубину данной вершины. В тот момент, когда дерево стало несбалансированным, надо начать поиск вершины, которая нарушает условие сбалансированности. Для этого надо пройти по дереву вверх. Только что вставленная вершина ей быть не может. После нахождения этой вершины надо запустить операцию перебалансировки.
Нам нужна специальная функция , которая позволяет найти тот элемент дерева, который испортил баланс (именно из-за этой процедуры дерево так называется. Scapegoat - "козел отпущения", который испортил баланс).
- — узел дерева. Обычно, процедура вызывается от только что добавленной вершины.
FindScapegoat(n):
size = 1
height = 0
while (n.parent <> null):
height = height + 1
totalSize = 1 + size + n.sibling.size()
if height > ⌊log1/α(totalSize)⌋:
return n.parent
n = n.parent
size = totalSize
Сама вставка элемента:
- — ключ, который будет добавлен в дерево.
Insert(k):
height = InsertKey(k)
if height = −1:
return false;
else if height > T.hα:
scapegoat = FindScapegoat(Search(T.root, k))
RebuildTree(n.size(), scapegoat)
return true
Удаление элемента элемента
Сначала надо удалить вершину, как в обычном двоичном дереве. Потом надо проверить дерево на сбалансированность. Если дерево осталось сбалансированным, ничего делать не надо. В противном случае надо начать перебалансировку дерева.
Функция DeleteKey(k) удаляет элемент, аналогично удалению в бинарном дереве, и возвращает глубину удаленного элемента.
- — ключ, который будет удален.
Delete(k):
deleted = DeleteKey(k)
if deleted:
if T.size < (T.α · T.maxSize):
RebuildTree(T.size, T.root)
Перебалансировка дерева
Общая идея процедуры выглядит следующим образом: сначала из исходного дерева мы получаем список вершин в неубывающем порядке, при этом вершина стоит в списке перед детьми. После этого мы создаем новое дерево из списка.
Получение списка
- — корень дерева, которое будет преобразовано в список.
FlattenTree(root, head):
if root = null:
return head
root.right = FlattenTree(root.right, head)
return FlattenTree(root.left, root)
Построение дерева
- — число вершин в списке.
- — первая вершина в списке.
BuildHeightBalancedTree(size, head):
if size = 1 then:
return head
else if size = 2 then:
(head.right).left = head
return head.right
root = (BuildHeightBalancedTree(⌊(size − 1)/2⌋, head)).right
last = BuildHeightBalancedTree(⌊(size − 1)/2⌋, root.right)
root.left = head
return last
Перестроение дерева
- — число вершин в поддереве.
- — вершина, которая испортила баланс.
RebuildTree(size, scapegoat):
head = FlattenTree(scapegoat, null)
BuildHeightBalancedTree(size, head)
while head.parent!=null do
head = head.parent
return head