Smoothsort
Плавная сортировка (англ. Smooth sort) — алгоритм сортировки, модификация сортировки кучей, разработанный Э. Дейкстрой. Как и пирамидальная сортировка, в худшем случае работает за время . Преимущество плавной сортировки в том, что её время работы приближается к , если входные данные частично отсортированы, в то время как у сортировки кучей время работы не зависит от состояния входных данных.
Содержание
Основная идея
Разовьём идею пирамидальной сортировки. Для этого используем не двоичную кучу, а специальную, полученную с помощью чисел Леонардо[1], которые задаются следующим образом:
Вот первые несколько членов этой последовательности:
| Утверждение: |
Любое натуральное число представимо в виде суммы различных чисел Леонардо. |
| Утверждение: |
, где — -ое число Фибоначчи. |
| Это утверждение доказывается по индукции. База: . Пусть для первых чисел это равенство выполняется. Делаем индуктивный переход: . Утверждение доказано. |
| Определение: |
K-ая куча Леонардо — это двоичное дерево с количеством вершин , удовлетворяющее следующим условиям:
|
Можно заметить, что куча Леонардо очень похожа на биномиальную.
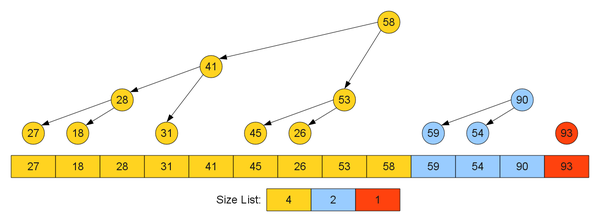
Будем поддерживать следующий инвариант:
- сортируемый массив делится на группу подмассивов,
- каждый подмассив представляет собой структуру данных куча,
- каждая куча имеет размер равный одному из чисел Леонардо,
- размеры куч строго убывают слева направо,
- при этом не существует двух куч, имеющих одинаковый размер,
- значения ключей в корнях деревьев идут в порядке возрастания слева направо,
- в самих кучах значение в детях меньше либо равно значению в родителе.
В дальнейшем эту группу подмассивов будем называть последовательностью куч.
Алгоритм:
Шаг 0: В массиве записаны элементы, которые надо отсортировать.
Шаг 1: Превращение массива в последовательность куч.
Шаг 2: Пока последовательность куч не пустая, достаем максимальный элемент (это всегда корень самой правой кучи) и восстанавливаем порядок куч, который мог измениться.
Операции над последовательностью куч
При конструировании последовательности куч будем по очереди вставлять в конец новые элементы, а при получении отсортированного массива — удалять максимальный элемент из последовательности. Следовательно, нам необходимы две операции: увеличение последовательности куч путём добавления элемента справа (будем считать, что в начале последовательности располагаются кучи максимального размера) и уменьшение путём удаления крайнего правого элемента (корня последней кучи), с сохранением состояния кучи и последовательности.
Чтобы быстро обращаться к кучам, будем хранить список их длин. Зная индекс корня некоторой кучи и её длину, можно найти индекс корня кучи слева от неё. Чтобы искать индексы детей вершины, надо воспользоваться свойством кучи Леонардо, что левым поддеревом является -ая, а правым является -ая куча Леонардо. Для хранения списка длин куч придется выделить дополнительной памяти.
Вставка элемента
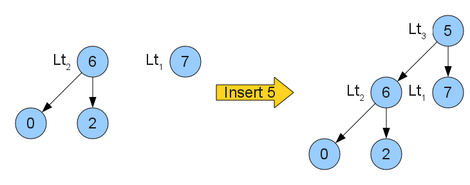
При добавлении в последовательность нового элемента возможны две ситуации:
- Если две последние кучи имеют размеры и (двух последовательных чисел Леонардо), новый элемент становится корнем кучи большего размера, равного . Для неё свойство кучи необязательно.
- Если размеры двух последних куч не равны двум последовательным числам Леонардо, новый элемент образует новую кучу размером . Этот размер полагается равным , кроме случая, когда крайняя правая куча уже имеет размер , тогда размер новой одноэлементной кучи полагают равным .
После этого необходимо восстановить свойства кучи и последовательности куч, что, как правило, достигается при помощи разновидности сортировки вставками (см. ниже псевдокод):
- Крайняя правая куча (сформированная последней) считается «текущей» кучей.
- Пока слева от неё есть куча, и значение её корня больше значения текущего корня и обоих корней куч-потомков:
- Меняются местами новый корень и корень кучи слева (это гарантирует выполнение инварианта для текущей кучи). И куча, с которой произошел обмен, становится текущей.
- Потом выполняется «просеивание» кучи, на которой остановилась сортировка корней, чтобы гарантировать выполнение инварианта кучи:
- Пока размер текущей кучи больше , и значение корня любой из куч-потомков больше значения корня текущей кучи:
- Меняются местами наибольший по значению корень кучи-потомка и текущий корень. Куча-потомок становится текущей кучей.
- Пока размер текущей кучи больше , и значение корня любой из куч-потомков больше значения корня текущей кучи:
Просеивание в куче Леонардо сильно упрощено, так как каждая куча будет иметь либо двух потомков, либо ноль. Нет нужды беспокоиться об отсутствии одной из куч-потомков.
Так как в последовательности куч, то модификация сортировки вставками будет работать за . Просеивание тоже выполняется за , тогда в итоге операция вставки выполняется за: .
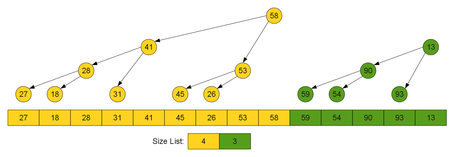
Уменьшение последовательности куч путём удаления элемента справа
Если размер крайней правой кучи равен (то есть или ), эта куча просто удаляется. В противном случае корень этой кучи удаляется, кучи-потомки считаются элементами последовательности куч, после чего проверяется выполнение свойства последовательности куч (т.е. корни деревьев идут в порядке возрастания слева направо), сначала для левой кучи, затем — для правой.
Так как в последовательности куч, то восстановление свойства последовательности выполняется за .
Восстановление свойств последовательности
Пусть нам надо восстановить инвариант последовательности куч. Будем считать, что функции (возвращает индекс корня ближайшей слева кучи), (возвращает индекс левого сына), (возвращает индекс правого сына) уже реализованы. В функцию передается индекс корня кучи, с которой начинаем восстановление.
function ensureSequence(i: int):
j = prev(i) // j - индекс корня соседней кучи
while A[j] > A[i] and A[j] > A[left(i)] and A[j] > A[right(i)]
swap(A[j], A[i])
i = j
j = prev(i)
siftDown(i)
Сложность
Построение последовательности
Последовательность куч получается при вставке элементов массива по очереди в эту самую последовательность. Получаем время работы .
Получение отсортированного массива
Так как удаление максимального элемента из последовательности выполняется за , то время работы сортировки составляет .
Лучший случай
Однако если подать на вход плавной сортировке уже отсортированный массив, асимптотика будет составлять . Дело в том, что:
- Операция добавления элемента последовательности на таком примере будет выполняться за , из-за того, что в конец будет добавляться максимальный элемент и просеивание будет сразу останавливаться.
- Операция получения и удаления максимального элемента будет также выполняться за , потому что в силу построения в корнях куч-детей будут новые максимальные элементы и следовательно восстановление свойства последовательности закончится на просмотре корня соседней кучи.
В итоге на таком примере получается асимптотика .
Достоинства
- худшее время работы — ,
- время работы в случае, когда подается отсортированный массив — .
Недостатки
- не является устойчивой,
- требует дополнительной памяти для хранения длин куч в последовательности. Однако с помощью некоторых модификаций расходы на дополнительную память можно сократить до .
Связь с быстрой сортировкой
На практике, когда реализуют алгоритм быстрой сортировки, пытаются улучшить асимптотику в худшем случае. Для этого заводится некоторый лимит глубины рекурсии, при превышении которого запускают другую сортировку. Так реализована сортировка в стандартной библиотеке языка С++. Часто при превышении порога глубины рекурсии используют сортировку кучей. Замена неё на плавную сортировку могла бы улучшить время работы на некоторых тестах, так как после нескольких итераций быстрой сортировки массив окажется почти отсортированным, а на таких массивах время работы плавной сортировки приближается к линейному. Хотя итоговой линейной асимптотики достичь всё равно не получится по теореме о нижней оценке.