Динамическое программирование — различия между версиями
Borisov (обсуждение | вклад) |
Borisov (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
==Оптимальная подструктура== | ==Оптимальная подструктура== | ||
| − | [[Файл: | + | [[Файл:FG.png|150px|thumb|Граф подзадач для чисел Фибоначчи]] |
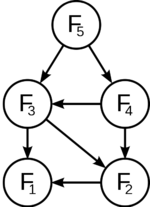
Задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе [[Кратчайший_путь_в_ациклическом_графе|кратчайшего пути]] от одной вершины к другой. | Задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе [[Кратчайший_путь_в_ациклическом_графе|кратчайшего пути]] от одной вершины к другой. | ||
| − | Задача по нахождению кратчайшего пути между некоторыми вершинами графа | + | Задача по нахождению кратчайшего пути между некоторыми вершинами графа содержит в себе оптимальное решение подзадач. Это свойство называется оптимальной подструктурой. Наличие у задачи этого свойства определяет её решаемость динамическим программированием. |
| + | [[Файл:ULP.JPG|thumb|left|150px|Задача о самом длинном невзвешенном пути]] | ||
| + | Иногда оптимальная структура может отсутствовать в задаче. | ||
| + | Рассмотрим задачу, в которых имеется ориентированный граф $G = (V, E)$ и вершины $u, v \in V$, задачу по определению простого пути от вершины $u$ к вершине $v$, состоящий из максимального количества рёбер. | ||
| + | |||
| + | Рассмотрим путь $q \rightarrow r \rightarrow t$, который является самым длинным простым путем $q \rightsquigarrow t$. Является ли путь $q \rightarrow r$ самым длинным путем $q \rightsquigarrow r$? Нет, поскольку простой путь $q \rightarrow s \rightarrow t \rightarrow r$ длиннее. Является ли путь $r \rightarrow t$ самым длинным путем $r \rightsquigarrow t$? Снова нет, поскольку простой путь $r \rightarrow q \rightarrow s \rightarrow t$ длиннее. | ||
| + | Таким образом, в задаче о поиске самого длинного невзвешенного пути не возникает никаких оптимальных подструктур. Для этой задачи до сих пор не найдено ни одного эффективного алгоритма, работающего по принципу динамического программирования. Фактически, это NP-полная задача, т.е. вряд ли ее можно решить в течение полиномиального времени. | ||
| + | |||
| + | |||
| + | |||
==Оптимальность для подзадач== | ==Оптимальность для подзадач== | ||
| Строка 19: | Строка 28: | ||
==Принцип оптимальности для динамического программирования на префиксе== | ==Принцип оптимальности для динамического программирования на префиксе== | ||
| − | [[Файл:ST.jpg| | + | [[Файл:ST.jpg|200px|thumb|left]] |
Рассмотрим принцип оптимальности для динамического программирования на префиксе. | Рассмотрим принцип оптимальности для динамического программирования на префиксе. | ||
| − | Задан граф. Требуется дойти от $S$ до $T$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Есть какой-то префикс, оптимальный путь проходит через $U$. Рассмотрим префикс $\Delta U$ (т.е. путь $S \rightsquigarrow U$), пусть он неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$, а путь $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. | + | Задан граф. Требуется дойти от некоторой начальной вершины $S$ до конечной $T$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Есть какой-то префикс, оптимальный путь проходит через $U$. Рассмотрим префикс $\Delta U$ (т.е. путь $S \rightsquigarrow U$), пусть он неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$, а путь $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. |
</wikitex> | </wikitex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
==Ссылки== | ==Ссылки== | ||
*Лекция 10.11.2011 | *Лекция 10.11.2011 | ||
| − | + | *Т. Кормен. «Алгоритмы. Построение и анализ» (второе издание, Глава 15) | |
| − | *Т. Кормен. «Алгоритмы. Построение и анализ» ( | + | *T. H. Cormen. «Introduction to Algorithms» (third edition, Chapter 15) |
| − | *T. H. Cormen. «Introduction to Algorithms» ( | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Динамическое программирование]] | [[Категория:Динамическое программирование]] | ||
Версия 04:58, 30 ноября 2011
<wikitex>
Содержание
Процесс разработки алгоритмов динамического программирования
В процессе составления алгоритмов динамического программирования, требуется следовать последовательности из четырёх действий:
- Описать структуру оптимального решения
- Рекурсивно определить значение оптимального решения
- Вычислить значение оптимального решения с помощью метода восходящего анализа
- Составить оптимального решения на основе полученной информации
Оптимальная подструктура
Задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе кратчайшего пути от одной вершины к другой.
Задача по нахождению кратчайшего пути между некоторыми вершинами графа содержит в себе оптимальное решение подзадач. Это свойство называется оптимальной подструктурой. Наличие у задачи этого свойства определяет её решаемость динамическим программированием.
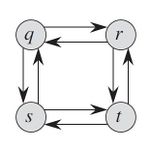
Иногда оптимальная структура может отсутствовать в задаче. Рассмотрим задачу, в которых имеется ориентированный граф $G = (V, E)$ и вершины $u, v \in V$, задачу по определению простого пути от вершины $u$ к вершине $v$, состоящий из максимального количества рёбер.
Рассмотрим путь $q \rightarrow r \rightarrow t$, который является самым длинным простым путем $q \rightsquigarrow t$. Является ли путь $q \rightarrow r$ самым длинным путем $q \rightsquigarrow r$? Нет, поскольку простой путь $q \rightarrow s \rightarrow t \rightarrow r$ длиннее. Является ли путь $r \rightarrow t$ самым длинным путем $r \rightsquigarrow t$? Снова нет, поскольку простой путь $r \rightarrow q \rightarrow s \rightarrow t$ длиннее. Таким образом, в задаче о поиске самого длинного невзвешенного пути не возникает никаких оптимальных подструктур. Для этой задачи до сих пор не найдено ни одного эффективного алгоритма, работающего по принципу динамического программирования. Фактически, это NP-полная задача, т.е. вряд ли ее можно решить в течение полиномиального времени.
Оптимальность для подзадач
Важнейшее свойство задач, которое позволяет решать их с помощью динамического программирования, это оптимальность для подзадач. В зависимости от формулировки задачи, будь то динамическое программирование на отрезке, на префиксе, на дереве, термин оптимальности для подзадач может быть различным, но, в целом, формулируется так:
| Определение: |
| «Если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом» |
Принцип оптимальности для динамического программирования на префиксе
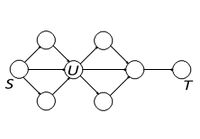
Рассмотрим принцип оптимальности для динамического программирования на префиксе.
Задан граф. Требуется дойти от некоторой начальной вершины $S$ до конечной $T$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Есть какой-то префикс, оптимальный путь проходит через $U$. Рассмотрим префикс $\Delta U$ (т.е. путь $S \rightsquigarrow U$), пусть он неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$, а путь $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. </wikitex>
Ссылки
- Лекция 10.11.2011
- Т. Кормен. «Алгоритмы. Построение и анализ» (второе издание, Глава 15)
- T. H. Cormen. «Introduction to Algorithms» (third edition, Chapter 15)