Динамическое программирование
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А.Кумок
Содержание
Процесс разработки алгоритмов динамического программирования
В процессе составления алгоритмов динамического программирования, требуется следовать последовательности из четырёх действий:
- Описать структуру оптимального решения.
- Рекурсивно определить значение оптимального решения.
- Вычислить значение оптимального решения с помощью метода восходящего анализа.
- Составить оптимальное решение на основе полученной информации.
Оптимальная подструктура
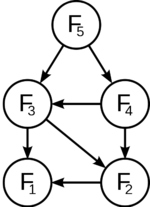
Задача имеет оптимальную подструктуру, если её оптимальное решение может быть рационально составлено из оптимальных решений её подзадач.Наличие оптимальной подструктуры в задаче используется для определения применимости динамического программирования и жадных алгоритмов для решения оной. Например, задача по нахождению кратчайшего пути между некоторыми вершинами графа содержит в себе оптимальное решение подзадач.
Многие задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе кратчайшего пути от одной вершины к другой.
Отсутствие оптимальной подструктуры
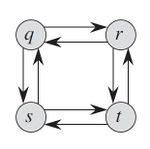
Иногда оптимальная подструктура может отсутствовать в задаче. Рассмотрим задачу, в которой имеется ориентированный граф $G = (V, E)$ и вершины $u, v \in V$, задачу по определению простого пути от вершины $u$ к вершине $v$, состоящий из максимального количества рёбер.
Рассмотрим путь $q \rightarrow r \rightarrow t$, который является самым длинным простым путем $q \rightsquigarrow t$. Является ли путь $q \rightarrow r$ самым длинным путем $q \rightsquigarrow r$? Нет, поскольку простой путь $q \rightarrow s \rightarrow t \rightarrow r$ длиннее. Является ли путь $r \rightarrow t$ самым длинным путем $r \rightsquigarrow t$? Снова нет, поскольку простой путь $r \rightarrow q \rightarrow s \rightarrow t$ длиннее. Таким образом, в задаче о поиске самого длинного невзвешенного пути не возникает никаких оптимальных подструктур. Для этой задачи до сих пор не найдено ни одного эффективного алгоритма, работающего по принципу динамического программирования. Фактически, это NP-полная задача, т.е. вряд ли ее можно решить в течение полиномиального времени.
Оптимальность для подзадач
Важнейшее свойство задач, которое позволяет решать их с помощью динамического программирования, это оптимальность для подзадач. В зависимости от формулировки задачи, будь то динамическое программирование на отрезке, на префиксе, на дереве, термин оптимальности для подзадач может быть различным, но, в целом, формулируется так: если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом.
Принцип оптимальности на префиксе
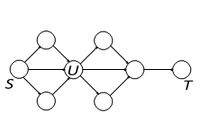
Рассмотрим некий необратимый процесс производства и представим его в виде ориентированного и ациклического графа. Процесс проходит некий ряд состояний. Началом производства (первым состоянием) обозначим вершину графа $S$, а конец производства (последнее состояние) $T$. Процесс требует оптимизации, т.е. требуется найти оптимальный путь $S \rightsquigarrow T$. Он проходит через вершину графа $U$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Теперь рассмотрим принцип оптимальности для динамического программирования на префиксе. Итак, имеем некоторый оптимальный путь $S \rightsquigarrow T$, который проходит через $U$. Пусть префикс $ \Delta U$, т.е. путь от $S \rightsquigarrow U$, неоптимален. Тогда заменим неоптимальную часть $S \rightsquigarrow U$ пути $S \rightsquigarrow T$ оптимальной, а путь $U \rightsquigarrow T$ добавим в конец. Получим оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. Т.е. чтобы получить оптимальный путь из одной вершины графа в другую, префиксы меньших путей должны быть оптимальными.
В качестве примера рассмотрим следующую задачу: пусть дан ациклический ориентированный взвешенный граф, требуется найти вес кратчайшего пути из u в v. Воспользуемся принципом оптимальности на префиксе.
Пусть — функция, где — вес кратчайшего пути из в . Ясно, что равен . Пусть — вес ребра из в . Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:
Так как мы обходим граф в порядке топологической сортировки, то на -ом шаге всем ( такие, что существует ребро из в ) уже присвоены оптимальные ответы, и, следовательно, также будет присвоен оптимальный ответ.
Примеры задач
Принцип оптимальности на подотрезках
Требуется посчитать функцию $f(1, n)$. Принцип состоит в следующем: пусть для всех отрезков $i$, $j$ (где ) известен оптимальный ответ для функции $f(i, j)$. Тогда мы будем вычислять $f(u, v)$ через такие $f(i, j)$. В качестве примера рассмотрим следующую классическую задачу: дана строка длины n, нужно найти максимальный подпалиндром (подпоследовательность максимальной длины, которая является палиндромом). Пусть $d(i, j)$ - ответ на задачу для подстроки, начинающаяся с символа $i$ и заканчивающаяся в символе $j$. Ясно, что $d(i, j) = 0$ для всех $i, j,$ таких что $i > j$ и $d(i, i) = 1$ для всех $i$. Пусть нам нужно посчитать значение для $d(i, j)$, причем значение $d$ для всех $l, r$, таких что уже посчитаны и они оптимальны. Рассмотрим два случая:
- , тогда
- , тогда
Доказательство:
- Так , символы $s(i)$ и $s(j)$ не могут входить в максимальный подпалиндром одновременно, то есть либо $s(i)$ входят в максимальный подпалиндром(тогда его длина $d[i, j - 1]$), либо $s(j)$ входит в максимальный подпалиндром (тогда его длина $d[i + 1, j]$), либо оба не входят в максимальный подпалиндром (тогда его длина $= d[i, j - 1] = d[i + 1, j]$).
- Данное равенство следует из факта, что выгодно включить в максимальный подпалиндром символы $s(i)$ и $s(j)$.
Примеры задач
- Задача о расстановке знаков в выражении
- Задача о порядке перемножения матриц
- Задача о выводе в контекстно-свободной грамматике, алгоритм Кока-Янгера-Касами
- Задача об оптимальном префиксном коде с сохранением порядка. Монотонность точки разреза
- Задача о наибольшей общей подпоследовательности
- Задача о редакционном расстоянии, алгоритм Вагнера-Фишера
- Задача о расстоянии Дамерау-Левенштейна
Принцип оптимальности на подмножествах
Требуется посчитать функцию , где — некоторое множество. Принцип состоит в следующем: пусть для всех множеств (где ) известен оптимальный ответ для функции . Тогда будем вычислять через такие . В качестве примера рассмотрим задачу о коммивояжере.
Обозначим как наименьшую стоимость пути из вершины в вершину , проходящую (не считая вершины ) единожды по всем тем и только тем вершинам , для которых (т.е. уже найденный оптимальный путь от -ой вершины до -ой, проходящий через те вершины, где . Если ,то эти вершины еще не посещены). Тогда воспользуемся принципом оптимальности на подмножествах. Стоимостью минимального гамильтонова цикла в исходном графе будет значение — стоимость пути из -й вершины в -ю, при необходимости посетить все вершины.
Примеры задач
Мемоизация
| Определение: |
| Мемоизация (англ. memoization) — сохранение результатов выполнения функций для предотвращения повторных вычислений. |
Это один из способов оптимизации, применяемый для увеличения скорости выполнения компьютерных программ. Перед вызовом функции проверяется, вызывалась ли функция ранее:
- если не вызывалась, функция вызывается и результат её выполнения сохраняется;
- если вызывалась, используется сохранённый результат.
В качестве примера рассмотрим задачу о нахождении числа Фибоначчи под номером . Без мемоизации:
int Fibonacci(int n):
if n <= 1
return 1
a = Fibonacci(n - 1)
b = Fibonacci(n - 2)
return a + b
С мемоизацией:
int Fibonacci(int n):
if n <= 1
return 1
if fib[n] == -1 // проверка на то, не посчитали ли мы это число раньше; посчитанные числа хранятся в массиве fib
fib[n] = Fibonacci(n - 1) + Fibonacci(n - 2)
return fib[n]
См.также
Источники информации
- Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 15
- T. H. Cormen. «Introduction to Algorithms» third edition, Chapter 15
- Wikipedia — Optimal substructure
- Wikipedia — Greedy algorithm
- Wikipedia — Dynamic programming
- Wikipedia — Memoization
- Википедия — Жадный алгоритм
- Википедия — Динамическое программирование
- Википедия — Мемоизация
</wikitex>