Полином Жегалкина

Полином Жегалкина — полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:

[math]P = a_0 \oplus a_1 x_1 \oplus a_2 x_2 \oplus ... \oplus a_n x_n \oplus a_{n+1} x_1 x_2 \oplus ... \oplus a_{..n + C_{n}^2} x_{n-1} x_n \oplus ... \oplus a_{2^n-1} x_1 x_2 ... x_n [/math]

Предпосылки

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали

1. Хотя бы одна функция, не сохраняющая 0;
2. Хотя бы одна функция, не сохраняющая 1;
3. Хотя бы одна нелинейная функция;
4. Хотя бы одна немонотонная функция;
5. Хотя бы одна несамодвойственная функция.

Исходя из этого, система функций [math]\bigl\langle \wedge, \oplus, 1 \bigr\rangle[/math] является полной, так как в ней:

1. Не сохраняет 0: [math] 1 [/math];
2. Не сохраняет 1: [math] \oplus [/math];
3. Нелинейна: [math] \wedge [/math];
4. Немонотонна: [math] \oplus [/math];
5. Несамодвойственны: [math] \wedge, \oplus, 1 [/math].

На основе этой системы и строятся полиномы Жегалкина.

Построение полинома Жегалкина

Существует несколько способов построения полинома Жегалкина.

По таблице истинности

Пусть для функции [math]f(x_1,x_2,..,x_n)[/math] задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что [math] a \oplus 1 = \bar{a}[/math], а [math] a \oplus 0 = a[/math]. За каждую подстановку находим только один коэффициент.

Пример: Дана функция [math]f(x_1,x_2,x_3,x_4)[/math] и её таблица истинности:

[math]x_1[/math]	[math]x_2[/math]	[math]x_3[/math]	[math]x_4[/math]	[math]f(x_1,x_2,x_3,x_4)[/math]
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	0

Построим для неё полином Жегалкина:

[math]f(x_1,x_2,x_3,x_4) = a_0 \oplus a_1 x_1 \oplus a_2 x_2 \oplus a_3 x_3 \oplus a_4 x_4 \oplus a_5 x_1 x_2 \oplus a_6 x_1 x_3 \oplus a_7 x_1 x_4 \oplus a_8 x_2 x_3 \oplus a_9 x_2 x_4 \oplus a_{10} x_3 x_4 \oplus a_{11} x_1 x_2 x_3 \oplus a_{12} x_1 x_2 x_4 \oplus a_{13} x_1 x_3 x_4 \oplus a_{14} x_2 x_3 x_4 \oplus a_{15} x_1 x_2 x_3 x_4[/math]

Так как [math]f(0,0,0,0) = 0[/math], то [math]a_0 = 0[/math]. Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:

[math]f(1,0,0,0) = a_0 \oplus a_1 = 1 \Rightarrow a_1 = 1[/math]

[math]f(0,1,0,0) = a_0 \oplus a_2 = 0 \Rightarrow a_2 = 0[/math]

[math]f(0,0,1,0) = a_0 \oplus a_3 = 0 \Rightarrow a_3 = 0[/math]

[math]f(0,0,0,1) = a_0 \oplus a_4 = 0 \Rightarrow a_4 = 0[/math]

[math]f(1,1,0,0) = a_0 \oplus a_1 \oplus a_2 \oplus a_5 = 1 \Rightarrow a_5 = 0[/math]

[math]f(1,0,1,0) = a_0 \oplus a_1 \oplus a_2 \oplus a_6 = 0 \Rightarrow a_6 = 1[/math]

[math]f(1,0,0,1) = a_0 \oplus a_1 \oplus a_2 \oplus a_7 = 0 \Rightarrow a_7 = 1[/math]

[math]f(0,1,1,0) = a_0 \oplus a_2 \oplus a_3 \oplus a_8 = 1 \Rightarrow a_8 = 1[/math]

[math]f(0,1,0,1) = a_0 \oplus a_2 \oplus a_4 \oplus a_9 = 0 \Rightarrow a_9 = 0[/math]

[math]f(0,0,1,1) = a_0 \oplus a_3 \oplus a_4 \oplus a_{10} = 0 \Rightarrow a_{10} = 0[/math]

[math]f(1,1,1,0) = a_0 \oplus a_1 \oplus a_2 \oplus a_3 \oplus a_5 \oplus a_6 \oplus a_8 \oplus a_{11} = 1 \Rightarrow a_{11} = 0[/math]

[math]f(1,1,0,1) = a_0 \oplus a_1 \oplus a_2 \oplus a_4 \oplus a_5 \oplus a_7 \oplus a_9 \oplus a_{12} = 0 \Rightarrow a_{12} = 0[/math]

[math]f(1,0,1,1) = a_0 \oplus a_1 \oplus a_3 \oplus a_4 \oplus a_6 \oplus a_7 \oplus a_{10} \oplus a_{13} = 1 \Rightarrow a_{13} = 0[/math]

[math]f(0,1,1,1) = a_0 \oplus a_2 \oplus a_3 \oplus a_4 \oplus a_8 \oplus a_9 \oplus a_{10} \oplus a_{14} = 0 \Rightarrow a_{14} = 1[/math]

[math]f(1,1,1,1) = a_0 \oplus a_1 \oplus a_2 \oplus a_3 \oplus a_4 \oplus a_5 \oplus a_6 \oplus a_7 \oplus a_8 \oplus a_9 \oplus a_{10} \oplus a_{11} \oplus a_{12} \oplus a_{13} \oplus a_{14} \oplus a_{15} = 0 \Rightarrow a_{15} = 1[/math]

Таким образом, полином Жегалкина выглядит так:

[math]f(x_1,x_2,x_3,x_4) = x_1 \oplus x_1 x_3 \oplus x_1 x_4 \oplus x_2 x_3 \oplus x_2 x_3 x_4 \oplus x_1 x_2 x_3 x_4[/math]

Преобразование дизъюнктивной нормальной формы

Этот способ основан на том, что [math] X \oplus 1 = \bar{X} [/math]. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как [math] X \oplus X = 0 [/math]), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:

[math] A \lor B = AB \oplus A \oplus B [/math]   [math] (1) [/math].

Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.

Пример: Дана функция в ДНФ [math] f(x_1,x_2,x_3,x_4) = (x_1 \land x_2 \land \neg x_3 \land x_4) \lor (\neg x_1 \land \neg x_4) \lor (x_1 \land x_2) \lor x_2 [/math], построим полином Жегалкина.

Запишем функцию так:

[math]f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 + \neg x_1 \neg x_4 + x_1 x_2 + x_2[/math];

Сгруппируем слагаемые и воспользуемся преобразованием (1):

[math]f(x_1,x_2,x_3,x_4) = (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_1 x_2 \neg x_3 x_4 \neg x_1 \neg x_4) + (x_1 x_2 \oplus x_2 \oplus x_1 x_2 x_2)[/math]

Воспользуемся свойствами конъюнкции [math]A \land A = A[/math] и [math]\neg A \land A = 0[/math], а также тем, что [math]A \oplus A = 0[/math], и упростим выражение:

[math]f(x_1,x_2,x_3,x_4) = (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4) + x_2 [/math]

Ещё раз воспользуемся преобразованием (1):

[math]f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_2 \oplus (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4)x_2[/math]

Раскроем скобку по алгебраическим правилам:

[math]f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_2 \oplus x_1 x_2 x_2 \neg x_3 x_4 \oplus \neg x_1 x_2 \neg x_4 [/math]

Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:

[math]f(x_1,x_2,x_3,x_4) = \neg x_1 \neg x_4 \oplus x_2 \oplus \neg x_1 x_2 \neg x_4 [/math]

Заменим отрицание на прибавление [math]1[/math]:

[math]f(x_1,x_2,x_3,x_4) = (x_1 \oplus 1) (x_4 \oplus 1) \oplus x_2 \oplus (x_1 \oplus 1) x_2 (x_4 \oplus 1)[/math]

Раскроем скобки:

[math]f(x_1,x_2,x_3,x_4) = x_1 x_4 \oplus x_1 \oplus x_4 \oplus 1 \oplus x_2 \oplus x_1 x_2 x_4 \oplus x_1 x_2 \oplus x_2 x_4 \oplus x_2[/math]

Выкинем парные слагаемые и получим окончательную формулу:

[math]f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 \oplus x_4 \oplus 1[/math]

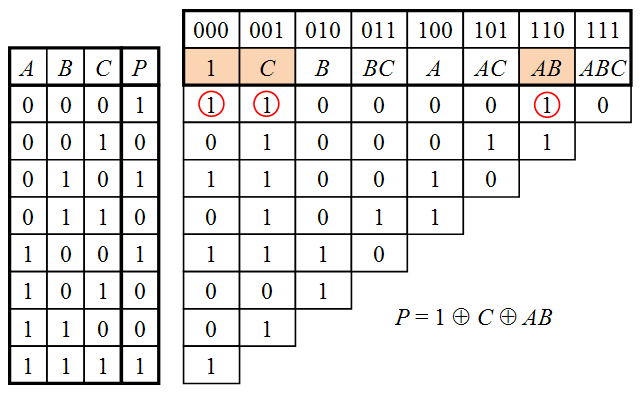
Метод треугольника

Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:

1. Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000...00 до 111...11.
2. Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
3. Ячейка в каждом последующем столбце получается путём суммирования по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
4. Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
5. Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т.д.
6. Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.

Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных P(A,B,C) показан на рисунке.

Преобразование Мёбиуса

Пусть задана булева функция [math]f: B^n \rightarrow B, \;\; B=\{ 0; 1 \}[/math]. Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.

Пусть [math] i = (i _1, i _2, .. i_n), \;\; i_k \in \{0 ; 1\}[/math], и введем обозначение [math] x ^{i_k} \sim \left\{\begin{matrix} x, \;\; i_k=1 \\ 1, \;\; i_k=0 \end{matrix}\right. [/math]  . 

Тогда полином Жегалкина можно записать как: [math] f(x) = \bigoplus\limits_i \alpha_i \cdot x_1^{i_1} \cdot x_2^{i_2} \cdot ... \cdot x_n^{i_n}[/math], где [math]\alpha_i \in \{ 0; 1 \}[/math].

Множество коэффициентов [math]\{\alpha _i\}[/math] можно рассматривать как функцию [math]\alpha[/math], заданной на множестве индексов [math] i \in \overline{1..n}[/math], то есть [math]\alpha: i \mapsto \alpha_i[/math].

Очевидно, функцию [math] f [/math] можно записать и следующим образом: [math] f(x) = \bigoplus \limits_i \alpha_i \cdot [x_1 , \; [/math] если [math] \;\; i_1] \cdot [x_2 , \; [/math] если [math] \;\; i_2] \cdot ... \cdot [x_n , \; [/math] если [math] \;\; i_n][/math].

Тут запись [math][x_k , \; [/math] если [math] \; i_k][/math] означает, что элелемент [math] x_k [/math] присутствует в соответствующем члене полинома только если [math] i_k = 1 [/math]. Тогда если для какого-то [math]x[/math], [math]i \succ x[/math] ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что [math] f(x) = \bigoplus \limits_{i \preceq x} \alpha_i [/math].   [math] (2) [/math] Найдем отображение [math] f \mapsto \alpha[/math] (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов).

Теорема:

Пусть задана функция [math] f [/math]. Тогда функцию [math] \alpha_x [/math] можно найти по формуле: [math]\alpha_x = \bigoplus \limits_{j\preceq x} f(j)[/math]  [math] (3) [/math].

Доказательство:

[math]\triangleright[/math]

Докажем при помощи индукции по количеству единиц в векторе [math] x [/math] ( иначе говоря, по сумме [math]x_1+x_2+...+x_n[/math] ) и для удобства обозначим это количество единиц(сумму) [math] wt(x) [/math]. 1) База: если [math] x = 0 [/math], то, очевидно [math] f(0) = \alpha_0 [/math] 2) Пускай теорема справедлива для всех сумм [math]wt(x) \lt k[/math]. Покажем, что в таком случае она верна и для [math]wt(x) = k[/math]. По [math] (2) [/math], а далее по предположению индукции видим: [math] f(x) = \bigoplus \limits_{i \preceq x} \alpha_i = \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] \oplus \alpha_x[/math] . Рассмотрим сумму [math] \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] [/math]. Каждый элемент [math] f(j) [/math] содержится в ней, только если [math] j \preceq x [/math], и для фиксированных [math] j, x [/math] элемент [math] f(j)[/math] встречается ровно столько раз, сколько существует [math] i [/math] , таких, что [math] j \prec i \preceq x[/math]. Несложно увидеть, что таких [math] i [/math] существует ровно [math] 2^{wt(x)-wt(j)}-1 [/math], то есть нечетное количество раз. Тогда [math] \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] = \bigoplus \limits_{j\prec x} f(j) [/math]. Но тогда [math] f(x) = \left [ \bigoplus \limits_{j\prec x} f(j) \right ] \oplus \alpha_x \Leftrightarrow f(x) \oplus \bigoplus \limits_{j\prec x} f(j) = \alpha_x \Leftrightarrow \alpha_x = \bigoplus \limits_{j\preceq x} f(j)[/math]. То есть при [math]wt(x) = k[/math] формула также выполняется, значит при любых [math] x [/math] выполняется [math]\alpha_x = \bigoplus \limits_{j\preceq x} f(j)[/math].

[math]\triangleleft[/math]

Отображение [math] f \rightarrow \alpha[/math] также называется преобразованием Мёбиуса.

Видно, что [math] (2) [/math] и [math] (3) [/math] — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию [math]f[/math]. То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией.

Литература и источники информации

• Cтатистика | Математика НГУ
• Википедия
• Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика
• Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. - 470с. — ISBN 5-94057-117-4.