Определение булевой функции
| Определение: |
| Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики, англ. Boolean function) от переменных — отображение , где — булево множество. |
Элементы булева множества и обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Элементы декартова произведения называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается , а от n переменных — . Булевы функции названы так по фамилии математика Джорджа Буля.
Основные сведения
| Определение: |
| А́рность (англ. arity) функции — количество ее аргументов. |
Каждая булева функция арности полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины . Число таких векторов равно . Поскольку на каждом векторе булева функция может принимать значение либо , либо , то количество всех n-арных булевых функций равно . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:
| Таблица истинности | |||||
|---|---|---|---|---|---|
Практически все булевы функции малых арностей ( и ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).
Нульарные функции
При количество булевых функций равно , первая из них тождественно равна , а вторая . Их называют булевыми константами — тождественный нуль и тождественная единица.
Унарные функции
При число булевых функций равно .
Таблица значений булевых функций от одной переменной:
| Функции от одной переменной | ||||
|---|---|---|---|---|
| 0 | ||||
| 1 | ||||
| Сохраняет 0 | ✓ | ✓ | ||
| Сохраняет 1 | ✓ | ✓ | ||
| Самодвойственная | ✓ | ✓ | ||
| Монотонная | ✓ | ✓ | ✓ | |
| Линейная | ✓ | ✓ | ✓ | ✓ |
Названия булевых функций от одной переменной:
| Обозначение | Название |
|---|---|
| тождественный ноль, тождественная ложь, тождественное "НЕТ" | |
| тождественная функция, логическое "ДА", "YES"(англ.) | |
| отрицание, логическое "НЕТ", "НЕ", "НИ", "NOT"(англ.), "NO"(англ.) | |
| тождественная единица, тождественная истина, тождественное "ДА", тавтология |
Бинарные функции
При число булевых функций равно .
Таблица значений булевых функций от двух переменных:
| Функции от двух переменных: | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | ||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Сохраняет 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Сохраняет 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Самодвойственная | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| Монотонная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Линейная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
Названия булевых функций от двух переменных:
| Обозначение | Другие обозначения | Название |
|---|---|---|
| тождественный ноль, тождественная ложь, тождественное "НЕТ" | ||
| И И | 2И, конъюнкция | |
| больше, инверсия прямой импликации | ||
| ДА1 | первый операнд | |
| меньше, инверсия обратной импликации | ||
| ДА2 | второй операнд | |
| сложение по модулю 2, не равно, ксор, исключающее «или» | ||
| ИЛИ ИЛИ | 2ИЛИ, дизъюнкция | |
| ИЛИ-НЕ ИЛИ-НЕ | НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса | |
| равенство, эквивалентность | ||
| НЕ2 | отрицание (негация, инверсия) второго операнда | |
| больше или равно, обратная импликация (от второго аргумента к первому) | ||
| НЕ1 | отрицание (негация, инверсия) первого операнда | |
| меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму) | ||
| И-НЕ И-НЕ | НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера | |
| тождественная единица, тождественная истина, тождественное "ДА", тавтология |
Тернарные функции
При число булевых функций равно . Некоторые из них определены в следующей таблице:
| Таблица истинности некоторых тернарных функций | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Названия булевых функций трех переменных:
| Обозначения | Другие обозначения | Названия |
|---|---|---|
| 3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса | ||
| Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией | ||
| Неравенство | ||
| 3-И-НЕ, штрих Шеффера | ||
| И И И | 3-И, минимум | |
| Равенство | ||
| Тернарное сложение по модулю 2 | ||
| И ИЛИ И ИЛИ И | переключатель по большинству, 3-ППБ, мажоритарный клапан | |
| Разряд займа при тернарном вычитании | ||
| Разряд переноса при тернарном сложении | ||
| ИЛИ ИЛИ ИЛИ | 3-ИЛИ, максимум |
Представление функции формулой
| Определение: |
| Если выбрать некоторый набор булевых функций , то с использованием выбранных функций можно записать некоторые другие булевы функции. Такая запись булевой функции называется формулой (англ. formula). |
Например, если , то функция представляется в виде
Тождественность и двойственность
| Определение: |
| Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. |
Тождественность функций f и g можно записать, например, так:
Просмотрев таблицы истинности булевых функций, легко получить такие тождества:
А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:
| (законы де Моргана) |
(дистрибутивность конъюнкции и дизъюнкции)
| Определение: |
| Функция называется двойственной (англ. duality) функции , если . |
Легко показать, что в этом равенстве и можно поменять местами, то есть функции и двойственны друг другу. Из простейших функций двойственны друг другу константы и , а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.
Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.
Суперпозиции
| Определение: |
| Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных. |
Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.
Пусть нам дан некоторый набор булевых функций . Получить новую функцию, являющеюся композицией функций из , мы можем следующими способами:
- Подстановкой одной функции в качестве некоторого аргумента для другой;
- Отождествлением аргументов функций.
Полнота системы, критерий Поста
| Определение: |
| Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества. |
| Определение: |
| Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций. |
Американский математик Эмиль Пост [1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:
- функции, сохраняющие константу и ,
- самодвойственныые функции ,
- монотонные функции ,
- линейные функции .
Набор булевых функций является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов , иными словами, когда в нем имеется хотя бы одна функция, не сохраняющая ноль, хотя бы одна функция, не сохраняющая один, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.
Представление булевых функций
Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:
- Как построить по данной функции представляющую её формулу?
- Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
- В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
- Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ)
| Определение: |
| Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов. |
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.
Примеры ДНФ:
.
.
Конъюнктивная нормальная форма (КНФ)
| Определение: |
| Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. |
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.
Пример КНФ:
Полином Жегалкина
| Определение: |
| Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. |
Полином Жегалкина имеет следующий вид:
С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: , который, в свою очередь, по теореме Поста является полным.
Примеры:
Тождественные функции. Выражение функций друг через друга
| Определение: |
| Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения. |
Приведение тождественной функции есть выражение булевой функции через другие.
Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.
| Пример: |
| Выразим следующие функции через систему функций .
|
Подстановка одной функции в другую
| Определение: |
| Подстановкой (англ. substitution) функции в функцию называется замена -того аргумента функции значением функции :
|
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.
При подстановке функции вместо -того аргумента функции , результирующая функция будет принимать аргументы, которые можно разделить на следующие блоки:
| 1. | — аргументы функции до подставленного значения функции |
| 2. | — используются как аргументы для вычисления значения функции |
| 3. | — аргументы функции после подставленного значения функции |
| Пример: |
| Исходные функции:
|
Отождествление переменных
| Определение: |
| Отождествлением переменных (англ. identification of variables) называется подстановка -того аргумента функции вместо -того аргумента:
|
Таким образом, при отождествлении переменных мы получаем функцию с количеством аргументов .
| Пример: |
| — исходная функция
— функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию — проектор единственного аргумента. |
Схемы из функциональных элементов
| Определение: |
| Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе , в котором:
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса . |
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
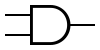
|
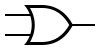
|
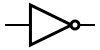
|

|
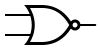
|
Стандартный базис
| Определение: |
| Стандартный базис — система булевых функций: |
Если рассматривать множество бинарных булевых функций , то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания:
Функции являются отрицаниями функций соответственно.
Тождественность функций можно доказать с помощью таблицы истинности.
Пример:
Выразим через стандартный базис обратную импликацию .
Полнота стандартного базиса
| Утверждение: |
Стандартный базис является полной системой булевых функций |
| Данное утверждение - следствие теоремы об СДНФ. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше. |
Замечание:
Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:
(конъюнктивный базис Буля)
(дизъюнктивный базис Буля)
Теоремы о числе функций в базисе
| Теорема: |
Максимально возможное число булевых функций в безызбыточном базисе — четыре. |
| Доказательство: |
|
Рассмотрим произвольный безызбыточный базис . Тогда по теореме Поста содержит следующие функции (не обязательно различные): , где — классы Поста. Значит, так как — безызбыточный базис, а система — полная, то Рассмотрим . Возможны два случая: 1. , тогда также не сохраняет единицу и немонотонная, т.е. . Значит, . 2. , тогда несамодвойственная, т.е. . Значит, . |
| Теорема: |
Для любого числа найдётся базис , что . |
| Доказательство: |
|
Приведём примеры базисов для каждого : ; ; ; ; Докажем, что последняя система является базисом: ; ; ; (доказывается с помощью таблицы истинности). |
См. также
Примечания
Источники информации
- Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. — М.: Наука, 1969.
- Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. — М.: «Энергия», 1980. — 344 с.
- Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.
- Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1986.
- Алексеев В. Б. Дискретная математика (курс лекций, II семестр). Сост. А. Д. Поспелов
- Быкова С. В., Буркатовская Ю. Б., Булевы функции, учебно-методический комплекс, Томск, 2006
- Учебные пособия кафедры математической кибернетики ВМиК МГУ
- Булева функция — Википедия
- http://psi-logic.narod.ru/bool/bool.htm