Теорема о нижней оценке для сортировки сравнениями — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(Статься переписана, добавлены источники, категории, шаблон "определение")
Строка 1: Строка 1:
−
В этой статье рассматриваются алгоритмы сортировки сравнением. В таких алгоритмах единственным действием с элементами массива является их сравнение. Значения самих элементов или иная информация о них не доступна.  
+
{{Определение
 +
|definition=Сортировка сравнениями {{---}} алгоритм сортировки, который совершает операции сравнения элементов, но никак не использует их внутреннюю структуру.
 +
}}
  
 
{{
 
{{
 
Теорема
 
Теорема
 
|about=о нижней оценке для сортировки сравнениями
 
|about=о нижней оценке для сортировки сравнениями
−
|statement=В наихудшем случае в ходе выполнения любого алгоритма сортировки сравнением выполняется <tex>\Omega(n \log n)</tex> сравнений, где <tex>n</tex> - число элементов массива.
+
|statement=В худшем случае любой алгоритм сортировки сравнениями выполняет <tex>\Omega(n \log n)</tex> сравнений, где <tex>n</tex> {{---}} число сортируемых элементов. (Теорема справедлива и для рандомизированных алгоритмов сортировки, но в статье не приводится доказательство этого факта).
  
−
|proof=Во-первых, будем считать целью нашего алгоритма определить исходную перестановку, после её определения сортировка сведется к нахождению обратной перестановки. Будем искать наихудший случай для алгоритма среди всех возможных перестановок чисел от 1 до <tex>n</tex>, таким образом у каждого сравнения всего два возможных исхода - <tex>a_i < a_j</tex> или <tex>a_i > a_j</tex>.
+
|proof=Любому алгоритму сортировки сравнениями можно сопоставить дерево. В нем узлами являются операции сравнения элементов, ребрами {{---}} переходы между состояниями алгоритма, а листьями {{---}} конечные перестановки элементов (соответствующие завершению алгоритма сортировки). Необходимо доказать, что высота такого дерева для любого алгоритма сортировки сравнениями не меньше чем <tex>O(n \log n)</tex>, где <tex>n</tex> {{---}} количество элементов.
  
−
Рассмотрим некоторое состояние нашего алгоритма. В этом состоянии уже известны результаты каких-то сравнений, и в зависимости от них делается следующее, после чего алгоритм переходит в одно из двух состояний. Кроме того, алгоритм может остановиться, если исходная перестановка будет однозначно установлена. Заметим, что этот процесс можно описать двоичным деревом, узлы которого будут соответствовать состояниям, листья - определенным входным перестановкам, а ребра - результатам сравнений.
+
При сравнении двух элементов, существует два возможных исхода (<tex>a_i < a_j</tex> и <tex>a_i \geq a_j</tex>), значит, каждый узел дерева имеет не более двух сыновей. Всего существует <tex>n!</tex> различных перестановок <tex>n</tex> элементов, значит, число листьев нашего дерева не менее <tex>n!</tex> (в противном случае некоторые перестановки были бы не достижимы из корня, а, значит, алгоритм не правильно работал бы на некоторых исходных данных).
  
−
Вот пример такого дерева для <tex>n = 3</tex>:
+
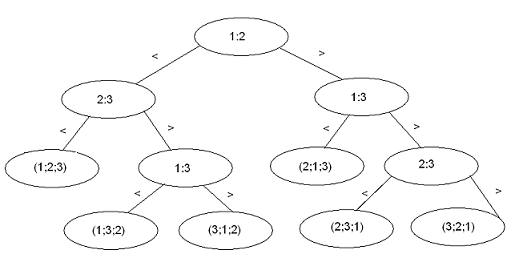
Пример дерева для алгоритма сортировки <tex>n = 3</tex> элементов:
  
 
[[Файл:DecisionTree.png]]
 
[[Файл:DecisionTree.png]]
  
−
Заметим так же, что число листьев у этого дерева должно быть не меньше <tex>n!</tex>, иначе одна из перестановок не сможет быть определена.
 
  
−
Число сравнений в наихудшем случае будет равно глубине этого дерева, поэтому осталось показать, что эта глубина есть <tex>\Omega(n \log n)</tex>. Для этого заметим, что у двоичного дерева глубины <tex>n</tex> листьев не больше <tex>2^n</tex> (в случае полного двоичного дерева), т. е. у двоичного дерева с <tex>n</tex> листьям глубина по крайней мере <tex>\lceil \log_2 n \rceil</tex>. Осталось оценить <tex>\log_2 n! = \log_2 1 + \log_2 2 + \ldots + \log_2 n ></tex><tex>n/2 \log_2 (n/2) = n/2(\log_2 n - 1)=\Omega (n \log n)</tex>
+
Докажем, что двоичное дерево с <tex>n!</tex> листьями имеет глубину <tex>\Omega(n \log n)</tex>:
  
−
Итак, для любого алгоритма сортировки сравнениями существует такая перестановка, на которой он выполнит <tex>\Omega(n \log n)</tex> сравнений, ч. т. д.
+
<tex> h = \log_2 n! = log_2 1 + \log_2 2 + \ldots + \log_2 n ></tex> <tex>n/2 \log_2 (n/2) = n/2(\log_2 n - 1) = \Omega (n \log n)</tex>
 +
 
 +
Итак, для любого алгоритма сортировки сравнениями, существует такая перестановка, на которой он выполнит <tex>\Omega(n \log n)</tex> сравнений, ч. т. д.
 
}}
 
}}
  
 
==Источники==
 
==Источники==
 
* Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с
 
* Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с
 +
* [http://da.kalinin.ru/2011/lectures/20110902-1/linear-sort.pdf Андрей Калинин Сортировка за линейное время]
 +
* [http://lectures.stargeo.ru/alg/algorithms.htm#_Toc308850829 Конспект по курсу "Алгоритмы и алгоритмические языки"] (доказательство теоремы через формулу Стирлинга).
 +
 +
[[Категория: Дискретная математика и алгоритмы]]
 +
[[Категория: Сортировки]]

Версия 21:21, 7 мая 2012

Определение:
Сортировка сравнениями — алгоритм сортировки, который совершает операции сравнения элементов, но никак не использует их внутреннюю структуру.


Теорема (о нижней оценке для сортировки сравнениями):
В худшем случае любой алгоритм сортировки сравнениями выполняет [math]\Omega(n \log n)[/math] сравнений, где [math]n[/math] — число сортируемых элементов. (Теорема справедлива и для рандомизированных алгоритмов сортировки, но в статье не приводится доказательство этого факта).
Доказательство:
[math]\triangleright[/math]

Любому алгоритму сортировки сравнениями можно сопоставить дерево. В нем узлами являются операции сравнения элементов, ребрами — переходы между состояниями алгоритма, а листьями — конечные перестановки элементов (соответствующие завершению алгоритма сортировки). Необходимо доказать, что высота такого дерева для любого алгоритма сортировки сравнениями не меньше чем [math]O(n \log n)[/math], где [math]n[/math] — количество элементов.

При сравнении двух элементов, существует два возможных исхода ([math]a_i \lt a_j[/math] и [math]a_i \geq a_j[/math]), значит, каждый узел дерева имеет не более двух сыновей. Всего существует [math]n![/math] различных перестановок [math]n[/math] элементов, значит, число листьев нашего дерева не менее [math]n![/math] (в противном случае некоторые перестановки были бы не достижимы из корня, а, значит, алгоритм не правильно работал бы на некоторых исходных данных).

Пример дерева для алгоритма сортировки [math]n = 3[/math] элементов:

DecisionTree.png


Докажем, что двоичное дерево с [math]n![/math] листьями имеет глубину [math]\Omega(n \log n)[/math]:

[math] h = \log_2 n! = log_2 1 + \log_2 2 + \ldots + \log_2 n \gt [/math] [math]n/2 \log_2 (n/2) = n/2(\log_2 n - 1) = \Omega (n \log n)[/math]

Итак, для любого алгоритма сортировки сравнениями, существует такая перестановка, на которой он выполнит [math]\Omega(n \log n)[/math] сравнений, ч. т. д.
[math]\triangleleft[/math]

Источники

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Теорема_о_нижней_оценке_для_сортировки_сравнениями&oldid=22002»