Теорема о нижней оценке для сортировки сравнениями
Сортировка сравнениями (англ. Comparison sort) — алгоритм сортировки, который совершает операции сравнения элементов, но никак не использует их внутреннюю структуру.
| Теорема (о нижней оценке для сортировки сравнениями): |
В худшем случае любой алгоритм сортировки сравнениями выполняет сравнений, где — число сортируемых элементов. |
| Доказательство: |
|
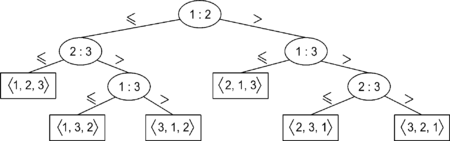
Любому алгоритму сортировки сравнениями можно сопоставить дерево. В нем узлам соответствуют операции сравнения элементов, ребрам — переходы между состояниями алгоритма, а листьям — конечные перестановки элементов (соответствующие завершению алгоритма сортировки). Необходимо доказать, что высота такого дерева для любого алгоритма сортировки сравнениями не меньше чем , где — количество элементов. Ограничимся рассмотрением сортировки перестановок элементов. При сравнении некоторых двух из них, существует два возможных исхода ( и ), значит, каждый узел дерева имеет не более двух сыновей. Всего существует различных перестановок элементов, значит, число листьев нашего дерева не менее (в противном случае некоторые перестановки были бы не достижимы из корня, а, значит, алгоритм не правильно работал бы на некоторых исходных данных).
Докажем, что двоичное дерево с не менее чем листьями имеет глубину . Легко показать, что двоичное дерево высоты имеет не более чем листьев. Значит, имеем неравенство , где — число листьев. Прологарифмировав его, получим: Итак, для любого алгоритма сортировки сравнениями, существует такая перестановка, на которой он выполнит сравнений. |
Следствия
| Утверждение: |
Пирамидальная сортировка и сортировка слиянием являются асимптотически оптимальными сортировками сравнением. |
| Верхние границы времени работы пирамидальной сортировки и сортировки слиянием совпадают с нижней границей для наихудшего случая из теоремы о нижней границе для сортировки сравнениями. |
| Утверждение: |
Любая сортирующая сеть с $n$ нитями имеет размер $\Omega(n \log n)$. |
|
Каждый компаратор реализует одно сравнение двух элементов. Поэтому сортирующая сеть является алгоритмом сортировки, который основан на сравнениях, при чем количества компараторов и сравнений в этом алгоритме совпадают. Значит, их $\Omega(n \log n)$ |
| Утверждение: |
Любая сортирующая сеть с $n$ нитями имеет глубину $\Omega(\log n)$. |
|
На каждом слое может быть не более $\dfrac{n}{2}$ компараторов, так как внутри одного слоя гнезда компаратора крепятся к разным нитям, а их $n$. Пусть $d$ — количество слоев этой сети. Тогда количество компараторов $k \leqslant \dfrac{n}{2} \cdot d$ Теорема утверждает, что количество сравнений этого алгоритма (то есть количество компараторов) $k = \Omega(n\log n)$. Это означает, что найдется такая константа $c$, что $k \geqslant c \cdot n \log n$. Таким образом $c \cdot n \log n \leqslant k \leqslant \dfrac{n}{2} \cdot d \Rightarrow c \cdot n \log n \leqslant \dfrac{n}{2}\cdot d \Rightarrow 2c\log n \leqslant d \Rightarrow d = \Omega(\log n)$ |
| Утверждение: |
Не существует алгоритма добавления элемента в упорядоченный массив с сохранением порядка, за истинное время $\mathcal{o}(\log n)$, где $n$ — количество элементов в массиве, |
|
Допустим, есть такой алгоритм. Тогда создадим пустой массив и будем последовательно добавлять в него элементы массива, который хотим отсортировать. В итоге на выходе алгоритма получим отсортированный массив. Тогда сравнений будет $\mathcal{o}(\log 1 + \log 2 + \ldots + \log{(n-1)}) = \mathcal{o}(n\log n)$. Но теорема утверждает, что их должно быть $\Omega(n\log n)$. |
| Утверждение: |
Не существует структуры данных, которая одновременно поддерживает добавление элементов и извлечение минимума за амортизированное время . |
|
Если бы такая структура существовала, то с её помощью можно было бы отсортировать все элементы за амортизированное время — добавить все элементы, а затем извлечь минимальный раз. Можно заметить, что теореме даётся оценка на истинную нижнюю границу, а в данном утверждении фигурирует амортизированное время. Но этот факт не является проблемой, так как амортизированное время на одну операцию в случае операций даст суммарное истинное время . |
См. также
Источники информации
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с
- Андрей Калинин Сортировка за линейное время
- Конспект по курсу "Алгоритмы и алгоритмические языки" (доказательство теоремы через формулу Стирлинга).
- Лекториум "Алгоритмы сортировки"