Сортирующие сети — различия между версиями
Darkraven (обсуждение | вклад) |
Darkraven (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
}} | }} | ||
[[Image:Sorting-network-comparator-demonstration..png|thumb|130px|Сортирующая сеть с 2 проводами]] | [[Image:Sorting-network-comparator-demonstration..png|thumb|130px|Сортирующая сеть с 2 проводами]] | ||
| − | |||
| − | |||
| Строка 38: | Строка 36: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Сеть компараторов является сортирующей тогда и только тогда, когда она сортирует | + | Сеть компараторов с <tex>n</tex> входами является сортирующей тогда и только тогда, когда она сортирует <tex>2^n</tex> различных последовательностей из 0 и 1. |
}} | }} | ||
{{main | 0-1 принцип}} | {{main | 0-1 принцип}} | ||
Версия 14:41, 30 мая 2012
Содержание
Определение
| Определение: |
| Сеть называется сортирующей (Sorting network), если в результате её работы любая последовательность входных данных преобразуется в монотонно неубывающую. |
Компараторы (сравнивающие устройства)
| Определение: |
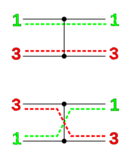
| Компаратор (Comparator) — устройство, подключенное к двум проводам, которое упорядочивает текущие значения на проводах. |
Обычно компараторы меньшее значение передают на провод с меньшим номером, но бывают и направленные компараторы, у которых указано направление перемещения.
| Определение: |
| K-компаратор — устройство, упорядочивающее значения на k проводах. |
Компараторы можно располагать в одном слое, если они подключены к разным проводам. В этом случае сравнения будут выполняться параллельно.
Сравнивающие сети
| Определение: |
| Сравнивающая сеть — несколько компараторов, соединенных проводами. Используется для упорядочивания числовых последовательностей. |
| Определение: |
| Глубина сети (depth) — количество слоев в сети. |
| Определение: |
| Размер сети (size) — количество компараторов в сети. |
| Теорема: |
Сеть компараторов с входами является сортирующей тогда и только тогда, когда она сортирует различных последовательностей из 0 и 1. |
См.также
Сортирующие сети для квадратичных сортировок
Источники
- Кормен Глава 28 Сортирующее сети.
- Wikipedia - Sorting networks