Простейшие методы синтеза схем из функциональных элементов

Определение:

Синтезом схемы из функциональных элементов называется процедура получения логической схемы, реализующей заданную логическую функцию.

Приведем несколько простейших алгоритмов синтеза схем, реализующих произвольную функцию от [math] n [/math] аргументов [math] f(x_{1}, ..., x_{n}) [/math], в случае когда базис [math] B = \{\neg, \lor, \land\} [/math].

Метод синтеза, основанный на совершенной ДНФ

Лемма (1):

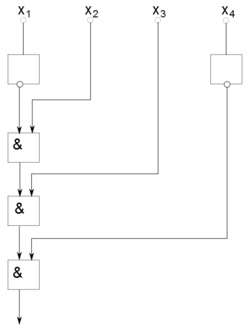
Для любой функции [math] f(x_{1}, ..., x_{n}) [/math], реализующей конъюнкцию [math] n [/math] аргументов, [math] size_{B}(f)\le 2n-1 [/math]

Доказательство:

[math]\triangleright[/math]

Рис. 1 Построим данную схему следующим образом: возьмем [math] n [/math] элементов отрицания, присоединенных к выходам, и цепочки из элементов конъюнкции, имеющих [math] n [/math] "свободных" входов. Каждый [math] i [/math]-й вход этой цепочки присоединяется к входу схемы, если [math] i [/math]-й множитель равен [math] x_{i} [/math], или к выходу [math] i [/math]-го элемента отрицания, если [math] i [/math]-й множитель равен [math] \overline{x}_{i} [/math].(рис. 1) Очевидно, что сложность построенной схемы равна [math] 2n-1 [/math]. Поэтому [math] size_{B}(f)\le 2n-1 [/math]. Лемма доказана.

[math]\triangleleft[/math]

Теорема (1):

Для любой функции [math] f(x_{1}, ..., x_{n}) [/math] имеет место неравенство [math] size_{B}(f)\le n2^{n+1} [/math]

Доказательство:

[math]\triangleright[/math]

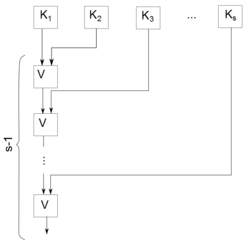
Рис. 2 Пусть [math] f(x_{1},...,x_{n}) [/math] --- произвольная булева функция. Если [math] f \ne 0 [/math], то [math] f [/math] может быть задана нормальной дизъюнктивной формой [math] f(x_{1},...,x_{n}) = K_{1} \vee K_{2} \vee ... \vee K_{s} [/math], где [math] s \le 2^{n} [/math] и каждая конъюнкция имеет вид [math] K_{j}=x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{i} [/math] Схема [math] S [/math] для [math] f [/math] состоит из конъюнкций [math] K_{j} [/math] (каждая из них в соответствии с Леммой 1 имеет сложность не более [math] 2n-1 [/math]) и цепочки из [math] s-1 [/math] элемента дизъюнкции с [math] s [/math] свободными входами. Свободные входы этой цепочки присоединяются к выходам схем для конъюнкций [math] K_{j} [/math].(рис. 2) Имеем [math] size_{B}(f)\le s\cdot(2n-1)+s-1 \lt s\cdot(2n-1)+s = 2ns \le n2^{n+1} [/math]. Если [math] f = 0 [/math], то схема строится в соответствии с представлением [math] 0=x_{1}\wedge\overline{x}_{1} [/math], то есть[math] size_{B}(0) \le 2[/math]. Таким образом, для любой функции [math] f(x_{1},...,x_{n}) [/math] выполняется неравенство [math] size_{B}(f(x_{1},...,x_{n}))\le n2^{n+1} [/math]. Поэтому [math] size_{B}(f)\le n2^{n+1} [/math]. Теорема доказана.

[math]\triangleleft[/math]

Метод синтеза, основанный на более компактной реализации множества всех конъюнкций

Определение:

[math] f(n) \sim g(n) [/math] означает, что [math]f[/math] асимптотически эквивалентна [math]g[/math], то есть [math]\lim_{n \to \infty}\frac{f(n)}{g(n)} = 1[/math]

Определение:

[math] f(n) \lesssim g(n) [/math] означает, что [math]\overline{\lim}_{n \to \infty}\frac{f(n)}{g(n)} \le 1[/math]

Лемма (2):

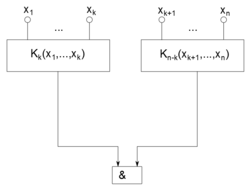
Для функции [math] K_{n} [/math], реализующей конъюнкцию [math] n [/math] элементов, имеет место соотношение [math] size_{B}(K_{n}) \sim 2^n [/math]

Доказательство:

[math]\triangleright[/math]

Рис. 3 Разделим цепочки конъюнкций на две части. Каждая конъюнкция [math] x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{i} [/math] может быть представлена в виде конъюнкции двух конъюнкций длины [math] k [/math] и [math] n-k [/math]: [math] x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{n} = (x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{k})(x_{k+1}\wedge\overline{x}_{k+2}\wedge{x}_{k+3}\wedge ... \wedge{x}_{n}) [/math]. Поэтому схема для [math] K_{n} [/math] может быть образована из схем для [math] K_{k}(x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{n}) [/math] и [math] K_{n-k}(x_{k+1}\wedge\overline{x}_{k+2}\wedge{x}_{k+3}\wedge ... \wedge{x}_{n}) [/math] и системы из [math] 2^n [/math] элементов конъюнкции, осуществляющих вышеприведенную операцию.(рис. 3) Следовательно, [math] size_{B}(K_{n}) \le size_{B}(K_{k}) + size_{B}(K_{n-k}) + 2^n [/math]. Так как по Теореме 1 [math] size_{B}(K_{n}) \le k2^{k+1} [/math] , [math] size_{B}(K_{n-k}) \le (n-k)2^{n-k+1} [/math],то [math] size_{B}(K_{n}) \le k2^{k+1} + (n-k)2^{n-k+1} + 2^n [/math]. Положим [math] k=[\frac{n}{2}][/math]. Тогда [math] k \le \frac{n}{2} [/math], [math] n-k \le \frac{n}{2}+1 [/math] и [math] size_{B}(K_{n}) \le \frac{n}{2}2^{\frac{n}{2}+1} + (\frac{n}{2}+1)\frac{n}{2}2^{\frac{n}{2}+2} + 2^n =2^n+O(n2^{\frac{n}{2}})[/math]. С другой стороны, при [math] n \ge 2 [/math] каждая конъюнкция реализуется на выходе некоторого элемента, то есть при [math] n \ge 2 [/math] выполняется неравенство [math] size_{B}(K_{n}) \ge 2^{n} [/math]. Таким образом, [math] size_{B}(K_{n}) \sim 2^n [/math]. Лемма доказана.

[math]\triangleleft[/math]

Теорема (2):

Для любой функции [math] f(x_{1}, ..., x_{n}) [/math] имеет место соотношение [math] size_{B}(f)\lesssim 2^{n+1} [/math].

Доказательство:

[math]\triangleright[/math]

Пусть [math] f(x_{1},...,x_{n}) [/math] произвольная булева функция,[math] f \ne 0 [/math]. Заменим в схеме (рис. 2) верхнюю часть схемы, реализующую конъюнкции [math] K_{1} \vee K_{2} \vee ... \vee K_{s} [/math], схемой, реализующей все конъюнкции из [math] K_{n} [/math]. Тогда для любой такой функции [math] f(x_{1},...,x_{n}) [/math] (не равной нулю) имеем [math] size_{B}(f) \le size_{B}(K_{n})+s-1 \le size_{B}(K_{n})+2^{n}-1 \lesssim 2^{n+1} [/math] Таким образом, [math] size_{B}(f)\lesssim 2^{n+1}. [/math] Теорема доказана.

[math]\triangleleft[/math]

Метод синтеза схем К.Э.Шеннона

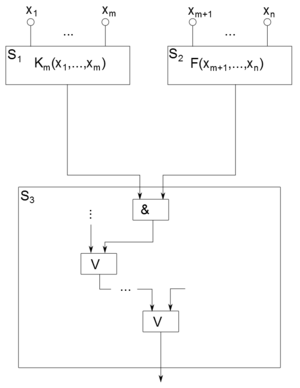
Теорема (3):

Для любой функции [math] f(x_{1}, ..., x_{n}) [/math] имеет место соотношение [math] size_{B}(f)\lesssim 12\frac {2^{n}}{n} [/math].

Доказательство:

[math]\triangleright[/math]

Рис. 4 Пусть [math] f(x_{1},...,x_{n}) [/math] произвольная булева функция. Рассмотрим разложение [math] f [/math] по переменным [math] x_{1},...,x_{n} [/math], где [math] 1 \le m \le n [/math]: [math] f(x_{1},...,x_{n})= \bigvee x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{m} f(x_{m+1}\wedge\overline{x}_{m+2}\wedge{x}_{m+3}\wedge ... \wedge{x}_{n}) [/math]. Схема для функции [math] f [/math] строится из трех подсхем: [math] S_{1},S_{2},S_{3} [/math]. (рис. 4) 1. Схема [math] S_{1} [/math] реализует все конъюнкции из множества [math] K_{m} (x_{1},...,x_{m}) [/math]. В силу Леммы 2 выполняется неравенство [math] size_{B}(S_{1}) \le size_{B}(K_{m}) \lesssim 2^{m} [/math]. 2. Схема [math] S_{2} [/math] реализует систему [math] F(x_{m+1},...,x_{n}) [/math] всех булевых функций от переменных [math] x_{m+1},...,x_{n} [/math]. Другими словами, подсхема [math] S_{2} [/math] вычисляет все булевы функции, зависящие от последних [math] n - m [/math] переменных. В силу Теоремы 1 [math] size_{B}(S_{2}) \le (n-m)2^{n-m+1}2^{2^{n-m}} [/math]. 3. Схема [math] S_{3} [/math] производит "сборку" в соответствии с разложением функции [math] f [/math]: для каждого набора реализуется конъюнкция [math] x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{m}f(x_{m+1}\wedge\overline{x}_{m+2}\wedge{x}_{m+3}\wedge ... \wedge{x}_{n}) [/math] ([math] 2^{m} [/math] элементов конъюнкции) и образуется дизъюнкция таких конъюнкций ([math] 2^{m}-1 [/math] элементов дизъюнкции). Поэтому выполняется неравенство [math] size_{B}(S_{3}) \le 2^{m} +2^{m} -1 [/math]. Таким образом, [math] size_{B}(f) \le size_{B}(S_{1})+size_{B}(S_{2})+size_{B}(S_{3}) \lesssim 3 \cdot 2^{m} +(n-m)2^{n-m+1}2^{2^{n-m}} [/math]. Положим (для упрощения дальнейших выкладок) [math] k=n-m [/math]. Тогда [math] size_{B}(f) \lesssim 3 \cdot 2^{n-k} +k2^{k+1}2^{2^{k}} [/math]. Заметим, что второе слагаемое "очень быстро" растет с ростом [math] k [/math], а первое слагаемое убывает с ростом [math] k [/math] медленней. Поэтому следует взять такое значение [math] k [/math], при котором первое и второе слагаемые приблизительно равны, и потом немного уменьшить [math] k [/math]. Тогда второе слагаемое "сильно" уменьшится, а первое "не очень сильно" возрастет. Возьмем, например, [math] k=\log_{2}n [/math]. Тогда [math] 3 \cdot 2^{n-k} = 3 \cdot \frac{2^{n}}{n} [/math], [math] k \cdot 2^{k+1} \cdot 2^{2^{k}}=\log_{2}n\cdot (2n)\cdot 2^{\frac{n}{2}}[/math], то есть получили "слишком много". Возьмем [math] k [/math] на единицу меньше: [math] k=\log_{2}n-1 [/math]. Тогда [math] 3 \cdot 2^{n-k} = 3 \cdot \frac{2^{n}}{n} \cdot 2 [/math], [math] k \cdot 2^{k+1} \cdot 2^{2^{k}}=(\log_{2}n-1)\cdot n\cdot 2^{\frac{n}{2}}[/math]. Вспомним теперь, что [math] k [/math] должно быть целым числом, и положим [math] k=[\log_{2}n-1] [/math]. Тогда [math] n-k \lt n- \log_{2} + 2[/math], [math] 3 \cdot 2^{n-k} \lt 12 \cdot \frac {2^{n}}{n} [/math], [math] k\cdot 2^{k+1}\cdot 2^{2^{k}} \le (\log_{2}-1)\cdot n\cdot 2^{\frac{n}{2}} [/math]. При этом выборе [math] k [/math] окончательно имеем [math] size_{B}(n)\lesssim 12\frac {2^{n}}{2} [/math]. Теорема доказана.

[math]\triangleleft[/math]

Литература

• Яблонский С.В. Введение в дискретную математику. — 4-е изд. — М.: Высшая школа, 2003. — 384 с. — ISBN 5-06-004681-8