Квадродеревья — различия между версиями
Gromak (обсуждение | вклад) |
Gromak (обсуждение | вклад) |
||
| Строка 45: | Строка 45: | ||
Если совсем кратко, то запрос выглядит так: | Если совсем кратко, то запрос выглядит так: | ||
<code> | <code> | ||
| + | QTree-RangeSearch(P, M): | ||
if (P is a leaf) then | if (P is a leaf) then | ||
if (P.point in M) then | if (P.point in M) then | ||
| Строка 54: | Строка 55: | ||
[https://groups.google.com/forum/#!topic/uw.cs.cs240/MGfrsvKAiMA Тут] говорят, что работает за <tex>\theta (d + n)</tex>. Видимо, так и есть, но я пока не понял, как это обосновать, может показаться, что <tex>\theta (d \cdot n)</tex>. | [https://groups.google.com/forum/#!topic/uw.cs.cs240/MGfrsvKAiMA Тут] говорят, что работает за <tex>\theta (d + n)</tex>. Видимо, так и есть, но я пока не понял, как это обосновать, может показаться, что <tex>\theta (d \cdot n)</tex>. | ||
| + | Ну а вообще, можно делать по-тупому за <tex>O(n)</tex>, но, видимо, так обычно быстрее получается. | ||
| + | |||
| + | == Сбалансированное квадродерево == | ||
| + | Квадродерево называется '''сбалансированным''', если для соответствующего ему разбиения плоскости на квадраты верно, что для любых двух соседних квадратов их стороны отличаются не более чем в два раза. | ||
| + | |||
| + | Тут можно ещё что-то написать, но вроде это не нужно, поэтому оставлю только определение. | ||
| + | |||
| + | == Сжатое квадродерево == | ||
| + | Обычное квадродерево может иметь слишком большую глубину независимо от количества точек. Сжатое дерево лишено данного недостатка, имеет глубину <tex>O(n)</tex>, и на его основе строится [[Skip quadtree: определение, время работы | Skip Quadtree]]. | ||
| + | |||
| + | Назовём квадрат интересным, если соответствующая ему вершина дерева имеет хотя бы 2 непустых ребёнка (то есть таких, что в их квадратах содержится хотя бы одна точка) или является корнем. Понятно, что любой квадрат <tex>p</tex>, содержащий хотя бы две точки, содержит единственный наибольший интересный квадрат. | ||
| − | |||
== Литература == | == Литература == | ||
| − | * ''van Kreveld, de Berg, Overmars, Cheong {{---}} Computational Geometry. Algorithms and Applications.'' Страница 309. | + | * ''van Kreveld, de Berg, Overmars, Cheong {{---}} Computational Geometry. Algorithms and Applications.'' Страница 309. Тут можно почитать про квадродеревья. |
| + | * [http://arxiv.org/pdf/cs.cg/0507049.pdf Статья на архиве про Skip Quadtree] Тут можно почитать про сжатое квадродерево. | ||
| + | * [http://en.wikipedia.org/wiki/Quadtree Квадродерево на Википедии] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D0%BD%D1%82%D0%BE%D0%B2 Даже на русский переведено, оказывается] | ||
Версия 13:06, 6 января 2014
Содержание
Определение и построение
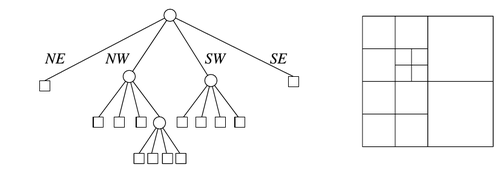
Квадродерево — дерево, каждая внутренняя вершина которого содержит 4 ребёнка. Любому узлу квадродерева соответствует некоторый квадрат. Если внутренней вершине соответствует какой-то квадрат , то её детям соответствуют четверти квадрата (см. картинку).
Вообще говоря, квадродеревья могут быть использованы для разных целей и хранить разные данные, но нам они нужны для перечисления точек в произвольном прямоугольнике, соответственно, хранить в них будем какой-то набор точек.
Пусть дано множество точек , для которого нужно построить квадродерево. Начнём с некоторого квадрата , содержащего все точки из . Если он не дан явно, его можно легко найти за линейное время от числа вершин. Пусть . Обозначим . Тогда:
- если содержит не больше одной точки, то квадродерево состоит из одного листа, которому соответствует квадрат ;
- иначе корнем дерева делаем вершину , которой соответствует квадрат , а его дети — , и им соответствуют квадраты , , , . Затем таким же образом рекурсивно превращаем каждого ребёнка в квадродерево для множества точек, лежащих в соответствующем квадрате.
Леммы и теоремы
Сперва оценим глубину квадродерева. Если какие-то две точки лежат очень близко, то процесс построения может продолжаться очень долго, поэтому глубину невозможно оценить функцией от числа вершин.
| Лемма: |
Глубина квадродерева для множества точек не превосходит , где — наименьшее расстояние между двумя точками из , а — сторона квадрата, с которого начинается построение квадродерева. |
| Доказательство: |
| Сторона квадрата на глубине , очевидно, равна . Максимальное расстояние между двумя точками внутри квадрата достигается, когда они являются вершинами диагонали, то есть на глубине расстояние между любыми двумя точками в одном квадрате не превосходит . Поскольку внутренняя вершина квадродерева содержит хотя бы 2 точки в соответствующем ей квадрате, то , так как — минимальное расстояние между точками в . Отсюда следует, что . Значит, глубина любой внутренней вершины не превосходит , из чего следует утверждение леммы. |
Размер дерева и время построения будут также зависеть и от — мощности .
| Теорема: |
Квадродерево глубины для точек содержит вершин и может быть построено за . |
| Доказательство: |
|
Поскольку каждая внутренняя вершина имеет четырёх детей, то суммарное число листьев будет , где — число внутренних вершин. Поэтому достаточно доказать оценки лишь для внутренних вершин. Каждая внутренняя вершина содержит хотя бы одну точку в соответствующем ей квадрате. Заметим, что квадраты с одного уровня не пересекаются и полностью покрывают весь исходный квадрат (в котором точек). Значит, число внутренних вершин одного уровня не может первосходить . Из этого следует, что всего внутренних вершин . При построении квадродерева наиболее длительная операция на каждом шаге — распределение точек по четвертям текущего квадрата. Таким образом, время, затрачиваемое на одну внутренню вершину, линейно зависит от числа точек в соответствующем ей квадрате. Как отмечалось выше, на одном уровне суммарно во всех внутренних вершинах не больше точек, из чего следует доказываемая оценка. |
Перечисление точек в произвольном прямоугольнике
Пусть на вход подаётся некоторый прямоугольник , для которого надо вернуть все точки из множества , которые принадлежат этому прямоугольнику.
Алгоритм следующий:
- если мы лист, то просто проверяем, лежит ли наша точка в , и возвращаем её, если да;
- иначе запускаемся от детей и возвращаем объединение всего того, что вернули дети.
Псевдокод можно посмотреть здесь. Там немного по-другому (хранят не больше 4-х точек в каждой вершине дерева, а у нас подразумевается, что точки явно хранятся только в листьях), но в целом почти такой же.
Если совсем кратко, то запрос выглядит так:
QTree-RangeSearch(P, M):
if (P is a leaf) then
if (P.point in M) then
report P.point
for each child C of P do
if C.region intersects M then
QTree-RangeSearch(C, M)
Тут говорят, что работает за . Видимо, так и есть, но я пока не понял, как это обосновать, может показаться, что . Ну а вообще, можно делать по-тупому за , но, видимо, так обычно быстрее получается.
Сбалансированное квадродерево
Квадродерево называется сбалансированным, если для соответствующего ему разбиения плоскости на квадраты верно, что для любых двух соседних квадратов их стороны отличаются не более чем в два раза.
Тут можно ещё что-то написать, но вроде это не нужно, поэтому оставлю только определение.
Сжатое квадродерево
Обычное квадродерево может иметь слишком большую глубину независимо от количества точек. Сжатое дерево лишено данного недостатка, имеет глубину , и на его основе строится Skip Quadtree.
Назовём квадрат интересным, если соответствующая ему вершина дерева имеет хотя бы 2 непустых ребёнка (то есть таких, что в их квадратах содержится хотя бы одна точка) или является корнем. Понятно, что любой квадрат , содержащий хотя бы две точки, содержит единственный наибольший интересный квадрат.
Литература
- van Kreveld, de Berg, Overmars, Cheong — Computational Geometry. Algorithms and Applications. Страница 309. Тут можно почитать про квадродеревья.
- Статья на архиве про Skip Quadtree Тут можно почитать про сжатое квадродерево.
- Квадродерево на Википедии
- Даже на русский переведено, оказывается