Skip quadtree: определение, время работы
Описание
Skip quadtree — структура данных, напоминающая skip-list, которая позволяет эффективно локализоваться и производить операции над множеством точек.
В данной статье будет рассматриваться только рандомизированая версия этой структуры.
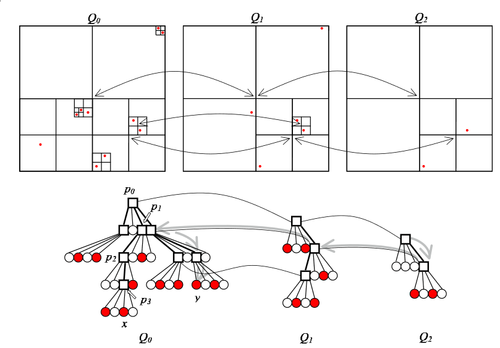
The randomized skip quadtree — последовательность сжатых квадродеревьев над последовательностью подмножеств некоторого исходного множества точек . , в каждый элемент из входит с вероятностью , то есть . The randomized skip quadtree состоит из последовательности , где — сжатое квадродерево над множеством . Будем называть эти квадродеревья уровнями, при этом нулевой уровень содержит в точности точки из .
На рисунке представлено дерево, состоящее из трех слоев: , , . Одинаковые вершины, находящиеся на разных уровнях, соединены линиями. Стрелками обозначены переходы в процессе локализации при поиске точки .
Любая вершина однозначно определяется своими координатами на каждом уровне. Поэтому по вершине с уровня мы можем получить ее на уровне , если она интересная на уровне , так как в противном случае она могла быть сжата.
Заметим, что если какой-то квадрат интересный в , то он интересный и в , так как по определению структуры.
Операции над skip quadtree
Для реализации операций нам нужно уметь получать по вершине с уровня соответствующую ей вершину с уровня . Сделать это можно двумя способами:
- Хранить в вершине ссылку на вершину уровнем ниже.
- Так как каждая вершина однозначно задается своими координатами, можем сопоставить ей маску. Используем ассоциативный массив, чтобы по маске получать ссылку на вершину. Такие массивы будем хранить для каждого уровня skip quadtree.
Локализация
Локализация выполняется аналогично локализации в сжатом квадродереве. Под локализацией подразумевается, что мы хотим найти минимальный интересный квадрат, геометрически содержащий данную точку. Сначала локализуемся в квадродереве наибольшего уровня, начиная с его корня. Затем локализуемся в квадродереве уровнем ниже, начиная уже не с корня, а с того квадрата, который нашли на прошлом уровне. Но на каждом уровне, кроме нулевого, локализумся не до листа, а до глубочайшего интересного. Продолжаем, пока не дойдём до нулевого уровня.
Вставка
При вставке сначала локализуемся сразу на всех уровнях, запоминая ссылки, дальше добавляем вершину на нулевой уровень, затем с вероятностью добавляемся на уровень выше и так далее до первого недобавления. При этом количество уровней может увеличиться максимум на , то есть, если появился новый уровень, то процесс заканчивается.
Удаление
При удалении локализуемся и удаляем вершину со всех уровней, на которых она есть, не забывая обновлять ссылки или ассоциативный массив. При этом какой-то уровень мог стать пустым, в таком случае выкинем его.
Время работы и память
| Лемма (О количестве шагов на одном уровне): |
На каждом уровне в среднем совершается шагов поиска для любой точки . |
| Доказательство: |
|
Пусть в (то есть на -ом уровне) поиск точки , начинающийся с корня, проходит по квадратам . Пусть случайная величина — количество шагов поиска в , тогда — последний квадрат из , являющийся интересным в . Оценим вероятность того, что делается шагов. Забьём на случай , так как он не важен при расчёте мат. ожидания. На пути будет хотя бы непустых четвертинок. У первого квадрата на этом пути есть хотя бы 2 непустые четвертинки, одна из них — следующий квадрат на пути, в котором тоже хотя бы 2 непустые четвертинки, и так далее. В последнем квадрате просто хотя бы 2 непустые четвертинки. Чтобы был последним из интересным квадратом в небходимо, чтобы среди этих как минимум непустых четвертинок только одна (вероятность этого назовём ) или ноль (вероятность этого назовём ) были непустыми в . Иначе, если будет хотя бы пара непустых четвертинок, то их наименьший общий предок в дереве будет интересным квадратом и будет находиться глубже . Таким образом, искомая вероятность не превосходит .
, потому что это в сущности вероятность того, что ни одна точка из как минимум непустых четвертинок не попала на уровень выше. , потому что это в сущности вероятность того, что ровно одна точка из как минимум непустых четвертинок попала на уровень выше.
|
| Лемма (О количестве уровней): |
Математическое ожидание количества уровней составляет |
| Доказательство: |
|
Для оценки мат. ожидания посчитаем вероятность того, что количество уровней равно . . , потому что вероятность того, что точка дойдёт до уровня , равна . , потому что вероятность того, что точка не дойдёт до уровня , равна .
Теперь посчитаем мат. ожидание количества уровней:
Оценим первую сумму: , поскольку сумма этих вероятностей не превосходит единицу. Оценим вторую сумму:
Рассмотрим эту сумму:
Суммируя всё вышесказанное, получаем, что . Для лучшего понимания можно представлять, что . |
| Теорема (О времени работы): |
Поиск, добавление и удаление точки работают за в среднем. |
| Доказательство: |
| Напрямую следует из двух предыдущих лемм. |
| Теорема (О занимаемой памяти): |
Математическое ожидание занимаемой памяти — . |
| Доказательство: |
| Сжатое квадродерево для точек занимает памяти. На нулевом уровне точек. На следующем уровне точек, дальше и так далее. Получим геометрическую прогрессию, в итоге памяти. |
Запрос точек в прямоугольнике
Задача: нам дается прямоугольник, нужно выдать все точки, лежащие в нем.
Реализация запроса на сжатом квадродереве занимает времени. Используем skip quadtree для ускорения поиска. Для этого ослабим условие задачи, тогда skip quadtree позволит очень быстро (асимптотически) отвечать на такие запросы.
Ослабление: расширим данный прямоугольник на . Тогда в ответ могут попасть точки не из данного прямоугольника, но лежащие внутри -области. В большинстве практических задач данное ослабление не ухудшит конечный результат, а только ускорит процесс.
Skip quadtree позволяет отвечать на запрос всех точек, лежащих в прямоугольнике, окруженном -областью, за , где — число точек в ответе. Алгоритм можно модифицировать для ответа на запрос точек в любой выпуклой фигуре.
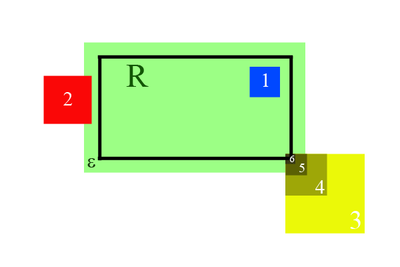
Обозначим наш прямоугольник . Тогда -область — область , охватывающая , граница которой удалена от его сторон на .
Данный прямоугольник разбивает вершины на следующие классы:
- — внутренние, то есть лежащие внутри -области (1 и 6 на рисунке).
- — внешние, то есть лежащие вне прямоугольника (2 на рисунке).
- — пронзающие, пересекающие , но не являющиеся внутренними (3, 4 и 5 на рисунке).
Для вершин из классов и ответ на запрос находится тривиально — все поддерево вершины и никакие точки из поддерева соответственно; сложность представляют вершины из класса . Зная их все, мы можем ответить на запрос.
Мощность множества пронзающих вершин может составлять , так как пронзающие вершины могут быть вложены друг в друга, тогда как нам достаточно рассмотреть только наименьшую из вложенных вершин.
Назовем пронзающую вершину критической, если для каждого из ее детей выполняется одно из двух условий:
- ребенок не является пронзающей вершиной.
- ребенок является пронзающим, но содержит меньшую часть , чем рассматриваемая вершина.
На рисунке среди вершин 3, 4, 5, 6 только 5 является критической.
Вместо поиска всех пронзающих вершин, для решения задачи достаточно найти все критические вершины.
| Лемма (Об упаковке): |
Количество критических вершин на нулевом уровне дерева равно . |
| Доказательство: |
|
Для квадратов с длиной стороны верно, что они либо , либо , то есть вершин с такой стороной не бывает, как и со стороной меньше . Все точки, содержащиеся в skip quadtree, находятся внутри какого-то прямоугольника, значит, длина его стороны — константа. Поэтому длина стороны области пересечения запрашиваемого прямоугольника со skip quadtree — это тоже константа. Тогда длина стороны запрашиваемого прямоугольника — . Пронзающих вершин c длиной стороны чуть больше , области которых не пересекаются, может быть — длина стороны прямоугольника, деленная на . Тогда всего их может быть , так как пронзающие вершины могут быть вложенными, и длина стороны родителя в два раза больше, чем у ребенка, то количество родителей вершин с такой стороной в два раза меньше. Критических вершин не больше, чем пронзающих, так что их тоже . |
Алгоритм
Начинаем отвечать на запрос с корня и определяем тип вершин.
- Если вершина внутренняя, добавляем ее в ответ вместе с поддеревом.
- Если внешняя, то игнорируем.
- Если критическая, то рассмотрим всех ее детей.
- Если не критическая, то найдем минимальную критическую, содержащую ту же часть , что и рассматриваемая вершина.
Первые три варианта рассматриваются тривиально. Покажем, как для данной некритической вершины найти минимальную критическую вершину , содержащую ту же часть , что и . Для это найдем такое , что будет критической вершиной в при максимальном . И будем действовать аналогично процессу локализации.
Таким образом, поиск займет времени. А так как критических вершин всего , то итоговая ассимптотика составит .
Псевдокод
void points_in_rectangle(rectangle R, rectangle E, vector<point>& points)
queue<node> que
que.push(.root)
while (!que.empty())
node n = que.pop()
rectangle K // прямоугольник, соответсвующий вершине n
if (R K == )
continue
else if (n is leaf)
if (n.point in R)
points.push_back(n.point)
else if (K E)
n.add_subtree(points) // добавляем все точки поддерева внутренней вершины
else if (n is not critical)
node q // некритическая вершина на максимальном уровне, соответствующая n
level = k - 1 // максимальный уровень, на котором вершина q некритическая
// k - количество уровней в skip quadtree
while (level > 0)
node = n from // вершина, соответствующая n в дереве
if ( != null and is not critical)
q =
break
level--
while (true)
if (q is not critical)
node qc = ребенок q, содержащий ту же область E, что и q
if (qc is not leaf or level == 0)
q = qc
else if (level > 0)
level--
q = q from
else if (level != 0)
level--
q = q from
else
break
que.push(q)
else
que.add_all(n.children)