Алгоритм Колусси — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Псевдокод)
Строка 120: Строка 120:
 
       '''while''' k <= m
 
       '''while''' k <= m
 
         '''while''' x[i] == x[i - k]
 
         '''while''' x[i] == x[i - k]
−
             i++;
+
             i++
 
         hmax[k] = i
 
         hmax[k] = i
 
         '''int''' q = k + 1
 
         '''int''' q = k + 1
Строка 127: Строка 127:
 
             q++
 
             q++
 
         k = q
 
         k = q
−
         if k == i + 1
+
         '''if''' k == i + 1
 
             i = k
 
             i = k
 
       '''return''' hmax
 
       '''return''' hmax

Версия 22:57, 14 июня 2014

Алгоритм, разработанный Ливио Колусси, профессором итальянского университета Padova, и опубликованный им в 1991 году, является продолжением работы над оптимизацией алгоритма Кнута-Морриса-Пратта. Предназначен для поиска одной подстроки в одном тексте.

Алгоритм

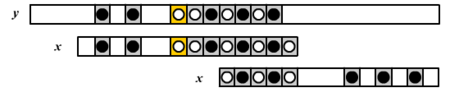
Алгоритм сравнивает символы шаблона [math]x[/math] один за другим с символами исходной строки [math]y[/math]. Для сдвигов шаблона относительно исходной строки применяются вспомогательные функции, описанные ниже.

Пусть [math]|y|=n[/math] и [math]|x|=m[/math].

Обозначим за [math]\mathrm{Kmp}[/math] — префикс-функцию, но при этом она определена для [math]x[0] \dots x[m-1][/math] и имеет значение [math]-1[/math] по умолчанию.

Отметим, что нумерация символов строк и элементов массива у нас начинается с [math]0[/math].

Множество всех позиций шаблона разделим на два дизъюнктных множества. Тогда каждая попытка сравнения шаблона с исходной строкой после очередного сдвига состоит из двух случаев.


Определение:
В первом случае сравнения выполняются слева направо с символами текста, выровненными с шаблоном в позиции, для которой значение функции [math]\mathrm{Kmp}(i)[/math] строго больше [math]-1[/math]. Такие позиции будем называть насыщенными (англ. noholes).


Определение:
Во втором случае будут производиться сравнения в оставшихся позициях справа налево. Такие позиции будем называть ненасыщенными (англ. holes).


Такая стратегия предоставляет, как минимум, 2 преимущества:

  • когда несовпадение появляется во время первого случая, после соответствующего сдвига уже нет необходимости делать проверки в насыщенных позициях, которые были проверены на предыдущем шаге.
  • когда несовпадение появляется во время второго случая, это означает, что суффикс шаблона совпал с подстрокой исходной строки [math]y[/math] и после соответствующего сдвига префикс шаблона будет все ещё совпадать с этой подстрокой, поэтому нет необходимости в повторной проверке.


Определение:
Обозначим за [math]\mathrm{K_{min}}(i) = \min\{k : \ x[0 \dots i-1-k]=x[d \dots i-1]\ and\ x[i-k] \neq x[i]\}[/math]. Функция [math]\mathrm{K_{min}}[/math] определена для всех позиций [math]i[/math], у которых [math]\mathrm{Kmp}(i) \neq -1[/math].


Если [math]\mathrm{K_{min}}(i) \neq 0[/math], то периодичность шаблона [math]x[/math] заканчивается в позиции [math]i[/math].

Очевидно, что для [math]0 \lt i \lt m[/math] позиция [math]i[/math]:

  • насыщенная, если [math]\mathrm{K_{min}}(i-1) \neq 0[/math],
  • ненасыщенная, в остальных случаях.

Обозначим за [math]nd+1[/math] количество насыщенных позиций в шаблоне [math]x[/math].

Массив [math]h[/math] содержит первыми элементами [math]nd+1[/math] насыщенных позиций в возрастающем порядке и затем [math]m-nd-1[/math] ненасыщенных в убывающем порядке, т.е.

  • для всех [math]0 \leqslant i \leqslant nd[/math] [math]h[i][/math] насыщенная позиция и [math]h[i] \lt h[i+1][/math] для [math]0 \leqslant i \lt nd[/math].
  • для всех [math]nd \lt i \lt m[/math] [math]h[i][/math] ненасыщенная и [math]h[i] \gt h[i+1][/math] для [math]nd \lt i \lt m-1[/math].


Определение:
Обозначим за [math]\mathrm{R_{min}}(i)[/math] наименьший период [math]r[/math] шаблона [math]x[/math] большего, чем [math]i[/math]. Функция [math]\mathrm{R_{min}}[/math] определена для всех позиций [math]i[/math], у которых [math]\mathrm{Kmp}(i) = -1[/math].


Определение:
Обозначим за [math]\mathrm{first}(u)[/math] наименьшее число [math]v[/math] такое, что [math]u \leqslant h[v][/math].


Теперь рассмотрим 2 случая, возможных при очередной попытке сравнения шаблона с подстрокой из текста. Допустим, что шаблон [math]x[/math] выровнен с подстрокой [math]y[j \dots j+m-1][/math].

Первый случай

Рассмотрим случай, когда [math]x[h[k]]=y[j+h[k]][/math] для [math]0 \leqslant k \lt r \lt nd[/math] и [math]x[h[r]] \neq y[j+h[r]][/math].

Пусть [math]j' = j + \mathrm{K_{min}}(h[r])[/math].

Тогда нет вхождений шаблона [math]x[/math], начиная с [math]y[j \dots j'][/math] и [math]x[/math] может быть сдвинут на [math]\mathrm{K_{min}}(h[r])[/math] позиций вправо.

Кроме того равенство [math]x[h[k]]=y[j’+h[k]][/math] для всех [math]k : 0 \leqslant k \lt \mathrm{first}(h[r]-\mathrm{K_{min}}(h[r]))[/math] означает, что сравнения могут продолжены с символов [math]x[h[\mathrm{first}(h[r] - \mathrm{K_{min}}(h[r]))]][/math] и [math]y[j'+h[\mathrm{first}(h[r]-\mathrm{K_{min}}(h[r]))]][/math].

Несовпадение в насыщенной позиции. Насыщенные позиции обозначены черными кругами и сравниваются слева направо.

Второй случай

Теперь рассмотрим ситуацию, когда [math]x[h[k]]=y[j+h[k]][/math] для [math]0 \leqslant k \lt r[/math] и [math]x[h[r]] \neq y[j+h[r]][/math] для [math]nd \leqslant r \lt m[/math].

Пусть [math]j' = j + \mathrm{R_{min}}(h[r])[/math].

Тогда нет вхождений шаблона [math]x[/math], начиная с [math]y[j \dots j'][/math] и [math]x[/math] может быть сдвинут на [math]\mathrm{R_{min}}(h[r])[/math] позиций вправо.

Кроме того равенство [math]x[0 \dots m-1-\mathrm{R_{min}}(h[r])]=y[j' \dots j+m-1][/math] означает, что сравнения могут продолжены с символов [math]x[h[\mathrm{first}(m-1-\mathrm{R_{min}}(h[r]))]][/math] и [math]y[j'+h[\mathrm{first}(m-1-\mathrm{R_{min}}(h[r]))]][/math].

Несовпадение в ненасыщенной позиции. Ненасыщенные позиции обозначены белыми кругами и сравниваются справа налево.

Предварительные вычисления

Для вычисления значений [math]\mathrm{K_{min}}[/math] будем использовать вспомогательную функцию [math]\mathrm{H_{max}}[/math].

Определение:
Обозначим за [math]\mathrm{H_{max}}[/math] функцию, для которой выполняется:
  • [math]x[k \dots \mathrm{H_{max}}(k)-1]=x[0 \dots \mathrm{H_{max}}(k)-k-1][/math],
  • [math]x[\mathrm{H_{max}}(k)] \neq x[\mathrm{H_{max}}(k)-k][/math].


Определение:
Обозначим за [math]\mathrm{nhd0}(i)[/math] количество насыщенных позиций строго меньших [math]i[/math].


Теперь мы можем определить два функции [math]shift[/math] и [math]next[/math]:

  • [math]\mathrm{shift}(i)=\mathrm{K_{min}}(h[i])[/math] и [math]\mathrm{next}(i)=\mathrm{nhd0}(h[i]-\mathrm{K_{min}}(h[i]))[/math] для всех [math]i : i \lt nd[/math];
  • [math]\mathrm{shift}(i)=\mathrm{R_{min}}(h[i])[/math] и [math]\mathrm{next}(i)=\mathrm{nhd0}(m-\mathrm{R_{min}}(h[i]))[/math] для всех [math]i : nd \leqslant i \lt m[/math];
  • [math]\mathrm{shift}(m)=\mathrm{R_{min}}(0)[/math] и [math]\mathrm{next}(m)=\mathrm{nhd0}(m-\mathrm{R_{min}}(h[m-1]))[/math].

Таким образом, при возникновении несовпадения между [math]x[h[r]][/math] и [math]y[j+h[r]][/math] окно сравнения должно быть сдвинуто на [math]\mathrm{shift}(r)[/math] и сравнения могут быть продолжены с позиции [math]h[\mathrm{next}(r)][/math] шаблона [math]x[/math].

Псевдокод

Функция для построения массива [math]\mathrm{H_{max}}[/math].

Наивный вариант 

  int[] buildHmax(char[] x, int m):
     int hmax[m + 1]
     for k = 1 .. m
        int i = k
        while x[i] == x[i - k]
           i++
        hmax[k] = i
     return hmax

Явная реализация по определению, очевидно, работает за [math]O(m^2)[/math] и требует [math]O(m)[/math] памяти.

Улучшенный вариант 

  int[] buildHmax(char[] x, int m):
     int hmax[m + 1]
     int i = 1
     int k = 1
     while k <= m
        while x[i] == x[i - k]
           i++
        hmax[k] = i
        int q = k + 1
        while hmax[q - k] + k < i
           hmax[q] = hmax[q - k] + k
           q++
        k = q
        if k == i + 1
           i = k
     return hmax

На каждой итерации цикла увеличивается либо переменная [math]i[/math], либо [math]k[/math] (или переменная [math]q[/math], которая используется в конечном счете для обновления [math]k[/math]). Поскольку [math]i = 1[/math] и [math]k = 1[/math] в начале и [math]i \lt k = m + 1[/math] в конце алгоритма, количество итераций алгоритма не превосходит [math]2 \cdot m[/math]. Следовательно функция требует [math]O(m)[/math] времени и памяти.

Функция для построения массива [math]\mathrm{K_{min}}[/math]. 

  int[] buildKmin(int[] hmax, int m):
     int kmin[m]
     for i = m .. 1
        if hmax[i] < m
           kmin[hmax[i]] = i
     return kmin

Функция для построения массива [math]\mathrm{R_{min}}[/math]. 

  int[] buildRmin(int[] hmax, int[] kmin, int m):
     int rmin[m]
     int r = 0
     for i = m - 1 .. 0
        if hmax[i + 1] == m
           // [math]r[/math] — первое число большее, чем [math]i[/math] и такое, что шаблон имеет период [math]r[/math]
           r = i + 1
        if kmin[i] == 0
           rmin[i] = r
        else
           rmin[i] = 0
     return rmin

Функция для построение массива [math]\mathrm{shift}[/math]. 

  int[] buildShift(int[] kmin, int[] rmin, int[] h, int nd, int m):
     int shift[m + 1]
     for i = 0 .. nd
        shift[i] = kmin[h[i]]
     for i = nd + 1 .. m - 1
        shift[i] = rmin[h[i]]
     shift[m] = rmin[0]
     return shift

Функция для построения массива [math]\mathrm{next}[/math]. 

  int[] buildNext(int[] kmin, int[] rmin, int[] h, int nd, int m):
     // Вычисление массива [math]\mathrm{nhd0}[/math]
     int nhd0[m]
     int s = 0
     for i = 0 .. m - 1
        nhd0[i] = s
        if kmin[i] > 0
           ++s
     
     // Вычисление массива [math]\mathrm{next}[/math]
     int next[m + 1]
     for i = 0 .. nd
        next[i] = nhd0[h[i] - kmin[h[i]]]
     for i = nd + 1 .. m - 1
           next[i] = nhd0[m - rmin[h[i]]]
     next[m] = nhd0[m - rmin[h[m - 1]]]
     return next

Основная функция алгоритма Колусси. 

  function colussi(char[] x, char[] y):
     int n = length(y)
     int m = length(x) 
     
     // Предварительные вычисления
     int[] hmax = buildHmax(x, m)
     int[] kmin = buildKmin(hmax, m)
     int[] rmin = buildRmin(hmax, kmin, m)
     
     // Построение массива [math]h[/math]
     int h[m]
     int s = -1
     int r = m
     for i = 0 .. m - 1
        if kmin[i] == 0
           h[--r] = i
        else
           h[++s] = i
     int nd = s
     
     int[] shift = buildShift(kmin, rmin, h, nd, m)
     int[] next = buildNext(kmin, rmin, h, nd, m)
     
     // Поиск подстроки
     int i = 0
     int j = 0
     int last = -1
     while j <= n - m
        while i < m and last < j + h[i] and x[h[i]] == y[j + h[i]]
           ++i
        if i >= m or last >= j + h[i]
           OUTPUT(j)
           i = m
        if i > nd
           last = j + m - 1
        j += shift[i]
        i = next[i]

Асимптотики

  • Фаза предварительных вычислений занимает [math]O(m)[/math] времени и памяти;
  • В худшем случае поиск требует [math]O(n)[/math] сравнений.

где [math]n[/math] — длина исходного текста, [math]m[/math] — длина шаблона

Сравнение с другими алгоритмами

Достоинства

  • Поиск выполняется за [math]O(n)[/math] в отличие от алгоритма Кнута-Морриса-Пратта, поиск в котором занимается [math]O(n+m)[/math], что помогает уменьшить константу при [math]m \sim n[/math].
  • Фаза предобработки выполняется за [math]O(m)[/math] в отличие от алгоритма Бойера-Мура, где в наилучшем случае можно получить время [math]O(n+|\Sigma|)[/math], что плохо при больших алфавитах.

Недостатки

  • Сложность реализации.

Источники информации

  • COLUSSI L., 1991, Correctness and efficiency of the pattern matching algorithms, Information and Computation 95(2):225-251.
  • Colussi algorithm
  • Colussi.ppt
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Алгоритм_Колусси&oldid=39229»