Формула включения-исключения

Формула включения-исключения

Определение:

Формула включения-исключения (англ. Inclusion-exclusion principle) — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений.

Случай для двух множеств

Для случая из двух множеств [math] A, B [/math] формула включения-исключения имеет следующий вид:

[math] | A \cup B | = | A | + | B | - | A \cap B |[/math]

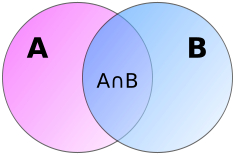
В силу того, что в сумме [math] | A | + | B |[/math] элементы пересечения [math] A \cap B [/math] учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.

Для случая с большим количеством рассматриваемых множеств [math] n [/math] процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.

Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.

Теорема:

Пусть [math] A = \bigcup \limits_{i=1}^{n}A_i [/math] , тогда по формуле включения-исключения: [math] | A | = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| [/math] Причем [math] N = \{ 1,2, \ldots ,n \} [/math]. Здесь за [math] 2^N [/math] обозначим множество всех непустых подмножеств [math] N [/math].

Доказательство:

[math]\triangleright[/math]

Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент [math] x \in \bigcup \limits_{i=1}^{n}A_i [/math]. Пусть [math] x \in \bigcap \limits_{j=1}^{t}A_{i_j} [/math]. Тогда найдем число вхождений элемента [math] x [/math] в правую часть формулы. [math]k = (-1) ^ {t + 1} {t \choose t} + (-1) ^ {t} {t \choose {t - 1}} + \ldots + (-1)^2 {t \choose 1} + (-1) {t \choose 0} = -\sum \limits_{j = 1}^{t} (-1)^j {t \choose j} [/math][math] = {t \choose 0} - \sum \limits_{j = 0}^{t} (-1)^j {t \choose j} [/math] Докажем, что [math] \sum \limits_{j = 0}^{t} (-1)^j {t \choose j} = 0[/math] В силу того, что [math] (1 + (-1)) ^ t = {t \choose 0} 1^t (-1)^0 + {t \choose 1} 1 ^ {t - 1} (-1) ^ 1 + \ldots + {t \choose t} 1^0 (-1)^t = \sum \limits_{j = 0}^{t} (-1)^j {t \choose j}[/math], имеем [math] 0 = (1 + (-1)) ^ t = \sum \limits_{j = 0}^{t} (-1)^j {t \choose j}[/math], то равенство доказано. Таким образом, [math] k = {t \choose 0} - \sum \limits_{j = 0}^{t} (-1)^j = 1 - 0 = 1[/math], то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть [math]~l[/math] — это количество множеств, мощность пересечения которых мы ищем. Для случая [math]~l=1[/math] равенство обращается в тривиальное ([math] |A| = |A_1| [/math] — истинно). Для случая [math]~l=2[/math] справедливость теоремы пояснена выше. Таким образом, [math]~l=2[/math] — база индукции. Предположим, что для [math]~l=n-1[/math] равенство верно. Докажем, что равенство истинно для [math]~l=n[/math] Пусть [math] A [/math] — объединение [math]~n[/math] множеств. Очевидно, что [math] A = \bigcup \limits_{i=1}^{n}A_i = \left( {\bigcup \limits_{i=1}^{n-1}A_i} \right) \cup A_n [/math]. Пусть [math] B = \bigcup \limits_{i=1}^{n-1}A_i [/math]; [math]N' = \{ 1,2, \ldots ,n-1 \} [/math]. Исходя из предположения индукции, имеем, что [math] | B | = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| [/math] Кроме того, так как формула верна для [math]~l=2[/math] (из базы индукции), то верно равенство [math] | A | = | B | + | A_n | - | B \cap A_n | (*)[/math]. Найдем [math]~| B \cap A_n |[/math]: Очевидно, что [math] B \cap A_n = \left( \bigcup \limits_{i=1}^{n-1}A_i \right) \cap A_n = \bigcup \limits_{i=1}^{n-1} \left( A_i \cap A_n \right) (**)[/math] Опираясь на предположение индукции и равенство [math] (**) [/math] имеем, что [math] |B \cap A_n| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} \left( A_j \cap A_n \right) \right| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| [/math] Подставим полученные значения в [math](*)[/math]: [math] | A | = | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| \right) - \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right)[/math] [math] =| A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) [/math] Докажем, что [math] | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) [/math] [math] = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| [/math] Равенство справедливо, потому что все наборы [math] I \in 2^N [/math] можно разбить на две группы : [math] I \in 2^{N'} [/math] Это означает, что в наборе точно не будет присутствовать индекс [math] n [/math], а будут все различные варианты индексов остальных множеств, т.е. [math] I \in 2^{N'}[/math]. [math]\{n\} \cup I[/math], где [math]I \in N'[/math] Аналогично предыдущему, только в наборе будет индекс [math] n [/math]. Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и [math]|A| = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| [/math] . Таким образом, для [math]~l=n[/math] мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана.

[math]\triangleleft[/math]

Беспорядки

Определение:

Беспорядок (англ. Derangement) — это перестановка чисел от [math]1[/math] до [math]n[/math], в которой ни один элемент не стоит на своём месте.

Теорема:

Количество беспорядков порядка [math]n[/math] равно субфакториалу числа [math]n[/math] (обозначение: [math]!n[/math]) и вычисляется по формуле: [math] равно !n = n! - \frac{n!}{1!} + \frac{n!}{2!} - \frac{n!}{3!} + ... + (-1)^{n}\frac{n!}{n!} = \sum_{k=0}^n(-1)^{k}\frac{n!}{k!} [/math]

Доказательство:

[math]\triangleright[/math]

Воспользуемся принципом включения-исключения: обозначим за [math]A_i[/math] — количество перестановок из [math]n[/math] элементов, в каждой из которых [math]i[/math]-ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: [math] \Big |\bigcap_{i=_1}^n \overline{A}_i \Big| = |U|-\sum \limits_{i} |A_i|+\sum \limits_{i \lt j} |A_i\bigcap A_j|-\sum \limits_{i \lt j \lt k} |A_i\bigcap A_j\bigcap A_k|[/math] [math]+ ... +(-1)^{n}| A_1 \bigcap A_2 \bigcap ... \bigcap A_n | [/math], где универсум [math]U[/math] — множество из всех перестановок порядка [math]n[/math]. [math]\overline{A}_i[/math] — количество перестановок, в каждой из которых [math]i[/math]-ый элемент стоит не на своём [math]i[/math]-ом месте. Таким образом [math]| \bigcap_{i=_1}^n \overline {A}_i |[/math] — количество всех перестановок, в каждой из которых [math]i[/math]-ый элемент [math]\neq[/math] [math]i[/math],то есть количество искомых беспорядков. [math]|A_i| = (n - 1)![/math], так как [math]i[/math]-ая позиция занята числом [math]i[/math]. [math]\binom{n}{1}[/math] — количество способов выбрать одну [math]i[/math]-ую позицию [math] \Rightarrow \sum \limits_{i = 1}^{n} |A_i| = \binom{n}{1} (n-1)![/math] Рассмотрим [math] |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| [/math], где [math] 1\leqslant i_1 \lt i_2 \lt ... \lt i_k \leqslant n [/math]. Так как некоторые [math]k[/math] позиций [math]i_1, i_2, ... , i_k [/math] заняты соответствующими числами, то количество способов расставить остальные [math]n-k[/math] чисел равно [math](n-k)![/math]. То есть [math] |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| = (n - k)! [/math] Количество всех способов выбрать [math]k[/math] позиций [math]i_1, i_2, ... , i_k [/math] равно [math]\binom{n}{k} [/math]. Таким образом получаем, что: [math]\sum \limits_{1\leqslant i_1 \lt i_2 \lt ... \lt i_k \leqslant n}^{} |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| = \binom{n}{k} \cdot(n-k)! [/math] Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем: [math]| \bigcap_{i=_1}^n \overline{A}_i | = n! + \sum \limits_{k = 1}^{n} (-1)^{k}\binom{n}{k} \cdot (n - k)!.[/math] Раскрывая [math]\binom{n}{k}[/math] по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка [math]n[/math].

[math]\triangleleft[/math]

Рекурсивная формула нахождения количества беспорядков

Утверждение:

Количество беспорядков удовлетворяет рекурсивным соотношениям: [math] d(n)=(n-1)[d(n-1)+d(n-2)] [/math] и [math] d(n)=n \times d(n-1)+(-1)^{n} [/math], где [math] d(1)=0 [/math], а [math] d(2)=1 [/math]

[math]\triangleright[/math]

1) Сначала докажем второе соотношение: Так как [math] d(n)=!n [/math], то можно переписать эту формулу, как [math] !n=n!(n-1)+(-1)^{n} [/math] По формуле субфакториала [math] !n=n!(\sum \limits_{k = 0}^{n-1} \frac {(-1)^{k}}{k!} + \frac {(-1)^{n}}{n!})=n!\sum \limits_{k = 0}^{n-1} \frac {(-1)^{k}}{k!}+(-1)^{n}=n \times !(n-1)+(-1)^{n}[/math] 2) Теперь, используя вторую формулу, докажем первую: Так же, как и первом случае, напишем формулу через субфакториал: [math] !n=(n-1)[!(n-1)+!(n-2)] [/math] Заметим, что если умножить [math] n [/math] на [math] !(n-1) [/math], то получим часть второй формулы: [math] !n=n \times !(n-1)-!(n-1)+(n-1) \ times !(n-2) [/math] Распишем субфакториалы от [math] n-2 [/math] и [math] n-1 [/math]: [math] (n-1) \times (n-2)!(\sum \limits_{k = 0}^{n-2}) \frac {(-1)^{k}}{k!}-(n-1)!(\sum \limits_{k = 0}^{n-1}) \frac {(-1)^{k}}{k!}=(-1)^{n} [/math] [math] (n-1)!(\sum \limits_{k = 0}^{n-2}) \frac {(-1)^{k}}{k!}-(n-1)!((\sum \limits_{k = 0}^{n-2}) \frac {-1)^{k}}{k!}+ \frac {(-1)^{n-1}}{(n-1)!}=(-1)^{n} [/math] Субфакториалы от [math] n-2 [/math] сокращаются, остается верное равенство [math] -(-1)^{n-1}=(-1)^{n} [/math]

[math]\triangleleft[/math]

См. также

• Производящая функция
• Лемма Бёрнсайда и Теорема Пойа

Источники информации

• Википедия — Беспорядок
• Wikipedia — Derangement
• Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, Изд. 4-е, исправленное - МЦНМО, 2013 ISBN 978-5-4439-0052-0
• Р. Стенли, Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108.