Формула включения-исключения
Содержание
Формула включения-исключения
| Определение: |
| Формула включения-исключения (англ. Inclusion-exclusion principle) — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений. |
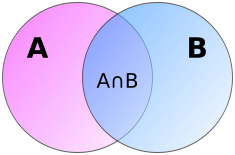
Для случая из двух множеств формула включения-исключения имеет следующий вид:
В силу того, что в сумме элементы пересечения учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.
Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.
Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.
| Теорема: |
Пусть , тогда по формуле включения-исключения: |
| Доказательство: |
|
Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент . Пусть . Тогда найдем число вхождений элемента в правую часть формулы.
Докажем, что В силу того, что , имеем , то равенство доказано. Таким образом, , то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное ( — истинно). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
Равенство справедливо, потому что все наборы можно разбить на две группы :
Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |
Беспорядки
| Определение: |
| Беспорядок (англ. Derangement) — это перестановка чисел от до , в которой ни один элемент не стоит на своём месте. |
Явная формула с использованием принципа включения-исключения
| Теорема: |
Количество беспорядков порядка равно субфакториалу [1] числа (обозначение: ) и вычисляется по формуле:
|
| Доказательство: |
|
Воспользуемся принципом включения-исключения: обозначим за — количество перестановок из элементов, в каждой из которых -ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: , где универсум — множество из всех перестановок порядка . — количество перестановок, в каждой из которых -ый элемент стоит не на своём -ом месте. Таким образом — количество всех перестановок, в каждой из которых -ый элемент ,то есть количество искомых беспорядков. , так как -ая позиция занята числом . — количество способов выбрать одну -ую позицию Рассмотрим , где . Так как некоторые позиций заняты соответствующими числами, то количество способов расставить остальные чисел равно . То есть Количество всех способов выбрать позиций равно . Таким образом получаем, что:
Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем: Раскрывая по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка . |
Рекурретное соотношение для нахождения количества беспорядков
| Утверждение: |
Количество беспорядков удовлетворяет рекурсивным соотношениям:
и , где , а |
|
1) Докажем второе соотношение: Так как , то можно переписать эту формулу, как По формуле субфакториала 2) Докажем первое соотношение: У нас есть чисел и столько же мест. Мы должны найти количество способов разместить эти числа так, что ни одно из чисел не оказалось на месте с таким же номером. Предположим, что первое число оказалось на месте с номером . Это можно сделать способами, так как первое число может оказаться на любом месте, кроме первого. Теперь есть 2 варианта, зависящие от того, окажется ли число с номером на первом месте или нет.
Эти 2 случая не пересекаются и поэтому суммируются. В первом случае число занимает первое место, затем идет распределение остальных чисел, не зависящее от первого и -го чисел. Во втором же случае число с номером попасть на первое место не может, а значит займет какое-то другое место, и распределение остальных чисел уже будет другое. В итоге получается необходимая формула. |
Задача о перестановках
Сколько есть перестановок чисел от до таких, что первый элемент больше , а последний меньше ?
Посчитаем количество "плохих" перестановок, то есть таких, у которых первый элемент (множество таких перестановок обозначим ) и/или последний (множество таких перестановок обозначим ).
Тогда количество "плохих" перестановок по формуле включений-исключений равно:
Проведя несложные комбинаторные вычисления, получим:
Отнимая это число от общего числа перестановок , получим ответ.
Задача о нахождении числа взаимно простых четвёрок
Дано чисел: . Необходимо посчитать количество способов выбрать из них четыре числа так, что они будут взаимно простыми, то есть их НОД равен единице.
Посчитаем число "плохих" четвёрок, то есть таких, в которых все числа делятся на число .
Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на (но, возможно, делящихся и на больший делитель).
,
где — это количество простых в факторизации числа , — количество четвёрок, делящихся на .
Чтобы посчитать функцию , надо просто посчитать количество чисел, кратных , и с помощью биномиальных коэффициентов посчитать число способов выбрать из них четвёрку.
Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.
См. также
Примечания
Источники информации
- Википедия — Беспорядок
- Wikipedia — Derangement
- Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, Изд. 4-е, исправленное - МЦНМО, 2013 ISBN 978-5-4439-0052-0
- Р. Стенли, Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108.