Сортирующие сети для квадратичных сортировок

Рассмотрим модели сортирующих сетей для квадратичных сортировок.

Сортирующие сети с последовательной сортировкой

На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок.

Сортировка пузырьком	Сортировка вставками	Сортировка выбором

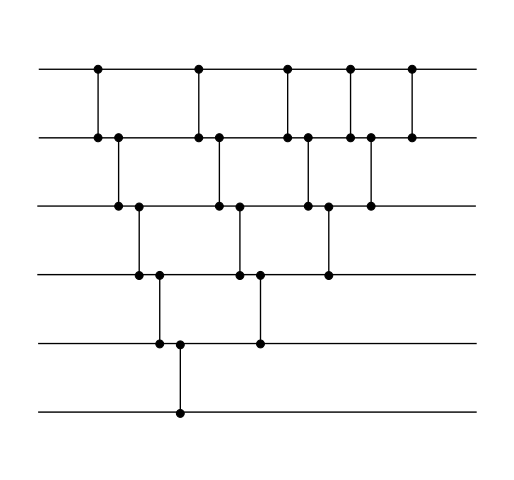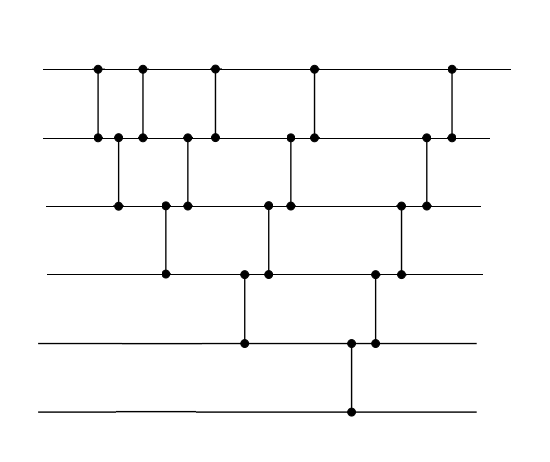Сортирующие сети с параллельной сортировкой

На один слой будем устанавливать несколько компараторов.

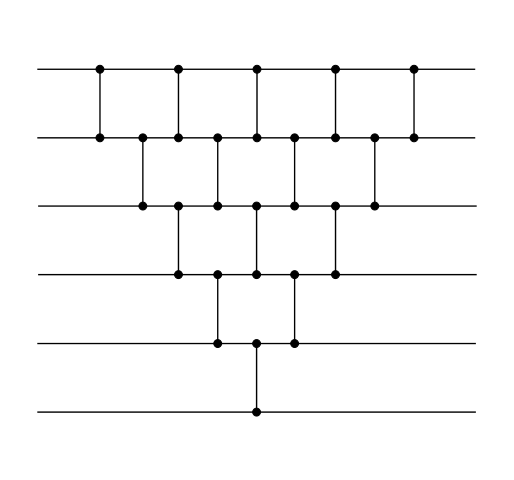
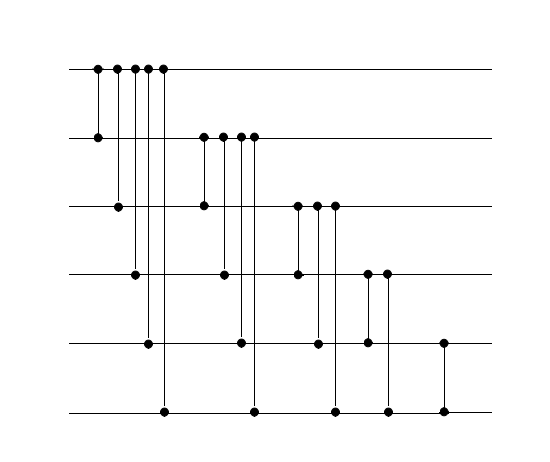
Сортировка пузырьком и вставками

• Если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же.

Теорема:

В результирующей сети будет [math](2n - 3)[/math] слоев.

Доказательство:

[math]\triangleright[/math]

Докажем данное утверждение по принципу математической индукции. Базой индукции будет [math] n = 2 [/math]. Пусть [math] S(n) = 2n - 3 [/math] - количество слоев в сети сортировки размера n. Шаг индукции: При построении [math](n + 1)[/math]-й сортирующей сети, выносим сортирующую сеть, содержащую [math]n[/math] компараторов и добавляем к ней компараторы: [math][n + 1; n], [n; n - 1]\dots[3; 2], [2; 1] [/math]. Подсчитаем количество компараторов: [math] S(n + 1) = n + n - 1 = 2n - 1 [/math] , заметим, что данное количество слоев удовлетворяет нашему шагу индукции [math](S(n + 1) = 2(n + 1) - 3 = 2n + 2 - 3 = 2n - 1)[/math]

[math]\triangleleft[/math]

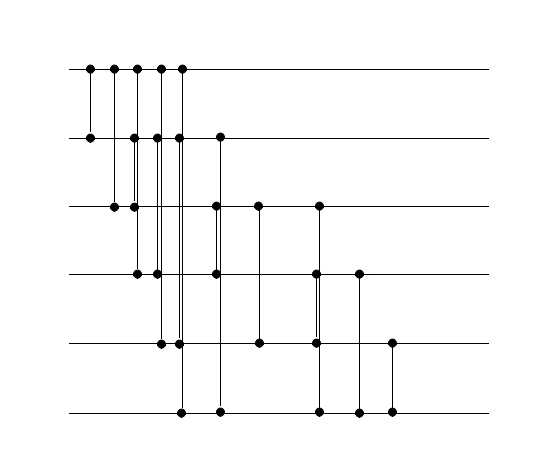
Сортировка выбором

Теорема:

В результирующей сети будет [math]\dfrac{n(n - 1)}{2}[/math] компараторов.

Доказательство:

[math]\triangleright[/math]

Воспользуемся принципом математической индукции. Базой индукции будет [math] n = 2 [/math] Шаг индукции: Рассмотрим метод построения сетей для сортировок выбором. Пусть [math] S(n) [/math] - количество компараторов в сети сортировки с [math] n [/math] входами, тогда для получения [math](n + 1)[/math]-й сети сортировки надо к предыдущей добавить компараторы: [math][n + 1; 1], [n; 1]\dots[3; 1], [2; 1] [/math]. Подсчитаем общее количество компараторов: [math]S(n + 1) = \dfrac{n(n - 1)}{2} + n = \dfrac{n(n + 1)}{2} [/math], заметим, что данное количество компараторов удовлетворяет нашему шагу индукции.

[math]\triangleleft[/math]

См.также

• Сортировочные сети с особыми свойствами

Источники информации

• Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0
• Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4.
• Википедия - Сети сортировки