Сортирующие сети для квадратичных сортировок — различия между версиями
Timur (обсуждение | вклад) |
Timur (обсуждение | вклад) |
||
| Строка 33: | Строка 33: | ||
Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки. | Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки. | ||
| − | При переходе от <tex>n</tex> | + | При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> дополнительных компараторов. В полученной "треугольной" сети можно заметить, что <tex>n - 1</tex> компаратор входят в уже существующие слои, но тогда один компаратор из предыдущей сортирующий сети и один из добавленных не вносят вклад в количество слоев. Тогда можно получить рекуррентное соотношение: <tex> S(n + 1) = S(n) + 2 </tex>. |
Данное рекуррентное соотношение имеет решение <tex> S(n) = 2n - 3 </tex>. Что и требовалось доказать. | Данное рекуррентное соотношение имеет решение <tex> S(n) = 2n - 3 </tex>. Что и требовалось доказать. | ||
| Строка 59: | Строка 59: | ||
Пусть <tex> S(n) </tex> - количество слоев в сети сортировки с <tex> n </tex> входами. | Пусть <tex> S(n) </tex> - количество слоев в сети сортировки с <tex> n </tex> входами. | ||
| − | При переходе от <tex>n</tex> | + | При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> компаратор. Заметим, что с <tex> n - 2 </tex> компараторами можно сделать слои, используя слои из предыдущей сортирующей сети. Это возможно сделать, т.к. <tex> n - 2 </tex> слоя из предыдущей сети вкладываются внутрь <tex> n - 2 </tex> новых компараторов, так, что они образуют новый слой. Тогда остается два компаратора, которые сами являются слоями. Тем самым получили рекуррентное соотношение: |
<tex> S(n + 1) = S(n) + 2 </tex> с начальными данными (<tex>S(2) = 1</tex>). Решением данного рекуррентного соотношения является <tex> S(n) = 2n - 3 </tex>. Что и требовалось доказать | <tex> S(n + 1) = S(n) + 2 </tex> с начальными данными (<tex>S(2) = 1</tex>). Решением данного рекуррентного соотношения является <tex> S(n) = 2n - 3 </tex>. Что и требовалось доказать | ||
Версия 19:35, 20 мая 2015
Рассмотрим модели сортирующих сетей для квадратичных сортировок.
Содержание
[убрать]Сортирующие сети с последовательной сортировкой
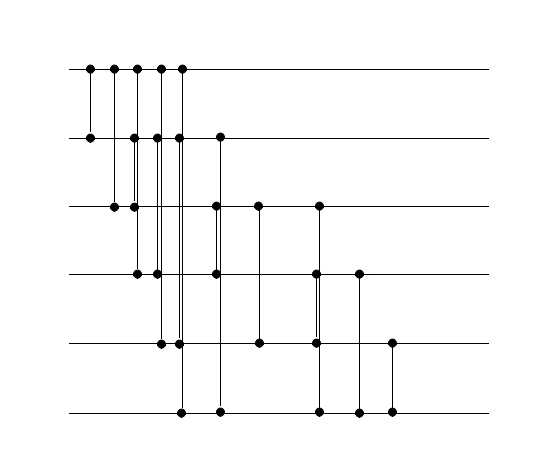
На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок.
| Сортировка пузырьком | Сортировка вставками | Сортировка выбором |
 |
 |
|
Сортирующие сети с параллельной сортировкой
На один слой будем устанавливать несколько компараторов.
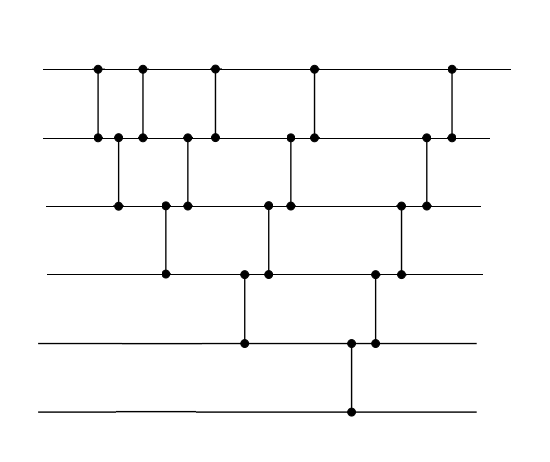
Сортировка пузырьком и вставками
Заметим, если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Этот факт легко заметить, сдвинув компараторы вправо и влево соответственно и разрешив выполнять одновременные вычисления.
| Теорема: |
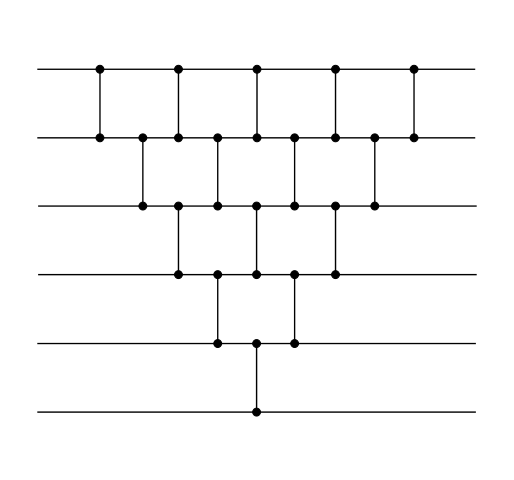
В результирующей сети будет слоев, где - количество входов. |
| Доказательство: |
|
Докажем данное утверждение по принципу математической индукции. База индукции: При . В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. Шаг индукции: Пусть — количество слоев в сети сортировки. При переходе от сортирующей сети с входами к сети с входами, добавляем дополнительных компараторов. В полученной "треугольной" сети можно заметить, что компаратор входят в уже существующие слои, но тогда один компаратор из предыдущей сортирующий сети и один из добавленных не вносят вклад в количество слоев. Тогда можно получить рекуррентное соотношение: . Данное рекуррентное соотношение имеет решение . Что и требовалось доказать. |
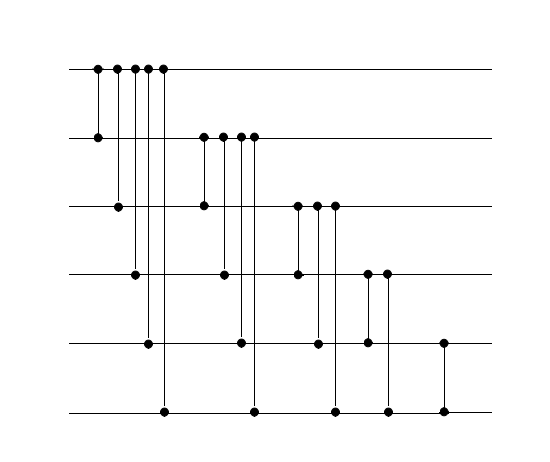
Сортирующая сеть для :
Сортировка выбором
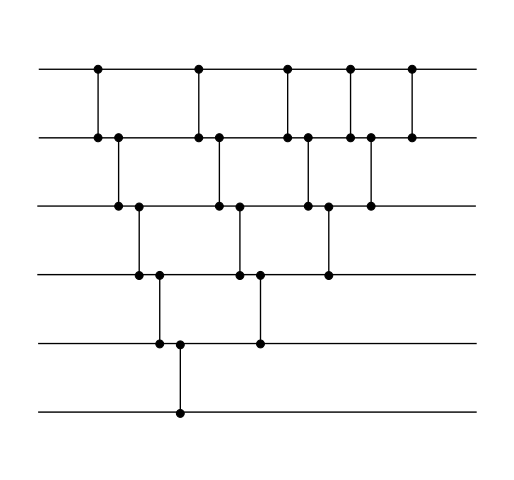
Будем объединять в слой
| Теорема: |
В результирующей сети будет слой, где — количество входов. |
| Доказательство: |
|
Воспользуемся принципом математической индукции. База индукции: . В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. Шаг индукции: Пусть - количество слоев в сети сортировки с входами. При переходе от сортирующей сети с входами к сети с входами, добавляем компаратор. Заметим, что с компараторами можно сделать слои, используя слои из предыдущей сортирующей сети. Это возможно сделать, т.к. слоя из предыдущей сети вкладываются внутрь новых компараторов, так, что они образуют новый слой. Тогда остается два компаратора, которые сами являются слоями. Тем самым получили рекуррентное соотношение: с начальными данными (). Решением данного рекуррентного соотношения является . Что и требовалось доказать |
См.также
Источники информации
- Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0
- Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4.
- Википедия - Сети сортировки