Сортирующие сети для квадратичных сортировок — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
Строка 32: Строка 32:
 
Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки.
 
Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки.
  
−
При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> дополнительных компараторов (<tex>[1:2],[2:3]\dots[n:n + 1]</tex> или <tex>[n + 1:n],[n:n + 1]\dots[1:2]</tex>, т.к. возможны две стратегии добавления). В полученной "треугольной" сети можно заметить, что <tex>n - 1</tex> компаратор входят в уже существующие слои (<tex>[2:3],[3:4]\dots[n:n + 1] </tex> или <tex>[n:n + 1],[n - 1:n - 2]\dots[2:3]</tex>).т.е. на каждом четном слое самым верхним компаратором будет <tex> [2:3] </tex>, а на нечетном <tex>[1:2]</tex>, но тогда один компаратор из предыдущей сортирующий сети и один из добавленных не вносят вклад в количество слоев. Тогда видно, что количество слоев увеличилось на <tex> 2 = S(n + 1) - S(n) </tex>, т.е. наш переход выполняется и формула верна. Что и требовалось доказать.
+
При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> дополнительных компараторов (<tex>[1:2],[2:3]\dots[n:n + 1]</tex> или <tex>[n + 1:n],[n:n + 1]\dots[1:2]</tex>, т.к. возможны две стратегии добавления). В полученной "треугольной" сети можно заметить, что <tex>n - 1</tex> компаратор входят в уже существующие слои (<tex>[2:3],[3:4]\dots[n:n + 1] </tex> или <tex>[n:n + 1],[n - 1:n - 2]\dots[2:3]</tex>) т.е. можно объединить компараторы в слои так, что в каждом четном слое самым верхним компаратором будет <tex> [2:3] </tex>, а на нечетном <tex>[1:2]</tex>,т.к. количество этих компараторов <tex> n - 1</tex> и <tex> n - 2 </tex> , но тогда один компаратор из предыдущей сортирующий сети и один из добавленных не вносят вклад в количество слоев. Тогда видно, что количество слоев увеличилось на <tex> 2 = S(n + 1) - S(n) </tex>, т.е. переход выполняется и формула верна. Что и требовалось доказать.
  
 
}}
 
}}

Версия 19:04, 24 мая 2015

Рассмотрим модели сортирующих сетей для квадратичных сортировок.

Сортирующие сети с последовательной сортировкой

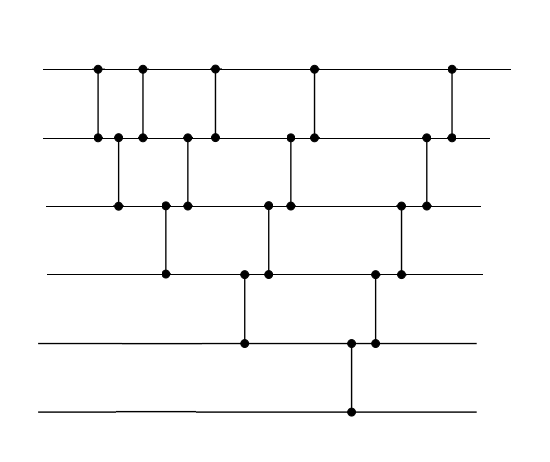
На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок.

Сортировка пузырьком Сортировка вставками Сортировка выбором
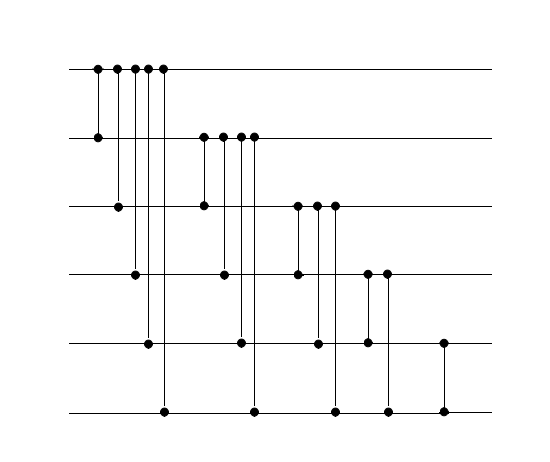
Bubblesort.png Insertsort.png Choosesort.png

Сортирующие сети с параллельной сортировкой

На один слой устанавливается несколько компараторов.

Сортировка пузырьком и вставками

Заметим, что если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Это видно из симметрии расположения компараторов на картинках выше.

Утверждение:
В результирующей сети будет [math](2n - 3)[/math] слоев, где [math]n[/math] — количество входов.
[math]\triangleright[/math]

Докажем данное утверждение по принципу математической индукции.

База индукции:

При [math] n = 2 [/math]. В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется.

Шаг индукции:

Пусть [math] S(n) = 2n - 3 [/math] — количество слоев в сети сортировки.

При переходе от сортирующей сети с [math]n[/math] входами к сети с [math]n + 1[/math] входами, добавляем [math] n [/math] дополнительных компараторов ([math][1:2],[2:3]\dots[n:n + 1][/math] или [math][n + 1:n],[n:n + 1]\dots[1:2][/math], т.к. возможны две стратегии добавления). В полученной "треугольной" сети можно заметить, что [math]n - 1[/math] компаратор входят в уже существующие слои ([math][2:3],[3:4]\dots[n:n + 1] [/math] или [math][n:n + 1],[n - 1:n - 2]\dots[2:3][/math]) т.е. можно объединить компараторы в слои так, что в каждом четном слое самым верхним компаратором будет [math] [2:3] [/math], а на нечетном [math][1:2][/math],т.к. количество этих компараторов [math] n - 1[/math] и [math] n - 2 [/math] , но тогда один компаратор из предыдущей сортирующий сети и один из добавленных не вносят вклад в количество слоев. Тогда видно, что количество слоев увеличилось на [math] 2 = S(n + 1) - S(n) [/math], т.е. переход выполняется и формула верна. Что и требовалось доказать.
[math]\triangleleft[/math]

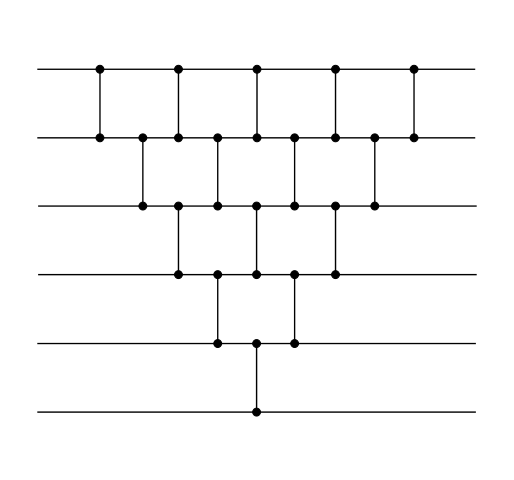
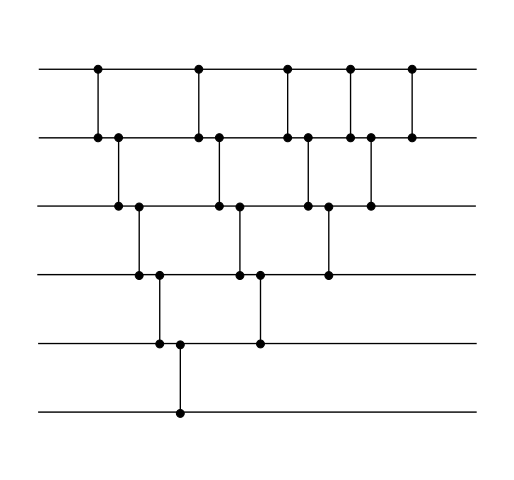
Сортирующая сеть для [math] n = 6 [/math]:

Parralelsort.png

Сортировка выбором

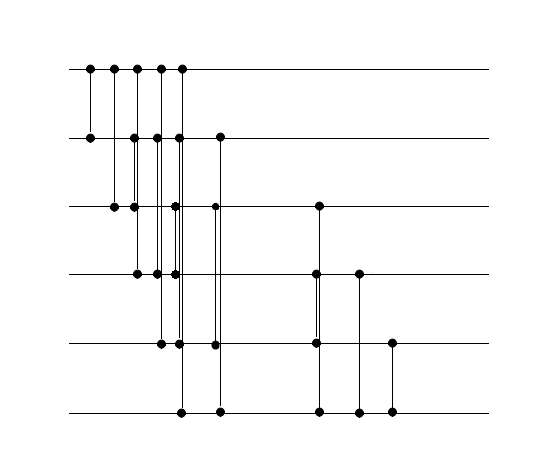
Сеть для сортировки выбором выглядит иначе. При переходе к сети с [math] n + 1 [/math] входами, добавляется [math] n [/math] компараторов: [math] [0:1],[0:2]\dots[0:n] [/math].

Choosesortparralel2.png

Утверждение:
В результирующей сети будет [math]2n - 3[/math] слоев, где [math] n [/math] — количество входов.
[math]\triangleright[/math]

Определим операцию вложения компаратора [math] [i:j] [/math] в компаратор [math] [t:s] [/math] : разместим компаратор [math] [i:j] [/math] и [math] [t:s] [/math] на одном слое, так, что [math] t \lt i \lt j \lt s [/math].

Теперь воспользуемся принципом математической индукции.

База индукции:

[math] n = 2 [/math]. В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется.

Шаг индукции:

Пусть [math] S(n) [/math] — количество слоев в сети сортировки с [math] n [/math] входами.

При переходе от сортирующей сети с [math]n[/math] входами к сети с [math]n + 1[/math] входами, добавляем [math] n [/math] компараторов [math]\left( [0:1] \dots [0:n]\right) [/math]. Заметим, что в [math] n - 2 [/math] добавленных компаратора можно вложить [math] n - 2 [/math] компараторов из предыдущей сети, так, вкладывая один компаратор в другой, образуется новый слой, т.е. количество слоев не изменяется. Тогда останется два компаратора: [math][0:1], [0:2] [/math] в которые ничего нельзя вложить, т.е. количество слоев изменяется на [math] 2 = S(n + 1) - S(n) [/math].

Тогда наш переход выполняется и формула верна. Что и требовалось доказать.
[math]\triangleleft[/math]

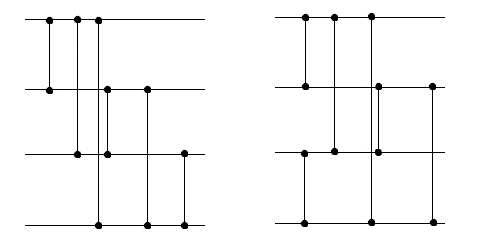
Пример правильной и ошибочной сети для [math] n = 4 [/math]. Если перенести свободные компараторы и слить их в один слой, то можно уменьшить количество слоев, но при этом сеть перестает быть сортирующей (при [math] n = 4 [/math] ошибка будет возникать на последовательности [math] [0,1,0,0] [/math]).

MyRis.jpg

См.также

Источники информации

  • Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0
  • Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4.
  • Википедия — Сети сортировки
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Сортирующие_сети_для_квадратичных_сортировок&oldid=46851»