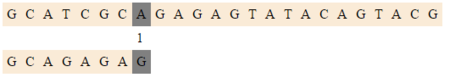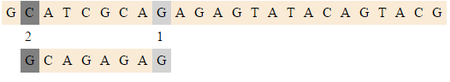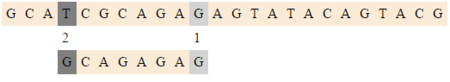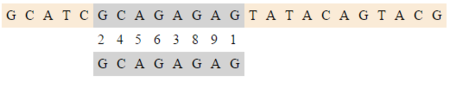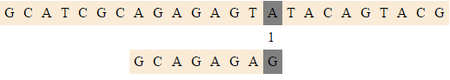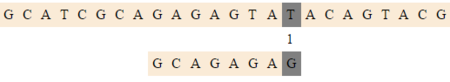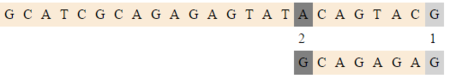Алгоритм Райта — различия между версиями
(→Асимптотика) |
Zernov (обсуждение | вклад) (→Пример) |
||
| Строка 80: | Строка 80: | ||
==Пример== | ==Пример== | ||
| + | Пусть нам дана строка <tex>y = GCATCGCAGAGAGTATACAGTACG</tex> и образец <tex>x=GCAGAGAG</tex> | ||
| + | |||
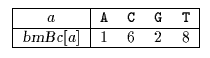
| + | [[Файл:RaitaPre.png|thumb|center|Массив <tex>bmBc</tex> после фазы препроцессинга]] | ||
| + | |||
| + | |||
| + | [[Файл:Raita1.png|thumb|450px|center|Сдвигаемся на <tex>1 (bmBc[A])</tex> после сравнения]] | ||
| + | |||
| + | [[Файл:Raita2.png|thumb|450px|center|Сдвигаемся на <tex>2 (bmBc[G])</tex> после второго сравнения]] | ||
| + | |||
| + | [[Файл:Raita3.png|thumb|450px|center|Сдвигаемся на <tex>2 (bmBc[G])</tex>]] | ||
| + | |||
| + | [[Файл:Raita4.png|thumb|450px|center|Сдвигаемся на <tex>2 (bmBc[G])</tex> после всех сравнений]] | ||
| + | |||
| + | [[Файл:Raita5.png|thumb|450px|center|Сдвигаемся на <tex>1 (bmBc[A])</tex>]] | ||
| + | |||
| + | [[Файл:Raita6.png|thumb|450px|center|Сдвигаемся на <tex>8 (bmBc[T])</tex>]] | ||
| + | |||
| + | [[Файл:Raita7.png|thumb|450px|center|Сдвигаемся на <tex>2 (bmBc[G])</tex>]] | ||
| + | |||
| + | В итоге, чтобы найти одно вхождение образца длиной <tex>m = 8</tex> в образце длиной <tex>n = 24</tex> нам понадобилось <tex>18</tex> сравнений символов | ||
==Источники информации== | ==Источники информации== | ||
Версия 18:37, 21 марта 2016
Алгоритм Райта — алгоритм поиска подстроки в строке, который опубликовал Тим Райта в 1991 году, являющийся модификацией алгоритма Бойера-Мура и улучшающий его асимптотику
Описание алгоритма
Алгоритм Райта ищет образец в заданном тексте сравнивания их символы. Сравнение происходит в следующем порядке (окном текста будем называть последовательность символов , где — длина образца ):
- Последний символ образца сравнивается с самым правым символом окна.
- Если они совпадают, то первый символ сравнивается с самым левым символом окна.
- Если они опять совпали, то сравниваются символы, находящиеся по середине образца и окна.
Если все шаги прошли успешно, то начинаем сравнивать образец и текст посимвольно в обычном порядке, начиная с второго с конца символа. В противном случае, выполняем функцию сдвига плохого символа, которая обрабона в стадии препроцессинга. Эта функция аналогична той, которая была использована в фазе препроцессинга алгоритма Бойера-Мура.
Псевдокод
void RAITA(char[] x, int m, char[] y, int n) {
int[] bmBc
char c, firstCh, middleCh, lastCh;
if (m == 0)
return
else if (m == 1) {
//Проверка на случай поиска вхождения одного символа
int match = 0
while (match < n) {
match = findFirst(y, match, n - 1, x[0])
if (match != -1) {
print(match)
}
else
print("No matches")
return
}
}
int findFirst(char[] y, int fromIndex, int toIndex, char symbol){
for (i = fromIndex .. toIndex){
if (y[i] == symbol){
return i
}
}
return -1
}
boolean restEquals(char[] y, int fromIndex, char[] x, int toIndex){
for (i = fromIndex .. toIndex){
if (y[i] != x[i - fromIndex + 1]){
return false
}
}
return true
}
//Стадия препроцессинга
int[] preBmBc(char[] x, int m) {
int[] result = int[m]
for (i = 0 .. m - 1){
result[i] = m;
}
for (i = 0 .. m - 2){
result[x[i]] = m - i - 1;
}
return result
}
bmBc = preBmBc (x, m)
firstCh = x[0];
middleCh = x[m/2];
lastCh = x[m - 1];
//Поиск
int j = 0
while (j <= n - m) {
c = y[j + m - 1]
if (lastCh == c && middleCh == y[j + m / 2] && firstCh == y[j] &&
restEquals(y, j + 1, x, j + m - 2)){
print(j)
return
}
j += bmBc[c];
}
print("No matches")
}
Асимптотика
- Фаза препроцессинга требует времени и памяти
- В худшем случае поиск требует сравнений.
Пример
Пусть нам дана строка и образец
В итоге, чтобы найти одно вхождение образца длиной в образце длиной нам понадобилось сравнений символов
Источники информации
- RAITA T., 1992, Tuning the Boyer-Moore-Horspool string searching algorithm, Software - Practice & Experience, 22(10):879-884.
- Raita algorithm
- Raita algorithm на англ вики