Теорема о нижней оценке для сортировки сравнениями

Сортировка сравнениями (англ. Comparison sort) — алгоритм сортировки, который совершает операции сравнения элементов, но никак не использует их внутреннюю структуру.

Теорема (о нижней оценке для сортировки сравнениями):

В худшем случае любой алгоритм сортировки сравнениями выполняет [math]\Omega(n \log n)[/math] сравнений, где [math]n[/math] — число сортируемых элементов.

Доказательство:

[math]\triangleright[/math]

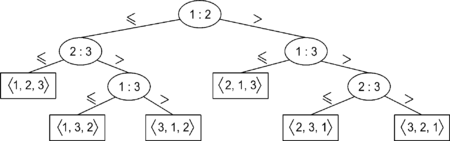
Пример дерева для алгоритма сортировки трех элементов. Внутренний узел, помеченный как [math] i:j [/math], указывает сравнение между [math] a_{i} [/math] и [math] a_{j} [/math]. Лист, помеченный перестановкой [math] \left \langle \pi(1), \pi(2), \ldots , \pi(n) \right \rangle [/math], указывает упорядочение [math] a_{\pi(1)} \leqslant a_{\pi(2)} \leqslant \ldots \leqslant a_{\pi(n)} [/math]. Любому алгоритму сортировки сравнениями можно сопоставить дерево. В нем узлам соответствуют операции сравнения элементов, ребрам — переходы между состояниями алгоритма, а листьям — конечные перестановки элементов (соответствующие завершению алгоритма сортировки). Необходимо доказать, что высота такого дерева для любого алгоритма сортировки сравнениями не меньше чем [math]\Omega(n \log n)[/math], где [math]n[/math] — количество элементов. Ограничимся рассмотрением сортировки перестановок [math]n[/math] элементов. При сравнении некоторых двух из них, существует два возможных исхода ([math]a_i \lt a_j[/math] и [math]a_i \gt a_j[/math]), значит, каждый узел дерева имеет не более двух сыновей. Всего существует [math]n![/math] различных перестановок [math]n[/math] элементов, значит, число листьев нашего дерева не менее [math]n![/math] (в противном случае некоторые перестановки были бы не достижимы из корня, а, значит, алгоритм не правильно работал бы на некоторых исходных данных). Докажем, что двоичное дерево с не менее чем [math]n![/math] листьями имеет глубину [math]\Omega(n \log n)[/math]. Легко показать, что двоичное дерево высоты [math]h[/math] имеет не более чем [math]2^h[/math] листьев. Значит, имеем неравенство [math]n! \leqslant l \leqslant 2^h[/math], где [math]l[/math] — количество листьев. Прологарифмировав его, получим: [math] h \geqslant \log_2 n! = \log_2 1 + \log_2 2 + \ldots + \log_2 n \gt [/math] [math] \dfrac{n}{2} \log_2 (\dfrac{n}{2}) = \dfrac{n}{2}(\log_2 n - 1) = \Omega (n \log n)[/math] Итак, для любого алгоритма сортировки сравнениями, существует такая перестановка, на которой он выполнит [math]\Omega(n \log n)[/math] сравнений, ч. т. д.

[math]\triangleleft[/math]

Следствия

Утверждение:

Пирамидальная сортировка и сортировка слиянием являются асимптотически оптимальными сортировками сравнением.

[math]\triangleright[/math]

Верхние границы [math] O(n \log n) [/math] времени работы пирамидальной сортировки и сортировки слиянием совпадают с нижней границей [math]\Omega(n \log n)[/math] для наихудшего случая из теоремы о нижней границе для сортировки сравнениями.

[math]\triangleleft[/math]

Утверждение:

Не существует структуры данных, которая одновременно поддерживает добавление элементов и извлечение минимума за амортизированное время [math] O(1) [/math].

[math]\triangleright[/math]

Пусть имеется структура данных, которая поддерживает добавление элемента за время [math] O(1) [/math]. При этом значение минимального элемента может измениться, что потребует сортировки элементов для его извлечения. Согласно теореме минимальное время для этого составляет [math] \Omega (n \log n) [/math]. Обратно, если имеется структура данных, которая поддерживает извлечение минимального элемента за время [math] O(1) [/math], требуется по крайней мере [math] O(\log n) [/math] времени для каждой операции добавления элемента с целью поддержания элементов структуры в отсортированном виде.

[math]\triangleleft[/math]

Источники информации

• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с
• Андрей Калинин Сортировка за линейное время
• Конспект по курсу "Алгоритмы и алгоритмические языки" (доказательство теоремы через формулу Стирлинга).
• Лекториум "Алгоритмы сортировки"