Лемма Огдена — различия между версиями
Vsklamm (обсуждение | вклад) (→Источники информации) |
|||
| (не показана 31 промежуточная версия 12 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Для бесконечного языка применение приведённых в предыдущем разделе приёмов приведёт к началу построения в общем случае бесконечного числа правил грамматики. Требуется более мощный аппарат, которым служит доказываемая ниже лемма Огдена. | ||
| + | |||
| + | == Лемма == | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Для каждой [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно- | + | Для каждой [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно-свободной грамматики]] <tex>\Gamma =\langle \Sigma, N, S \in N, P \subset N\times (\Sigma\cup N)^{*}\rangle</tex> существует такое <tex>n</tex>, что для любого слова <tex>\omega \in L(\Gamma)</tex> длины не менее <tex>n</tex> и для любых выделенных в <tex>\omega</tex> не менее <tex>n</tex> позиций, <tex>\omega</tex> может быть представлено в виде <tex>\omega=uvxyz</tex>, причем: |
| − | # <tex>x</tex> содержит выделенную позицию | + | # <tex>x</tex> содержит выделенную позицию; |
# либо <tex>u</tex> и <tex>v</tex>, либо <tex>y</tex> и <tex>z</tex> обе содержат выделенные позиции; | # либо <tex>u</tex> и <tex>v</tex>, либо <tex>y</tex> и <tex>z</tex> обе содержат выделенные позиции; | ||
# <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций; | # <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций; | ||
| − | # существует <tex>A \in | + | # существует <tex>A \in N</tex>, такой что <tex>S \Rightarrow^{+} uAz \Rightarrow^{+} uvAyz \Rightarrow^{+} uvxyz</tex>. (т.е. <tex>\forall k \geqslant 0~uv^{k}xy^{k}z\in L</tex>) |
|proof= | |proof= | ||
| − | Введем следующие обозначения: <tex>m = |N|</tex> и <tex>l</tex> — длина самой длинной правой части правила из <tex>P</tex>. Тогда в качестве <tex>n</tex> возьмем <tex>l^{2m + 3}</tex>. Рассмотрим дерево разбора <tex>T</tex> для произвольного слова <tex>\omega \in L(\Gamma)</tex>, у которого <tex>|\omega| \ | + | Введем следующие обозначения: <tex>m = |N|</tex> и <tex>l</tex> — длина самой длинной правой части правила из <tex>P</tex>. Тогда в качестве <tex>n</tex> возьмем <tex>l^{2m + 3}</tex>. Рассмотрим дерево разбора <tex>T</tex> для произвольного слова <tex>\omega \in L(\Gamma)</tex>, у которого <tex>|\omega| \geqslant n</tex>. В силу выбора <tex>n</tex> в <tex>T</tex> будет по крайне мере один путь от корня до листа длины не менее <tex>2m + 3</tex>. Произвольным образом выделим в <tex>\omega</tex> не менее <tex>n</tex> позиций. Соответствующие этим позициям листья дерева <tex>T</tex> будем называть выделенными. |
| + | |||
| + | Пусть <tex>v_1</tex> — корень <tex>T</tex>, а <tex>v_{i + 1}</tex> — сын <tex>v_i</tex>, который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то <tex>v_{i + 1}</tex> самый правый из них). Рассмотрим <tex>v_1, v_2, \ldots, v_p</tex> {{---}} путь от корня до листа. | ||
| + | |||
| + | Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Докажем по индукции, что если среди <tex>v_1, v_2, \ldots, v_i</tex> вершин есть <tex>k</tex> ветвящихся, то <tex>v_{i + 1}</tex> имеет хотя бы <tex>l^{2m + 3 - k}</tex> выделенных потомков. <br>База индукции: <tex>i = 0</tex>. Тогда <tex>k = 0</tex> и <tex>v_1</tex> имеет по крайне мере <tex>n</tex> выделенных потомков, поскольку является корнем. <br>Индукционный переход. Если <tex>v_i</tex> не является ветвящейся вершиной, то <tex>v_{i + 1}</tex> имеет такое же число ветвящихся потомков, как и <tex>v_i</tex>. Если <tex>v_i</tex> — ветвящаяся вершина, то <tex>v_{i + 1}</tex> имеет не более чем в <tex>l</tex> раз меньшее число выделенных потомков. | ||
| + | |||
| + | Поскольку <tex>v_1</tex> имеет хотя бы <tex>n = l^{2m + 3}</tex> выделенных потомков, то <tex>v_1, v_2, \ldots, v_p</tex> содержит по крайне мере <tex>2m + 3</tex> ветвящиеся вершин. Заметим, что <tex>v_p</tex> {{---}} лист, поэтому <tex>p > 2m + 3</tex>. | ||
| + | |||
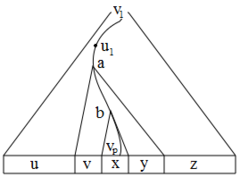
| + | [[Файл:derivation_tree_T.png|240px|thumb|left|Дерево вывода <tex>T</tex>]]Будем называть <tex>v_i</tex> левой ветвящейся вершиной, если ее сын, не принадлежащий пути <tex>v_1, v_2, \ldots, v_p</tex>, имеет выделенного потомка, лежащего слева от <tex>v_p</tex>. В противном случае назовем <tex>v_i</tex> правой ветвящейся вершиной. Рассмотрим последние <tex>2m + 3</tex> вершины, принадлежащие пути <tex>v_1, v_2, \ldots, v_p</tex>. Предположим, что хотя бы <tex>m + 2</tex> вершины {{---}} левые ветвящиеся (случай, когда хотя бы <tex>m + 2</tex> вершины {{---}} правые ветвящиеся, разбирается аналогично). Пусть <tex>u_1, u_2, \ldots, u_{m + 2}</tex> {{---}} последние <tex>m + 2</tex> левые ветвящиеся вершины. Поскольку <tex>m = |N|</tex>, то среди них можно найти как минимум две вершины, соответствующие одному нетерминалу. Обозначим эти вершины <tex>a</tex> и <tex>b</tex>, причем <tex>b</tex> {{---}} потомок <tex>a</tex>. Тогда на рисунке показано, как представить <tex>\omega</tex> в требуемом виде. | ||
| + | |||
| + | |||
| + | Условие <tex>(1)</tex> выполнено, поскольку <tex>x</tex> содержит выделенную вершину, а именно <tex>v_p</tex>. Очевидно, что условие <tex>(4)</tex> выполнено в силу предложенного разбиения <tex>\omega</tex>. Кроме того, <tex>u</tex> содержит выделенную вершину, а именно потомка некоторого сына вершины <tex>u_1</tex>. Аналогично, выделенный потомок некоторого сына вершины <tex>a</tex> содержится в <tex>v</tex>. Таким образом, условие <tex>(2)</tex> выполнено. Поскольку между <tex>v_p</tex> и <tex>a</tex> не более <tex>2m + 3</tex> вершин, вершина <tex>a</tex> имеет не более <tex>n</tex> выделенных потомков, поэтому условие <tex>(3)</tex> выполнено. | ||
| + | }} | ||
| + | |||
| + | == Примеры не КС-языка, для которого выполняется лемма == | ||
| + | Следует обратить особое внимание на то, что лемма содержит лишь необходимые условия принадлежности КС языку. | ||
| + | ===Пример <tex> 1 </tex>=== | ||
| + | {{Утверждение | ||
| + | |statement=Можно построить такой язык, для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным. | ||
| + | |proof= | ||
| + | При анализе этого языка следует использовать алгебраические свойства множества. Выберем <tex>P</tex> {{---}} подмножество <tex>N</tex> и | ||
| + | |||
| + | <tex>A_{p} = \{ (ab)^n \mid P \in N \} </tex> | ||
| + | |||
| + | <tex>B_{p} = A_{p} \cup X^* \{aa, bb\}X^*</tex> | ||
| + | |||
| + | Языки над <tex>X=\{a, b\}</tex>. | ||
| + | |||
| + | Очевидно, что <tex>B_{p}</tex> {{---}} КС, если <tex>A_{p}</tex> контекстно-свободен. <tex>B_{p}</tex> является рекурсивно-перечислимым, если и <tex>A_{p}</tex> им является. | ||
| + | |||
| + | Для <tex>B_{p}</tex> будет выполняться лемма Огдена при <tex>n = 4</tex>. Выбрав <tex>A_{p}</tex> таким образом, чтобы он был рекурсивно-перечислимым, мы создадим язык для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным. (Такие языки существуют)<ref>A.V. Aho & J.D. Ullman, The Theory of Parsing, Translation and Compilimg, Vol. I, 1972</ref> | ||
| + | }} | ||
| − | + | === Пример <tex> 2 </tex> === | |
| + | {{Утверждение | ||
| + | |statement=Язык <tex>L = {a^mb^nc^l}</tex>, где <tex> m, n, l </tex> {{---}} попарно различны, не является КС-языком. | ||
| + | |proof= | ||
| − | + | Предположим, что данный язык контекстно-свободный. Возьмем цепочку <tex>\omega = a^kb^{k+(k-1)!} c^{k+k!}</tex>, где <tex>k</tex> {{---}} константа из леммы Огдена, выделив в ней все вхождения символа <tex>a</tex>. Тогда при представлении цепочки <tex>\omega</tex> в виде <tex>uvxyz</tex> цепочка <tex>x</tex> (по условию (1) леммы) обязательно «зацепит» хотя бы один | |
| + | символ <tex>a</tex>. Cледовательно, цепочка <tex>v</tex> состоит только из символов <tex>a</tex> (как и цепочка <tex>u</tex>). А именно, | ||
| + | <tex>v = \alpha^p</tex>, <tex>1 \leqslant p \leqslant k+1</tex>. | ||
| − | + | Тогда, если цепочка <tex>x</tex> содержит и другие символы, кроме <tex>a</tex>, цепочка <tex>y</tex> может входить либо в «зону» символов <tex>b</tex> (целиком), либо в «зону» символов <tex>c</tex> (целиком), так как расположение накачиваемых цепочек на стыках зон, очевидно, невозможно. В первом случае «кратность» <tex>\alpha</tex> накачки цепочки <tex>v</tex>, которая уравняет числа символов <tex>a</tex> и <tex>c</tex>, определяется из соотношения: | |
| + | <tex>k + \alpha \cdot p = k + k!</tex>, то есть <tex>\alpha = \dfrac{k!}{p} </tex> | ||
| − | + | Во втором случае <tex>\dfrac {k-1!}{p}</tex> - кратная накачка цепочки <tex>v</tex> уравняет числа вхождений символов <tex>a</tex> и <tex>b</tex>. | |
| + | Не исключено, наконец, что обе накачиваемые цепочки расположены в «зоне» символов <tex>a</tex>. Но тогда одним из указанных выше способов накачки можно уравнять числа либо символов <tex>a</tex> и <tex>b</tex>, либо <tex>a</tex> и <tex>c</tex>. | ||
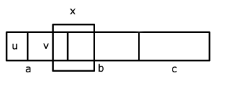
| + | [[Файл:Ogden1.png|left|Рис. Цепочки контекстно-свободного языка]] | ||
| − | + | Заметим, что возможность выделения символов существенно упрощает анализ данного языка, так как позволяет считать, что цепочка <tex>v</tex> может расположиться единственным способом. Иначе, т.е. при использовании леммы о разрастании для кс-языков, решение задачи было бы, по меньшей мере, сильно затруднено. | |
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | *[[Лемма_о_разрастании_для_КС-грамматик|Лемма о разрастании для КС-грамматик]] | ||
| + | |||
| + | ==Примечания== | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | == Источники информации == | ||
| + | |||
| + | * [http://ru.wikipedia.org/wiki/Лемма_Огдена Wikipedia {{---}} Лемма Огдена] | ||
| + | * ''Hopcroft, Motwani and Ullman'' {{---}} Automata Theory, Languages, and Computation {{---}} Addison-Wesley, 1979. ISBN 81-7808-347-7. | ||
| + | * ''Ogden, W.'' (1968). A helpful result for proving inherent ambiguity. Mathematical Systems Theory. 2 (3): 191–194. | ||
| + | * [http://archive.numdam.org/ARCHIVE/ITA/ITA_1978__12_3/ITA_1978__12_3_201_0/ITA_1978__12_3_201_0.pdf On languages satisfying Ogden's lemma] | ||
| + | * [http://ccf.ee.ntu.edu.tw/~yen/courses/toc14/chapter-2a.pdf Ogden's lemma] | ||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Контекстно-свободные грамматики]] | ||
| + | [[Категория: Опровержение контекстно-свободности языка]] | ||
Версия 16:17, 2 апреля 2018
Для бесконечного языка применение приведённых в предыдущем разделе приёмов приведёт к началу построения в общем случае бесконечного числа правил грамматики. Требуется более мощный аппарат, которым служит доказываемая ниже лемма Огдена.
Содержание
Лемма
| Лемма: |
Для каждой контекстно-свободной грамматики существует такое , что для любого слова длины не менее и для любых выделенных в не менее позиций, может быть представлено в виде , причем:
|
| Доказательство: |
|
Введем следующие обозначения: и — длина самой длинной правой части правила из . Тогда в качестве возьмем . Рассмотрим дерево разбора для произвольного слова , у которого . В силу выбора в будет по крайне мере один путь от корня до листа длины не менее . Произвольным образом выделим в не менее позиций. Соответствующие этим позициям листья дерева будем называть выделенными. Пусть — корень , а — сын , который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то самый правый из них). Рассмотрим — путь от корня до листа. Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Докажем по индукции, что если среди вершин есть ветвящихся, то имеет хотя бы выделенных потомков. Поскольку имеет хотя бы выделенных потомков, то содержит по крайне мере ветвящиеся вершин. Заметим, что — лист, поэтому . Будем называть левой ветвящейся вершиной, если ее сын, не принадлежащий пути , имеет выделенного потомка, лежащего слева от . В противном случае назовем правой ветвящейся вершиной. Рассмотрим последние вершины, принадлежащие пути . Предположим, что хотя бы вершины — левые ветвящиеся (случай, когда хотя бы вершины — правые ветвящиеся, разбирается аналогично). Пусть — последние левые ветвящиеся вершины. Поскольку , то среди них можно найти как минимум две вершины, соответствующие одному нетерминалу. Обозначим эти вершины и , причем — потомок . Тогда на рисунке показано, как представить в требуемом виде.
|
Примеры не КС-языка, для которого выполняется лемма
Следует обратить особое внимание на то, что лемма содержит лишь необходимые условия принадлежности КС языку.
Пример
| Утверждение: |
Можно построить такой язык, для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным. |
|
При анализе этого языка следует использовать алгебраические свойства множества. Выберем — подмножество и
Языки над . Очевидно, что — КС, если контекстно-свободен. является рекурсивно-перечислимым, если и им является. Для будет выполняться лемма Огдена при . Выбрав таким образом, чтобы он был рекурсивно-перечислимым, мы создадим язык для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным. (Такие языки существуют)[1] |
Пример
| Утверждение: |
Язык , где — попарно различны, не является КС-языком. |
|
Предположим, что данный язык контекстно-свободный. Возьмем цепочку , где — константа из леммы Огдена, выделив в ней все вхождения символа . Тогда при представлении цепочки в виде цепочка (по условию (1) леммы) обязательно «зацепит» хотя бы один символ . Cледовательно, цепочка состоит только из символов (как и цепочка ). А именно, , . Тогда, если цепочка содержит и другие символы, кроме , цепочка может входить либо в «зону» символов (целиком), либо в «зону» символов (целиком), так как расположение накачиваемых цепочек на стыках зон, очевидно, невозможно. В первом случае «кратность» накачки цепочки , которая уравняет числа символов и , определяется из соотношения: , то есть Во втором случае - кратная накачка цепочки уравняет числа вхождений символов и . Не исключено, наконец, что обе накачиваемые цепочки расположены в «зоне» символов . Но тогда одним из указанных выше способов накачки можно уравнять числа либо символов и , либо и . Заметим, что возможность выделения символов существенно упрощает анализ данного языка, так как позволяет считать, что цепочка может расположиться единственным способом. Иначе, т.е. при использовании леммы о разрастании для кс-языков, решение задачи было бы, по меньшей мере, сильно затруднено. |
См. также
Примечания
- ↑ A.V. Aho & J.D. Ullman, The Theory of Parsing, Translation and Compilimg, Vol. I, 1972
Источники информации
- Wikipedia — Лемма Огдена
- Hopcroft, Motwani and Ullman — Automata Theory, Languages, and Computation — Addison-Wesley, 1979. ISBN 81-7808-347-7.
- Ogden, W. (1968). A helpful result for proving inherent ambiguity. Mathematical Systems Theory. 2 (3): 191–194.
- On languages satisfying Ogden's lemma
- Ogden's lemma