Список с пропусками

Пример списка с пропусками

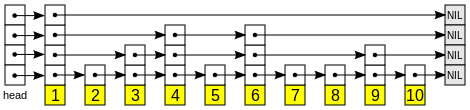
Список с пропусками (англ. skip list) — вероятностная структура данных, позволяющая в среднем за [math]O(\log(n))[/math] времени выполнять операции добавления, удаления и поиска элементов.

Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть [math]-[/math] на третьем и так далее, но при этом известно, что если элемент расположен на уровне [math]i[/math], то он также расположен на всех уровнях с номерами меньших [math]i[/math].

Построение

Односвязный отсортированный список

Получившийся список с пропусками

Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за [math]O(\log{n})[/math] времени выполнять операции добавления, удаления и поиска элементов.

На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне [math]-[/math] всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни.

Псевдокод

Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которое есть начало [math]\mathtt{head}[/math] и конец [math]\mathtt{tail}[/math]. Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне.

Элементы односвязного списка [math]-[/math] вершины [math]\mathtt{node}[/math], у которых есть [math]3[/math] поля:

• [math]\mathtt{next}[/math] [math]-[/math] ссылка на следующий элемент списка
• [math]\mathtt{key}[/math] [math]-[/math] ключ, который хранится в данной вершине
• [math]\mathtt{down}[/math] [math]-[/math] ссылка на соответственный элемент, лежащий уровнем ниже

Также известно, что [math]\mathtt{head{.}key} = -\infty \ [/math] и [math]\mathtt{tail{.}key} = \infty[/math].

Функция [math]\ \mathtt{build\_lvl} \ [/math] возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня.

   list build_lvl (list lvl)                   // Отсеивание нечётных элементов
       list next_lvl 
       node i = lvl.head                       // Перебор всех элементов lvl
       while (i != null) and (i != lvl.tail)
           next_lvl.push_back(node(i.key, i))  // Конструктор node(key, down) возвращает новую вершину с ключом key и ссылкой down на соответствующую вершину предыдущего уровеня
           i = i.next.next                     // Переход к следующему чётному элементу
       return next_lvl 

Функция [math]\ \mathtt{skip\_list} \ [/math] принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе.

   list skip_list (list l):
       list lvl = build_lvl(l)                // Построение первого уровня
       while lvl.size > 2                     // Добавление следующих уровней; последний содержит не более двух элементов
           lvl = build_lvl(lvl)                       
       return lvl                             // Возвращает ссылку на начало верхнего уровня

Операции над структурой

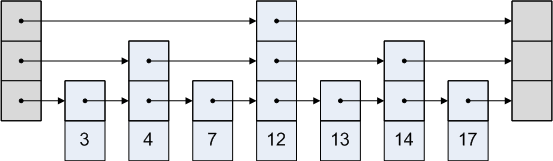
Поиск элемента

Пример поиска числа [math]8[/math]

Алгоритм поиска элементе в списке с пропусками состоит из следующих операций:

1. Начинаем поиск элемента в самом верхнем уровне
2. Переходим к следующему элементу списка, пока значение в следующей ячейке меньше
3. Переместиться на один уровень вниз и перейти к шагу [math]2[/math]. Если мы уже на первом уровне [math]-[/math] прекратить поиск и вернуть ссылку на текущую вершину

В конце алгоритма функция вернёт элемент, значение которого не меньше ключа [math]\mathtt{key}[/math] или ссылку на хвост списка на первом уровне.

Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет [math]\log{n}[/math] уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Уровней всего [math]\log{n}[/math], откуда вытекает оценка времени поиска элемента в [math]O(\log{n})[/math].

Псевдокод

Функция [math]\mathtt{find}[/math] возвращает ссылку на элемент, значение которого не меньше [math]\mathtt{key}[/math]. В случае, если все элементы в списке с пропусками меньше [math]\mathtt{key}[/math], то возвращается ссылка на конец списка с пропусками.

   T find (node res, K key)
       while res.key < key                                        // Пока значение вершины меньше ключа
           res = res.next()                                       // Перейдём к следующей вершине в текущем уровне
       if res.down = null                                         // Если мы находимся на первом уровне
           return res                                             // Мы нашли искомый элемент
       return find(res.down, key)                                 // Иначе спустимся на один уровень ниже

Для того, чтобы найти элемент с ключом [math]\mathtt{key}[/math] в списке с пропусками [math]\mathtt{list}[/math] необходимо запустить [math]\mathtt{find}[/math] следующим образом

   find(list.head(), key)

Вставка элемента

Для того, чтобы вставить элемент в список с пропусками, нужно запустить рекурсивную функцию, которая в каждом из уровней найдёт позицию, где должен был стоять элемент. Если это первый уровень, то просто вставляем элемент в список, а также бросаем монетку и возвращаем результат. Если же это не самый нижний уровень, то рекурсивно вызываем функцию, которая обрабатывает следующий уровень. Если в результате броска монетки на нижнем уровне выпал «Орёл», то вставляем элемент в список текущего уровня, а также снова кидаем монетку и возвращаем результат броска. Если же выпала «Решка», то просто возвращаем такой же результат. Нужно также обработать случай, когда на всех уровнях выпал «Орёл». В таком случае надо создать новый верхний уровень и вставить в него текущий элемент, а также присвоить списку с пропусками ссылку на начало самого верхнего списка.

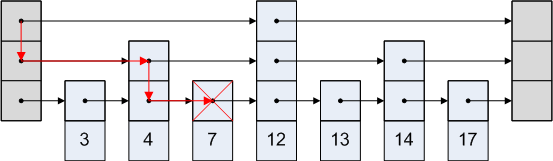
Удаление элемента

Для того, чтобы удалить элемент из списка с пропусками необходимо вызвать рекурсивную функцию, которая в каждом уровне, подобно поиску, найдёт позицию, где должен был стоять элемент. Во время рекурсии если это самый нижний уровень, то удаляем элемент из списка (не забывая при этом сохранить связность списка). Если это не это первый уровень, то рекурсивно вызовем функцию от уровня ниже, а также удалим элемент в текущем уровне. После удаления элемента могло так получить, что несколько верхних уровней перестали содержать какие-либо элементы, тогда необходимо удалить эти уровни (кроме первого), и не забыть вернуть ссылку на начало самого верхнего уровня.

Использование нечестной монеты

Вместо честной монеты с распределением [math]\left\{\dfrac{1}{2}, \ \dfrac{1}{2}\right\}[/math] можно взять в качестве случайного источника нечестную монету с распределением [math]\{p,q\}[/math] (с вероятностью [math]p[/math] выпадает «Орёл»). Тогда математическим ожиданием количества элементов на уровне [math]k[/math] будет [math]n \cdot p^k[/math]. Время поиска будет равно [math]O\left( \dfrac{1}{p} \log_{\frac{1}{p}} {n} \right)[/math] (на [math]i[/math]-ом уровне элементов будет почти в [math]\dfrac{1}{p}[/math] раз больше, чем на [math](i+1)[/math]-ом, значит на каждом уровне пройдём не более [math]\dfrac{1}{p}[/math] элементов, а уровней всего [math]\log_{\frac{1}{p}} {n}[/math]).

Для крайних распределений:

• [math]\{0, 1\}[/math] — [math]O(n)[/math] [math]-[/math] поиск, добавление и удаления элемента, поскольку мы вместо нескольких списком используем по факту всего один список.
• [math]\{1, 0\}[/math] — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным [math]n[/math], значит время поиска будет равным [math]O(n)[/math].

Применение

Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ.

• Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент)
• Проще реализовать, чем сбалансированные деревья или хеш-таблицы
• Следующий элемент достаётся за [math]O(1)[/math]
• Легко модифицировать под различные задачи

Нахождение всех интервалов, покрывающих данную точку

Задача:

Есть [math]q[/math] запросов двух видов: Добавить интервал [math][L, R][/math] Задана точка [math]x[/math]. На каждый запрос второго типа необходимо вывести количество интервалов, которые покрывают данную точку.

Решение данной задачи заключается в том, что когда приходит запрос добавления интервала, то мы добавляем левую и правую границу (если до этого они не были добавлены). Потом идём от левой точки до правой и на пути прибавляем [math]1[/math]. Когда нам приходит запрос второго типа, то рекурсивно спускаемся сверху вниз и суммируем все числа, лежащие на пути между двумя ближайшими вершинами, между которыми находится заданная точка. Очевидно, что оба запроса мы обрабатываем за [math]O(\log{n})[/math], при этом нет никакой необходимости знать запросы заранее.

См. также

• Список
• Рандомизированное бинарное дерево поиска
• Поисковые структуры данных
• Skip quadtree
• Skip graph — структура данных, основанная на списке с пропусками

Источники информации

• Википедия — списки с пропусками
• Wikipedia — skip list
• igoro.com — Skip lists are fascinating
• ticki.github.io — Skip Lists: Done Right
• Eric N. Hanson — A Data Structure for Finding All Intervals That Overlap a Point стр. 155-164