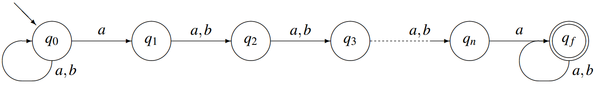Двусторонний детерминированный конечный автомат

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Определение:

Двусторонний детерминированный конечный автомат (2ДКА) (англ. Two-way deterministic finite automaton (2DFA)) — набор из восьми элементов [math]M = \langle \Sigma , Q, L, R, s, t, r, \delta \rangle[/math], где [math]\Sigma[/math] — алфавит, [math]Q[/math] — множество состояний, [math]L \notin \Sigma[/math] — левый маркер конца строки (англ. left endmarker), [math]R \notin \Sigma[/math] — правый маркер конца строки (англ. right endmarker), [math]s \in Q[/math] — начальное (стартовое) состояние, [math]t \in Q[/math] — допускающее состояние, [math]r \in Q[/math] — отвергающее состояние, [math]\delta : Q \times \{\Sigma \cup \{L, R\}\} \to Q \times \{left, right\}[/math] — функция переходов.

Также должны быть удовлетворены следующие условия:

[math]\forall q \in Q[/math]

• [math]\delta(q, L) = (u, right)[/math] для некоторого [math]u \in Q[/math],
• [math]\delta(q, R) = (v, left)[/math] для некоторого [math]v \in Q[/math],

и [math]\forall b \in \Sigma \cup \{L\}[/math]

• [math]\delta(t, b) = (t, right)[/math],
• [math]\delta(r, b) = (r, right)[/math],
• [math]\delta(t, R) = (t, left)[/math],
• [math]\delta(r, R) = (r, left)[/math].

Регулярность языка

Теорема:

Классы языков ДКА и 2ДКА совпадают.

Доказательство:

[math]\triangleright[/math]

Рассмотрим длинную входную строку [math]w_1[/math] и разобьем на две подстроки [math]w_1=xz[/math]. Будем считать, что [math]w_1 = a_1 a_2 a_3 \dots a_n[/math]. Пусть [math]a_0 = L[/math] и [math]a_{n+1}=R[/math]. Так как у нас наш автомат может производить чтение в любом направлении, то граница [math]x[/math] и [math]z[/math] может быть пересечена несколько раз. Каждый раз, когда автомат пересекает границу справа налево (то есть из [math]z[/math] в [math]x[/math]), он выходит из [math]z[/math] в состояние [math]q[/math]. Когда пересечение происходит снова слева направо (если оно вообще происходит), то автомат выходит из [math]x[/math] в состояние [math]p[/math]. Теперь, если 2ДКА перейдет в [math]x[/math] в состояние [math]q[/math] заново, то он снова может появиться в состоянии [math]p[/math]. Более того, состояние [math]p[/math] зависит исключительно от [math]q[/math] и [math]x[/math]. Обозначим такое отношение через [math]T_x(q) = p[/math]. Мы может записать все такие отношения в виде конечной таблицы [math]T_x : Q \cup \{d\} \to Q \cup \{h\}[/math], где [math]Q[/math] — множество состояний 2ДКА, а [math]d[/math] и [math]h[/math] будут описаны ниже. На входной строке [math]xz[/math] 2ДКА начнет чтение с левого маркера конца строки. В процессе работы автомата позиция чтения будет меняться. В конце концов это позиция пересечет слева направо границу между [math]x[/math] и [math]z[/math]. В первый раз это произойдет в каком-нибудь состоянии, которое будем называть [math]T_x(d)[/math] (для этого мы и выделили [math]d[/math]). Так же автомат может никогда не выйти из [math]x[/math]. В таком случае мы запишем [math]T_x(d) = h[/math]. Состояние [math]T_x(d)[/math] дает немного информации о [math]x[/math], но только конечное количество, поскольку существует только конечное количество вариантов для [math]T_x(d)[/math]. Отметим, что [math]T_x(d)[/math] зависит только от [math]x[/math] и не зависит от [math]z[/math]. Если на вход подавалась бы строка [math]xw[/math] вместо [math]xz[/math], то в таком случае при пересечении границы из [math]x[/math] в [math]w[/math] автомат также был бы в состоянии [math]T_x(d)[/math], потому что его значение до того момента определялось только [math]x[/math] и до тех пор все, что находится справа от границы никак не влияет. Если [math]T_x(d) = h[/math], то 2ДКА в бесконечном цикле внутри [math]x[/math], и он никогда не допустит и не отвергнет входную строку. Предположим, что 2ДКА переходит из [math]x[/math] в [math]z[/math] и спустя время переходит обратно в состояние [math]q[/math]. Если это происходит, то потом: либо снова произойдет переход из [math]x[/math] в некоторое состояние [math]p[/math]. В таком случае мы определим [math]T_x(q)=p[/math]. либо никогда не перейдет. В таком случае [math]T_x(q) = h[/math]. Ещё раз отметим, что [math]T_x(q)[/math] зависит только от [math]x[/math] и [math]q[/math] и не зависит от [math]z[/math]. Если автомат переходит в [math]x[/math] справа в состояние [math]q[/math], то тогда он появится заново в состоянии [math]T_x(q)[/math] (или никогда не перейдет, если [math]T_x(q) = h[/math]), потому что автомат детерминированный, и его поведение полностью определяется [math]x[/math] и состоянием, в которое он вошел. Если мы запишем [math]T_x(q)[/math] для каждого состояния [math]q[/math] вместе с [math]T_x(d)[/math], это даст нам всю информацию о [math]x[/math], которую можно перенести через границу между [math]x[/math] и [math]z[/math]. Все это позволит узнать [math]T_x(d)[/math] сразу после пересечения границы, а также посмотреть значения [math]T_x(q)[/math]. Если [math]y[/math] — другая строка, такая что [math]T_y=T_x[/math], то тогда [math]x[/math] и [math]y[/math] будут неразличимы. Заметим, что у нас конечное число возможных таблиц [math]T_x : Q \cup \{d\} \to Q \cup \{h\}[/math], а именно [math](k+1)^{k+1}[/math], где [math]k[/math] — размер множества [math]Q[/math]. Таким образом, у нас конечное количество информации о [math]x[/math], которое мы может перенести через границу справа от [math]x[/math], и которое закодировано у нас в таблицe [math]T_x[/math]. Отметим также, что если [math]T_x=T_y[/math] и автомат допускает строку [math]xz[/math], то тогда он допускает и строку [math]yz[/math], потому что последовательность состояний, перенесенных через границу [math]x[/math] и [math]z[/math] (либо [math]y[/math] и [math]z[/math]) в любом направлении, полностью определяется таблицами [math]T_x=T_y[/math] и строкой [math]z[/math]. Чтобы допустить строку [math]xz[/math], автомат должен в какой-то момент прочитать правый маркер конца строки, находясь в допускающем состоянии [math]t[/math]. Теперь мы может использовать теорему Майхилла-Нероуда, чтобы показать, что язык [math]L(M)[/math] нашего автомата [math]M[/math] регулярный. [math]T_x = T_y \Rightarrow \forall z (M\ \text{accepts}\ xz \Leftrightarrow M\ \text{accepts}\ yz)[/math] [math] \Leftrightarrow \forall z (xz \in L(M)[/math] [math] \Leftrightarrow yz \in L(M)) \Leftrightarrow x \equiv_{L(M)} y[/math], где [math]\equiv_{L(M)}[/math] — отношение эквивалентности на множестве слов в алфавите. Таким образом, если 2 строки имеют одинаковые таблицы, то тогда они эквивалентны отношением [math]\equiv_{L(M)}[/math]. Поскольку у нас только конечное число таблиц, отношение [math]\equiv_{L(M)}[/math] имеет только конечное количество классов эквивалентности, самое большее один для каждой таблицы. Следовательно, по теореме Майхилла-Нероуда, [math]L(M)[/math] — регулярный язык, что согласно теореме Клини, совпадает с классом и автоматных языков, ч.т.д.

[math]\triangleleft[/math]

Пример

Рассмотрим следующий язык [math]L_n = (a+b)^∗a(a+b)^{n-1}a(a+b)^∗[/math] при [math]\forall n \gt 0[/math].

Он может быть легко распознан с помощью следующего недетерминированного конечного автомата.

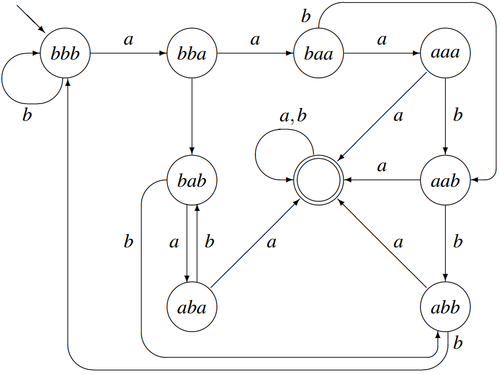
Теперь построим на его основе ДКА. Мы можем построить автомат [math]A_n[/math], который запоминает последние [math]n[/math] входных символов. Следовательно, когда мы находимся в состоянии, соответствующему подстроке [math]\sigma_1 \sigma_2 \dots \sigma_n[/math], и читаем очередной символ [math]\gamma[/math], то мы переходим в состояние, которому уже будет соответствовать подстрока [math]\sigma_2 \sigma_3 \dots \sigma_n \gamma[/math]. Однако, в случае [math]\sigma_1 = \gamma = a[/math] автомат переходит в допускающее состояние, где в цикле может переходить на любому символу. Следует отметить, что такая стратегия строит ДКА c [math]2^n + 1[/math] состояниями. Ниже представлен автомат [math]A_3[/math], который распознает язык [math]L_3[/math].

Покажем, что построенные таким образом автоматы будут минимальными.

• Каждые две попарно различных строки [math]x[/math] и [math]y[/math] длины [math]n[/math] различимы. Чтобы доказать это, достаточно рассмотреть строку [math]b^{i-1}a[/math], где [math]i : 1 \leqslant i \leqslant n[/math] — самая левая позиция символа, в которой начинают различаться строки [math]x[/math] и [math]y[/math], и проверить, что ровно одна строка [math]xb^{i-1}a[/math] или [math]yb^{i-1}a[/math] принадлежит [math]L_n[/math].
• Каждая строка длины [math]n[/math] не принадлежит [math]L_n[/math] и, следовательно, различима со строкой [math]a^{n+1}[/math], которая принадлежит [math]L_n[/math].
• Таким образом, [math]2^n + 1[/math] строк в [math]\Sigma^n \cup \{a^{n+1}\}[/math] являются попарно различимыми для [math]L_n[/math]. Как следствие, [math]2^n + 1[/math] — минимальное количество состояний для ДКА, который способен распознать язык [math]L_n[/math].

Чтобы определить, что строка [math]w=c_1 \dots c_n[/math] принадлежит языку [math]L_n[/math], нужно для [math]\forall i = 1, \dots, |w|-n[/math] проверить, что [math]c_i=c_{i+n}=a[/math]. Строка будет допустимой, если условие сработает хотя бы для одного [math]i[/math]. Этот алгоритм может быть просто реализован с помощью 2ДКА. Будем для каждого [math]i[/math] двигаться на [math]n[/math] позиций вперед, а потом на [math]n-1[/math] позиций назад до позиции [math]i+1[/math]. Кроме того, при движении с позиции [math]i[/math] до [math]i+n[/math] автомат должен помнить сохраняется ли условие [math]c_i=a[/math]. Такой подход требует [math]O(n)[/math] состояний.

См. также

• Локальные автоматы
• Теорема Клини (совпадение классов автоматных и регулярных языков)

Источники информации

• Wikipedia — Two-way deterministic finite automaton
• Википедия — Теорема Майхилла-Нероуда
• Giovanni Pighizzini, Two-Way Finite Automata: Old and Recent Results
• Cornell University, Two-Way Finite Automata
• Liat Peterfreund, Two-way finite automata & pebble automata