Описание
| Определение: |
Граф Майхилла [math]G[/math] (над алфавитом [math]\Sigma[/math]) (англ. Myhill graph) — ориентированный граф, удовлетворяющий свойствам:
- Для каждой упорядоченной пары вершин [math]v[/math] и [math]u[/math] существует только одно ребро из [math]v[/math] в [math]u[/math].
- Некоторые вершины обозначены начальными, а некоторые — конечными. Ребро может одновременно быть начальным и конечным.
- Вершины обозначены различными символами из конечного алфавита [math]\Sigma[/math], то есть мы можем обращаться к вершине по ее символу.
|
Пусть [math]G[/math] — граф Майхилла над алфавитом [math]\Sigma[/math].
Символ [math]c \in \Sigma[/math] назовем разрешенным, если им помечена вершина, являющая одновременно начальной и конечной.
Не пустая строка [math]c_1c_2 \ldots c_n[/math] из [math]\Sigma^*[/math] длиной не менее двух символов, называется разрешенной, если символом [math]c_1[/math] отмечена стартовая вершина, а символом [math]c_n[/math] — конечная, и для всех [math]1 \leqslant i \leqslant n - 1[/math] в [math]G[/math] существует ребро [math](c_i, c_{i+1})[/math].
Язык [math]L(G)[/math], распознаваемый графом Майхилла, состоит из всех разрешенных строк из [math]\Sigma^+[/math].
Покажем, что графы Майхилла могут быть представлены в виде автоматов.
Пусть [math]\mathcal{A} = (S, \Sigma, i, \delta, T)[/math] — ДКА.
| Определение: |
| Автомат [math]\mathcal{A}[/math] называется локальным (англ. local automaton, Glushkov automaton), если для любого [math]c[/math] из [math]\Sigma[/math] множество [math]\{\delta(s, c) \mid s \in S\}[/math] содержит не более одного элемента. |
| Определение: |
| Локальный автомат [math]\mathcal{A}[/math] называется стандартным локальным автоматом (англ. standard local automation), если в нем нет перехода в начальное состояние. |
Таким образом, автомат является локальным, если для каждого [math]c[/math] из [math]\Sigma[/math] нет переходов, отмеченных [math]c[/math], или если все они ведут в одно состояние.
Покажем, что граф Майхилла может быть преобразован в стандартный локальный автомат таким образом, что распознаваемый им язык не изменится.
| Теорема: |
Язык распознается графом Майхилла тогда и только тогда, когда он распознается стандартным локальным автоматом, стартовое состояние которого не является терминальным. |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math]\Rightarrow[/math]
- Пусть [math]G[/math] — граф Майхилла.
- Построим автомат [math]\mathcal{A}[/math] следующим образом:
- Добавим вершину [math]i[/math] в [math]G[/math] с ребрами от [math]i[/math] к каждой стартовой вершине [math]G[/math]; отметим вершину [math]i[/math] как стартовое состояние.
- Отметим конечные вершины как терминальные состояния.
- Отметим каждое ребро результирующего ориентированного графа символом, стоящим в вершине, на которою оно указывает.
- Переходы преобразуются следующим образом:
- По построению стартовое состояние не является терминальным.
- Покажем, что полученный автомат конечен.
- Ребра, выходящие из стартового состояния обозначены различными символами, потому что они указывают на вершины, которые, по свойству 3, были отмечены различными символами в исходном автомате.
- Если мы рассмотрим любое другое состояние [math] s [/math], то два перехода из [math] s [/math] могут иметь одинаковые метки только в том случае, если в [math]G[/math] оба ориентированных ребра идут в одну и ту же вершину. Но этого не может быть по свойству 1.
- То есть [math]\mathcal{A}[/math] — ДКА. По построению он является стандартным локальным автоматом.
- Теперь просто проверить, что [math]L(\mathcal{A}) = L(G) [/math].
[math] \Leftarrow [/math]
- Пусть [math] \mathcal{A} = (S, \Sigma, i, \delta, T) [/math] — стандартный локальный автомат, стартовое состояние которого не является терминальным.
- Построим по нему граф Майхилла следующим образом:
- Отметим все состояния [math] \mathcal{A} [/math], кроме стартового, [math] input [/math] символами, стоящими на ребрах, входящих в эти состояния.
- Сотрем все метки на ребрах [math] \mathcal{A} [/math].
- Отметим все состояния [math] s [/math] как начальные вершины, если существует переход из [math] i [/math] в [math] s [/math]
- Отметим все терминальные состояния как конечные вершины.
- Удалим вершину [math] i [/math] и все ребра, исходящие из нее.
- Назовем полученный граф [math] G [/math] — он будет графом Майхилла по построению. Легко проверить, что [math] L(G) = L(\mathcal{A}) [/math].
|
| [math]\triangleleft[/math] |
Пример
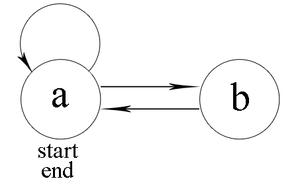
Граф Майхилла, изображенный на рисунке 1 может быть использован для распознавания строк над алфавитом [math]\Sigma = \{a, b\}[/math]. По определению, язык, распознаваемый данным графом, состоит из непустых строк, начинающихся и заканчивающихся на [math]a[/math].
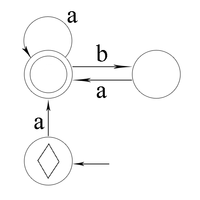
Недетерминированный автомат на рисунке 2 является локальным автоматом и распознает тот же самый язык.
Локальный язык
Рассмотрим язык, распознаваемый стандартным локальным автоматом.
| Определение: |
Язык [math]L \subseteq A^*[/math] называется локальным языком (англ. local language), если [math]L \setminus \varepsilon[/math] может быть описан следующим образом:
[math]\exists P, S \subseteq A, N \subseteq A^2: L \setminus \varepsilon = (P A^* \cap A^* S) \setminus A^* N A^*[/math]. |
Другими словами, непустое слово принадлежит локальному языку, если оно начинается с символа из [math]P[/math], оканчивается на символ из [math]S[/math] и не содержит пары символов из множества [math]N[/math].
Пусть [math]L = (P A^* \cap A^* S) \setminus A^* N A^*[/math] — локальный язык. Определим автомат [math]\mathcal{A}[/math] следующим образом:
- набор состояний [math]Q = A \cup \{ \varepsilon \}[/math],
- начальное состояние [math]\varepsilon[/math],
- терминальные состояния [math]S[/math],
- [math]\delta(\varepsilon, a) = a[/math] если [math]a \in P[/math] и [math]\delta(a, b) = b[/math] если [math]ab \not\in N[/math].
Если [math]L[/math] содержит пустую строку, то множество терминальных состояний [math]\mathcal{A}[/math] — [math]S \cup \{ \varepsilon \}[/math].
| Утверждение: |
Определенный таким образом автомат [math]\mathcal{A}[/math] — стандартный локальный автомат, распознающий [math]L[/math]. |
| [math]\triangleright[/math] |
|
Автомат является локальным поскольку для каждого состояния [math]s[/math] и любого символа [math]a[/math] [math]\delta(s, a)[/math] либо неопределена либо равна [math]a[/math]. По построению автомат является стандартным. Покажем, что [math]L(\mathcal{A}) = L[/math].
Пусть [math]x = a_1 \ldots a_n \in L(\mathcal{A})[/math]. Тогда в автомате существует путь:
- [math]\varepsilon \xrightarrow{a_1} a_1 \xrightarrow{a_2} a_2 \ldots a_{n-1} \xrightarrow{a_n} a_n[/math].
Здесь [math]a_n[/math] — терминальное состояние, [math]a_n \in S[/math]. Переход из [math]\varepsilon[/math] в [math]a_1[/math] определен, поэтому [math]a_1 \in P[/math]. Для каждого [math]j: 1 \leqslant j \leqslant n - 1[/math] факт, что переход [math]a_j \rightarrow a_{j+1}[/math] существует, означает что [math]a_j a_{j+1} \not \in N[/math]. Следовательно, [math]x \in L[/math].
Пусть [math]x = a_1 \ldots a_n \in L[/math]. Тогда [math]a_1 \in P[/math], [math]a_n \in S[/math] и для каждого [math]j[/math] [math]a_j a_{j+1} \not \in N[/math]. Следовательно в автомате существует путь из начального состояния в терминальное:
- [math]\varepsilon \xrightarrow{a_1} a_1 \xrightarrow{a_2} a_2 \ldots a_{n-1} \xrightarrow{a_n} a_n[/math].
Следовательно, [math]x \in L(\mathcal{A})[/math]. |
| [math]\triangleleft[/math] |
| Утверждение: |
Язык, распознаваемый локальным автоматом, является локальным. |
Алгоритм Глушкова
Описание
Дано регулярное выражение [math]e[/math]. Алгоритм Глушкова строит недетерминированный автомат, который распознает язык [math]L(e)[/math], распознаваемый [math]e[/math]. Построение происходит в несколько шагов:
- Линеаризация регулярного выражения. Каждый символ из алфавита, содержащийся в регулярном выражении, переименовывается таким образом, что каждый символ содержится в новом регулярном выражении не более одного раза. Пусть [math]A[/math] — исходный алфавит, [math]B[/math] — новый алфавит.
- Вычисление множеств [math]P(e'), S(e'), N(e')[/math], где [math]e'[/math] — линеаризованное регулярное выражение. [math]P(e')[/math] — множество символов, с которых начинается слово из [math]L(e')[/math]. [math]S(e')[/math] — множество символов, на которые оканчивается слово из [math]L(e')[/math] и [math]N(e')[/math] — множество пар символов, которые встречаются в слове из [math]L(e')[/math]. Более формально:
[math]P(e')=\{a\in B\mid aB^*\cap L(e')\ne\emptyset\}[/math],
[math]S(e')=\{a\in B\mid B^*a\cap L(e')\ne\emptyset\}[/math],
[math]N(e')=\{u\in B^2\mid B^*uB^*\cap L(e')\ne\emptyset\}[/math].
- Вычисление множества [math]\Lambda(e')[/math] такого что [math]\Lambda(e')=\{\varepsilon\}\cap L(e')[/math].
- Вычисление локального языка с заданными множествами и построение по нему автомата.
- Делинеаризация, переименование каждого символа из [math]B[/math] в соответствующий ему символ из [math]A[/math].
Пример работы
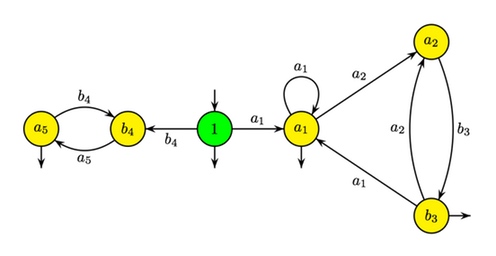
Автомат, построенный в ходе работы алгоритма Глушкова
Рассмотрим регулярное выражение [math]e = (a(ab)^*)^* + (ba)^*[/math]:
- Линеаризуем его путем добавления индекса к каждому символу:
- [math]e'=(a_1(a_2b_3)^*)^*+(b_4a_5)^*[/math].
- Составим множества [math]P[/math], [math]S[/math], и [math]N[/math]:
- [math]P(e')=\{a_1,b_4\}[/math],
- [math]S(e')=\{a_1,b_3,a_5\}[/math],
- [math]N(e')=\{a_1a_2, a_1a_1, a_2b_3, b_3a_1,b_3a_2,b_4a_5,a_5b_4\}[/math].
Так как пустое слово принадлежит языку, то [math]\Lambda(e')=\{\varepsilon\}[/math].
- Автомат локального языка [math]L'=P'B^*\cap B^*S'\setminus B^*(B^2\setminus N')B^*[/math] содержит начальное состояние, обозначенное как [math]1[/math], и состояния для каждого из пяти символов алфавита [math]B=\{a_1, a_2, b_3, b_4, a_5\}[/math].
В построенном автомате существует переход из [math]1[/math] (соответствующего пустой строке) в два состояния из [math]P'[/math], переход из [math]a[/math] в [math]b[/math] если [math]ab \in N'[/math], три состояния [math]S'[/math] терминальные (как и состояние [math]1[/math]).
- Получим автомат для [math]L(e)[/math], удалив индексы, добавленные на первом этапе.
См. также
Источники информации