Турниры — различия между версиями
Rgolchin (обсуждение | вклад) (→Транзитивность) |
м (rollbackEdits.php mass rollback) |
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:28, 4 сентября 2022
| Определение: |
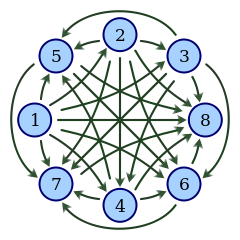
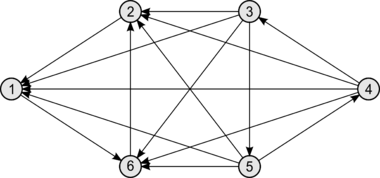
| Турнир (англ. Tournament) — ориентированный граф, между любой парой различных вершин которого есть ровно одно ориентированное ребро. |
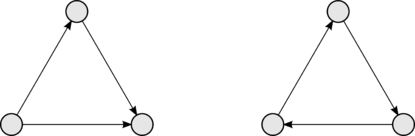
Турниром из вершин можно изобразить исход игры между людьми, где каждый играет с каждым. Тогда ребро будет ориентировано от выигравшего человека к проигравшему.
Содержание
Свойства турниров
Оценка количества турниров в графе
Если в турнире опустить ориентацию ребер, то мы получим полный граф. А так как существует два варианта ориентации каждого ребра, то количество турниров в графе из вершин равно .
Транзитивность
Турнир, в котором , называется транзитивным. В транзитивном турнире вершины могут быть полностью упорядочены в порядке достижимости.
| Теорема: |
Пусть — турнир, . Тогда следующие утверждения эквивалентны:
|
| Доказательство: |
|
Пусть существует цикл длины Однако по транзитивности должно существовать ребро , т.е. между есть противоположно направленных ребра, что невозможно по определению турнира. Пусть в графе содержится цикл длины . Это не может быть цикл длины (противоречит определению турнира). Обозначим его вершины в порядке обхода . Заметим, что т.к. нет циклов длины , выполнена транзитивность (в противном случае существовали бы ребра ). Докажем по индукции, что существует ребро База индукции : (по транзитивности). Переход индукции Пусть доказано для всех , что , также известно, что , тогда по транзитивности . Таким образом, в транзитивном турнире содержится цикл длины — противоречие (см. предыдущий пункт). Обозначим множество значений степеней исхода как . Докажем индукцией по . База индукции : верно, т.к. есть одна вершина степени Переход индукции Пусть доказано для . В ациклическом графе существует сток . Рассмотрим граф . . Т.к. из каждой ведет одно ребро в , . Для степеней захода можно доказать аналогично, рассмотрев исток вместо стока. По теореме Редеи-Камиона, в любом турнире есть гамильтонов путь, докажем индукцией по , что этот путь единственный. База индукции : верно, путь из одной вершины. Переход индукции Рассмотрим вершину . Она будет первой в гамильтоновом пути (иначе мы в нее не зайдем). Рассмотрим граф . Т.к. была соединена со всеми его вершинами, их степени меньше на соответствующих степеней в исходном турнире, значит , следовательно в существует единственный гамильтонов путь (по предположению). Пусть существуют гамильтонова пути, начинающиеся на , но тогда существуют 2 пути в — противоречие. Пусть — единственный гамильтонов путь. Пусть найдется — наименьший индекс такой, что в вершину идет ребро из вершины с большим индексом, а — вершина с наибольшим индексом, из которой ребро ведет в . Возможно несколько случаев:
Замечание Может достигаться равенство , в этом случае нужно исключить из пути последовательных вхождения . Во всех случаях получаем противоречие с единственностью гамильтонова пути, значит не существует такого , т.е . Значит . |
Теория Рамсея
Транзитивные турниры играют существенную роль в теории Рамсея, изучающей условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. В частности, любой турнир с вершинами содержит транзитивный подтурнир с вершинами. Для его построения выберем любую вершину как часть этого подтурнира и построим подтурнир рекурсивно на множестве либо входящих соседей вершины , либо на множестве исходящих соседей, в зависимости от того, какое множество больше.
Конденсация
| Утверждение: |
Конденсация любого турнира является транзитивным турниром. |
| Рассмотрим компоненты сильной связности , найдутся , либо , значит в конденсации есть либо ребро , либо . Т.к. мы рассмотрели произвольную пару вершин конденсации турнира, она является турниром. Конденсация любого орграфа ациклична, а по доказанной теореме, это означает, что она транзитивна. |
Таким образом, даже если турнир не является транзитивным, сильно связанные компоненты турнира могут быть вполне упорядочены. В самом деле, по теореме, в турнире существует гамильтонов путь, значит вершины могут быть упорядочены по своим позициям в этом пути.
Сильно связные турниры
| Определение: |
| Турнир называется сильно связным, если из любой вершины существуют пути до всех других. |
| Определение: |
| Турнир называется гамильтоновым, если он содержит гамильтонов цикл. |
Не все турниры гамильтоновы. Определение не исключает существование вершины с или равной нулю — в первую нельзя войти, а из второй — выйти. Однако отсутствие таких вершин не означает, что турнир гамильтонов (пример — на рисунке справа).
Теорема Редеи-Камиона устанавливает два следующих факта:
- Все турниры полугамильтоновы.
- Турнир гамильтонов тогда и только тогда, когда он сильно связен.
См. также
Источники информации
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — ISBN 5-93972-076-5
- Wikipedia — Турнир
- [1]