Сортирующие сети — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 38 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| + | == Определение == | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | '''Сортирующая сеть''' (англ. ''Sorting network'') — метод сортировки, основанный только на сравнениях данных. Схематически изображается в виде параллельных прямых (проводов), соединенных вертикальными линиями (сравнивающими устройствами). Особенность сети сортировки в том, что сравнения выполняются независимо от предыдущих. Кроме того, сравнения могут выполняться одновременно. | |
}} | }} | ||
| − | |||
| + | {| cellpadding="3" | ||
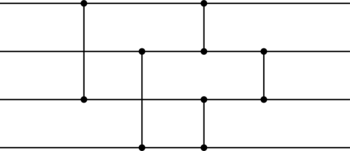
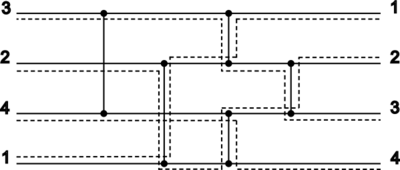
| + | | || [[Файл:Network.png|thumb|right|350px|Схематическое изображение сортирующей сети для последовательности из 4 чисел. Глубина сети: 4. Размер сети: 5 ]] || [[Файл:Sort1.png|thumb|right|400px|Процесс сортировки числовой последовательности (3, 2, 4, 1)]] | ||
| + | |} | ||
| + | == Компараторы (сравнивающие устройства) == | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Компаратор''' (англ. ''Comparator'') — устройство, подключенное к двум проводам, которое упорядочивает текущие значения на проводах. | ||
| + | }} | ||
| + | {| cellpadding="3" | ||
| + | | [[Файл:Comp1.png|thumb|500px|Компаратор, подключенный к проводам <tex>i, j</tex>. Входные данные: <tex>x, y</tex>. Выходные данные: <tex>\min(x, y), \max(x, y)</tex>.]] | ||
| + | |} | ||
| + | Обычно компараторы меньшее значение передают на провод с меньшим номером, но бывают и направленные компараторы, у которых указано направление перемещения. | ||
| − | |||
{{Определение | {{Определение | ||
| − | |definition = | + | |definition = |
| − | ''' | + | '''K-компаратор''' (англ. ''K-comparator'') — устройство, упорядочивающее значения на <tex>k</tex> проводах. |
}} | }} | ||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | ''' | + | Пусть глубина входного провода сети равна нулю. Если глубины входных проводов компаратора равны <tex>x</tex> и <tex>y</tex>, то глубина его выходных проводов равна <tex>\max(x, y) + 1 </tex>. '''Глубина компаратора''' (англ. ''Depth of comparator'') — величина, равная глубине его выходных проводов. |
}} | }} | ||
| − | + | Компараторы можно располагать на одной глубине, если они подключены к разным проводам. В этом случае сравнения будут выполняться параллельно. | |
| + | |||
== Сети == | == Сети == | ||
| + | |||
| + | Введем ряд определений, характеризующих сеть компараторов: | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Слой сети''' (англ. ''layer'') — множество компараторов, имеющих одинаковую глубину. | ||
| + | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | ''' | + | '''Глубина сети''' (англ. ''depth'') — количество слоев в сети. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | ''' | + | '''Размер сети''' (англ. ''size'') — количество компараторов в сети. |
}} | }} | ||
| + | |||
| + | Для того, чтобы сортирующая сеть для <tex>n</tex> входов была корректна, она должна правильно сортировать все <tex>n!</tex> перестановок <tex>n</tex> различных чисел. Также можно сформулировать более сильное утверждение: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Сеть является сортирующей тогда и только тогда, когда она сортирует | + | Сеть компараторов с <tex>n</tex> входами является сортирующей тогда и только тогда, когда она сортирует <tex>2^n</tex> различных последовательностей из 0 и 1. |
}} | }} | ||
| − | + | {{main | 0-1 принцип}} | |
| − | |||
== См.также == | == См.также == | ||
| − | [[Сортирующие сети для квадратичных сортировок]] | + | *[[Сортирующие сети для квадратичных сортировок]] |
| − | + | *[[0-1 принцип]] | |
| − | [[0-1 принцип]] | + | *[[Сеть Бетчера]] |
| − | |||
| − | [[Сеть Бетчера]] | ||
| − | |||
| − | == Источники == | + | == Источники информации== |
| − | * Кормен | + | * [[wikipedia:Sorting_network | Wikipedia {{---}} Sorting network]] |
| − | * | + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 799 — 805. — ISBN 5-8489-0857-4 |
| + | * Дональд Э. Кнут Искусство программирования. Том 3. Сортировка и поиск — 2-е изд. — М.: «Вильямс», 2012. — с. 238 — 242. — ISBN 0-201-89685-0 | ||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Сортирующие сети]] | [[Категория: Сортирующие сети]] | ||
Текущая версия на 19:33, 4 сентября 2022
Содержание
Определение
| Определение: |
| Сортирующая сеть (англ. Sorting network) — метод сортировки, основанный только на сравнениях данных. Схематически изображается в виде параллельных прямых (проводов), соединенных вертикальными линиями (сравнивающими устройствами). Особенность сети сортировки в том, что сравнения выполняются независимо от предыдущих. Кроме того, сравнения могут выполняться одновременно. |
Компараторы (сравнивающие устройства)
| Определение: |
| Компаратор (англ. Comparator) — устройство, подключенное к двум проводам, которое упорядочивает текущие значения на проводах. |
Обычно компараторы меньшее значение передают на провод с меньшим номером, но бывают и направленные компараторы, у которых указано направление перемещения.
| Определение: |
| K-компаратор (англ. K-comparator) — устройство, упорядочивающее значения на проводах. |
| Определение: |
| Пусть глубина входного провода сети равна нулю. Если глубины входных проводов компаратора равны и , то глубина его выходных проводов равна . Глубина компаратора (англ. Depth of comparator) — величина, равная глубине его выходных проводов. |
Компараторы можно располагать на одной глубине, если они подключены к разным проводам. В этом случае сравнения будут выполняться параллельно.
Сети
Введем ряд определений, характеризующих сеть компараторов:
| Определение: |
| Слой сети (англ. layer) — множество компараторов, имеющих одинаковую глубину. |
| Определение: |
| Глубина сети (англ. depth) — количество слоев в сети. |
| Определение: |
| Размер сети (англ. size) — количество компараторов в сети. |
Для того, чтобы сортирующая сеть для входов была корректна, она должна правильно сортировать все перестановок различных чисел. Также можно сформулировать более сильное утверждение:
| Теорема: |
Сеть компараторов с входами является сортирующей тогда и только тогда, когда она сортирует различных последовательностей из 0 и 1. |
См.также
Источники информации
- Wikipedia — Sorting network
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 799 — 805. — ISBN 5-8489-0857-4
- Дональд Э. Кнут Искусство программирования. Том 3. Сортировка и поиск — 2-е изд. — М.: «Вильямс», 2012. — с. 238 — 242. — ISBN 0-201-89685-0