Сеть Бетчера — различия между версиями
(Отмена правки 60197 участника Alexandra Sannikova (обсуждение)) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 20 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Сеть Бетчера''' (англ. ''Batcher bitonic mergesort'') {{---}} сортирующая сеть размером <tex>O(n \log^2n)</tex> и глубиной <tex>O(\log^2n)</tex>, где <tex>n</tex> {{---}} | + | '''Сеть Бетчера''' (англ. ''Batcher bitonic mergesort'') {{---}} [[Сортирующие сети|сортирующая сеть]] размером <tex>O(n \log^2n)</tex> и глубиной <tex>O(\log^2n)</tex>, где <tex>n</tex> {{---}} число элементов для сортировки. Её авторство принадлежит Кену Бетчеру<ref>[http://en.wikipedia.org/wiki/Ken_Batcher Wikipedia {{---}} Ken Batcher]</ref>. |
В этой статье будет описана сортирующая сеть для случая когда <tex>n</tex> {{---}} степень двойки (<tex>n = 2^k</tex>). | В этой статье будет описана сортирующая сеть для случая когда <tex>n</tex> {{---}} степень двойки (<tex>n = 2^k</tex>). | ||
| Строка 11: | Строка 11: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Нуль-единичные битонические последовательности''' {{---}} кортежи из нулей и единиц вида <tex>0^i1^j0^k</tex> или <tex>1^i0^j1^k</tex> для целых <tex>i,j,k\ | + | '''Нуль-единичные битонические последовательности''' {{---}} кортежи из нулей и единиц вида <tex>0^i1^j0^k</tex> или <tex>1^i0^j1^k</tex> для целых <tex>i,j,k\geqslant0</tex>, где <tex>1^i</tex> или <tex>0^i</tex> обозначает <tex>i</tex> идущих подряд единиц или нулей соответственно.}} |
Приведем несколько примеров нуль-единичной битонической последовательности: <tex>00111000</tex>, <tex>11000111</tex>, <tex>1110</tex>, <tex>1</tex>, <tex>000</tex>. | Приведем несколько примеров нуль-единичной битонической последовательности: <tex>00111000</tex>, <tex>11000111</tex>, <tex>1110</tex>, <tex>1</tex>, <tex>000</tex>. | ||
| Строка 19: | Строка 19: | ||
== Битонический сортировщик == | == Битонический сортировщик == | ||
| − | Построим сеть, которая эффективно сортирует все битонические последовательности {{---}} так называемый '''битонический сортировщик ''(bitonic sorter | + | Построим сеть, которая эффективно сортирует все битонические последовательности {{---}} так называемый '''битонический сортировщик''' (англ. ''bitonic sorter''). |
{| | {| | ||
| | | | ||
=== Полуфильтр === | === Полуфильтр === | ||
| − | Битонический сортировщик представляет собой каскад так называемых '''полуфильтров ''(half-cleaner | + | Битонический сортировщик представляет собой каскад так называемых '''полуфильтров''' (англ. ''half-cleaner''). |
| − | Каждый полуфильтр {{---}} сеть компараторов единичной глубины, в которой <tex>i</tex>-й входной провод сравнивается со входным проводом с номером <tex>\ | + | Каждый полуфильтр {{---}} сеть компараторов единичной глубины, в которой <tex>i</tex>-й входной провод сравнивается со входным проводом с номером <tex>\dfrac{n}{2} + i</tex>, где <tex>i=1,2,\dots,\dfrac{n}{2}</tex> (число входов <tex>n</tex> {{---}} чётное). |
{{Лемма|statement= | {{Лемма|statement= | ||
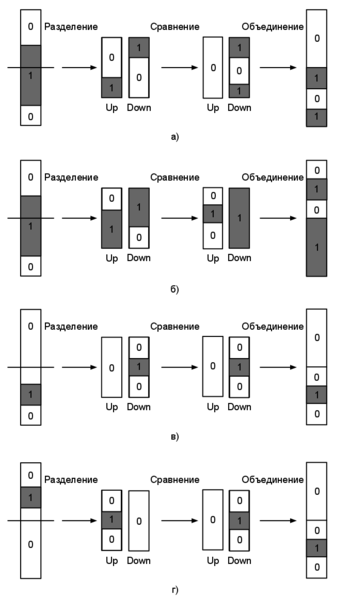
| − | Если на вход в полуфильтр подать битоническую последовательность из нулей и единиц длиной <tex>n</tex>, то на выходе мы получим две битонические последовательности длиной <tex>\ | + | Если на вход в полуфильтр подать битоническую последовательность из нулей и единиц длиной <tex>n</tex>, то на выходе мы получим две битонические последовательности длиной <tex>\dfrac{n}{2}</tex> такие, что каждый элемент из верхней последовательности не превосходит любой элемент из нижней, и что одна из них будет '''однородной''' (англ. ''clean'') {{---}} целиком состоящей либо из нулей, либо из единиц. |
|proof= | |proof= | ||
| − | Для всех <tex>i=1,2, | + | Для всех <tex>i=1,2,\dots,\dfrac{n}{2}</tex> полуфильтр сравнивает провода с номерами <tex>i</tex> и <tex>i+\dfrac{n}{2}</tex>. Без потери общности будем рассматривать входную последовательность вида <tex>0\dots01\dots10\dots0</tex> (для последовательности вида <tex>1\dots10\dots01\dots1</tex> рассуждения аналогичны). В зависимости от того в каком блоке из последовательно расположенных нулей и единиц находится средняя точка <tex>\dfrac{n}{2}</tex> входной последовательности, можно выделить 3 случая, причем один из случаев (когда средняя точка попадает на блок из единиц) можно разбить еще на 2 случая. Все 4 случая разобраны на рисунке справа. Для каждого из них лемма выполняется. |
}} | }} | ||
||[[Файл:Half-Cleaner1.png|262px|right|thumb|Полуфильтр для 8 проводов.]] | ||[[Файл:Half-Cleaner1.png|262px|right|thumb|Полуфильтр для 8 проводов.]] | ||
| Строка 37: | Строка 37: | ||
[[Файл:Half-Cleaner-proof.png|350px|center|thumb|Все случаи попадания битонической последовательности на полуфильтр.]] | [[Файл:Half-Cleaner-proof.png|350px|center|thumb|Все случаи попадания битонической последовательности на полуфильтр.]] | ||
| − | |||
=== Построение битонического сортировщика === | === Построение битонического сортировщика === | ||
| Строка 45: | Строка 44: | ||
Так можно построить сеть для числа входов, являющегося степенью двойки. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна <tex>\log_{2}n</tex>, где <tex>n</tex> {{---}} число входов. | Так можно построить сеть для числа входов, являющегося степенью двойки. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна <tex>\log_{2}n</tex>, где <tex>n</tex> {{---}} число входов. | ||
| − | Количество компараторов равно <tex dpi="150">\frac{n \log_2{n}}{2}</tex>, потому что размер одного полуфильтра на <tex>n</tex> входов {{---}} <tex>\ | + | Количество компараторов равно <tex dpi="150">\frac{n \log_2{n}}{2}</tex>, потому что размер одного полуфильтра на <tex>n</tex> входов {{---}} <tex>\dfrac{n}{2}</tex> компараторов, а в слое битонического сортировщика находится <tex>2^{i-1}</tex> полуфильтров, где <tex>i</tex> {{---}} номер слоя, начиная с единицы. |
== Объединяющая сеть == | == Объединяющая сеть == | ||
| Строка 54: | Строка 53: | ||
Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности: | Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности: | ||
| − | Отсортированная последовательность имеет вид <tex>0^i1^j</tex> для целых <tex>i, j\ | + | Отсортированная последовательность имеет вид <tex>0^i1^j</tex> для целых <tex>i, j\geqslant0</tex>. Запишем две входные последовательности как <tex>0^i1^j</tex> и <tex>0^k1^l</tex>. Если перевернуть вторую последовательность, получится отсортированная по невозрастанию последовательность <tex>1^l0^k</tex>. Если теперь записать первую и перевернутую вторую последовательности подряд, получится битоническая последовательность <tex>0^i1^{j+l}0^k</tex>, которую можно отсортировать в битоническом сортировщике с глубиной <tex>O(\log{n})</tex>. |
| − | Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера <tex>\ | + | Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера <tex>\dfrac{n}{2}</tex>). Поэтому первый полуфильтр будет отличаться от остальных {{---}} он будет соединять <tex>i</tex>-ый провод не с <tex>\dfrac{n}{2} + i</tex>-ым, а с <tex>n-i+1</tex>-ым проводом. Схема объединяющей сети для восьми проводов приведена ниже. |
Глубина и число компараторов в объединяющей сети очевидно те же, что и в битоническом сортировщике. | Глубина и число компараторов в объединяющей сети очевидно те же, что и в битоническом сортировщике. | ||
| Строка 66: | Строка 65: | ||
Теперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию [[сортировка слиянием|сортировки слиянием]]. | Теперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию [[сортировка слиянием|сортировки слиянием]]. | ||
| − | Пусть мы хотим отсортировать <tex>n=2^k</tex> входов, <tex>k</tex> {{---}} целое и <tex>k \ | + | Пусть мы хотим отсортировать <tex>n=2^k</tex> входов, <tex>k</tex> {{---}} целое и <tex>k \geqslant0</tex>. Для этого сначала отсортируем пары проводов, поставив в первом слое компаратор между <tex>i</tex>-ым и <tex>i+1</tex>-ым проводом для нечетных <tex>i < n</tex>. Затем с помощью объединяющих сетей параллельно объединим отсортированные пары проводов в отсортированные четверки. Затем объединим отсортированные четверки в отсортированные восьмерки. И так далее, пока на выходе очередной объединяющей сети не будет <tex>n</tex> проводов. |
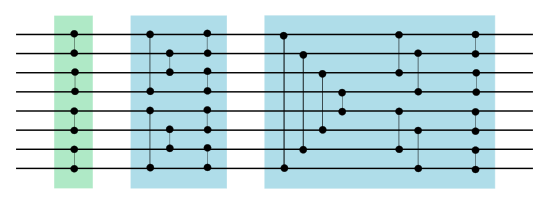
[[Файл:Sorter_8.png|549px|center|thumb|Сортирующая сеть для восьми проводов.]] | [[Файл:Sorter_8.png|549px|center|thumb|Сортирующая сеть для восьми проводов.]] | ||
| Строка 73: | Строка 72: | ||
=== Точные формулы размера и глубины сети === | === Точные формулы размера и глубины сети === | ||
| − | Оценим глубину этой сортирующей сети. Она состоит из <tex>\log_2{n}</tex> слоёв объединяющих сетей и каждый слой имеет глубину, зависящую от его номера. В слое с номером <tex>i</tex> (<tex>1 \ | + | Оценим глубину этой сортирующей сети. Она состоит из <tex>\log_2{n}</tex> слоёв объединяющих сетей и каждый слой имеет глубину, зависящую от его номера. В слое с номером <tex>i</tex> (<tex>1 \leqslant i \leqslant \log_2{n}</tex>) объединяющая сеть имеет глубину <tex>\log_2{2^i}</tex>, потому как объединяет <tex>2^i</tex> проводов. Таким образом глубина всей сортирующей сети в точности равна <tex>\sum\limits^{\log_2{n}}_{i = 1}{\log_2{2^i}} = \sum\limits^{\log_2{n}}_{i = 1}{i} = \dfrac{(1+\log_2{n})\log_2{n}}{2}</tex>. |
| + | |||
| + | Оценим размер сети. В объединяющей сети на <tex>n</tex> входов содержится <tex>\dfrac{n \log_2{n}}{2}</tex> компараторов. Снова просуммируем формулу по числу объединяющих сетей и получим точную оценку <tex>\sum\limits^{\log_2{n}}_{i = 1}{ \dfrac{2^i \log_2{2^i}}{2} } = \sum\limits^{\log_2{n}}_{i = 1}{ 2^{i-1} i} = \dfrac{n \log_{2}^{2}{n} + 2 \log_2{n}}{4}</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Сортирующие сети для квадратичных сортировок]] | ||
| + | * [[Сортировочные сети с особыми свойствами]] | ||
| − | + | ==Примечания== | |
| + | <references /> | ||
==Источники информации== | ==Источники информации== | ||
| − | *[ | + | *[[wikipedia:Bitonic_sorter | Wikipedia {{---}} Bitonic sorter]] |
*Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2005. — С. 808—818. | *Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2005. — С. 808—818. | ||
<!-- TODO: проверить 2007 издание Кормена и написать его --> | <!-- TODO: проверить 2007 издание Кормена и написать его --> | ||
Текущая версия на 19:33, 4 сентября 2022
Сеть Бетчера (англ. Batcher bitonic mergesort) — сортирующая сеть размером и глубиной , где — число элементов для сортировки. Её авторство принадлежит Кену Бетчеру[1].
В этой статье будет описана сортирующая сеть для случая когда — степень двойки ().
Содержание
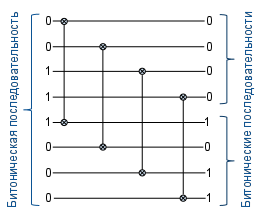
Битоническая последовательность
Сначала введем все необходимые понятия для построения сортирующей сети Бетчера.
| Определение: |
| Битонической последовательностью (англ. bitonic sequence) называется конечный упорядоченный набор (кортеж) из вещественных чисел, в котором они сначала монотонно возрастают, а затем монотонно убывают, или набор, который приводится к такому виду путем циклического сдвига. |
Здесь мы воспользуемся 0-1 принципом и будем рассматривать только нуль-единичные битонические последовательности:
| Определение: |
| Нуль-единичные битонические последовательности — кортежи из нулей и единиц вида или для целых , где или обозначает идущих подряд единиц или нулей соответственно. |
Приведем несколько примеров нуль-единичной битонической последовательности: , , , , .
Далее будет показано, что битоническую последовательность можно легко получить из двух отсортированных, поэтому если мы найдем способ эффективно её сортировать, то сможем столь же эффективно сливать (объединять) две отсортированные последовательности в одну. На этой операции и основывается принцип работы описываемой в этой статье сети сортировки.
Битонический сортировщик
Построим сеть, которая эффективно сортирует все битонические последовательности — так называемый битонический сортировщик (англ. bitonic sorter).
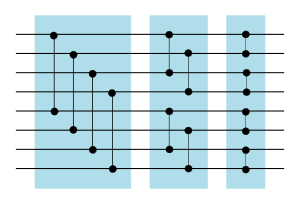
ПолуфильтрБитонический сортировщик представляет собой каскад так называемых полуфильтров (англ. half-cleaner). Каждый полуфильтр — сеть компараторов единичной глубины, в которой -й входной провод сравнивается со входным проводом с номером , где (число входов — чётное).
|
Построение битонического сортировщика
Теперь используем полуфильтры для сортировки битонических последовательностей. Как только что было доказано, один полуфильтр разделяет битоническую последовательность на две равные части, одна из которых однородна, а другая сама по себе является битонической последовательностью, причем части расположены в правильном порядке. Тогда мы можем каждую часть снова отправить в полуфильтр вдвое меньшего размера, чем предыдущий. Затем, если нужно, четыре получившихся части снова отправить в полуфильтры и так далее, пока количество проводов в одной части больше .
Так можно построить сеть для числа входов, являющегося степенью двойки. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна , где — число входов. Количество компараторов равно , потому что размер одного полуфильтра на входов — компараторов, а в слое битонического сортировщика находится полуфильтров, где — номер слоя, начиная с единицы.
Объединяющая сеть
Битонический сортировщик находит своё применение в конструкции так называемой объединяющей сети.
| Определение: |
| Объединяющая сеть (англ. merger) — сеть компараторов, объединяющая две отсортированные входные последовательности в одну отсортированную выходную последовательность. |
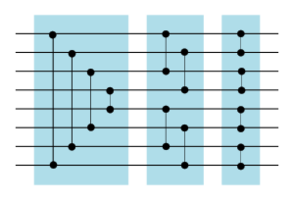
Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности:
Отсортированная последовательность имеет вид для целых . Запишем две входные последовательности как и . Если перевернуть вторую последовательность, получится отсортированная по невозрастанию последовательность . Если теперь записать первую и перевернутую вторую последовательности подряд, получится битоническая последовательность , которую можно отсортировать в битоническом сортировщике с глубиной .
Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера ). Поэтому первый полуфильтр будет отличаться от остальных — он будет соединять -ый провод не с -ым, а с -ым проводом. Схема объединяющей сети для восьми проводов приведена ниже.
Глубина и число компараторов в объединяющей сети очевидно те же, что и в битоническом сортировщике.
Сортирующая сеть
Построение
Теперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию сортировки слиянием.
Пусть мы хотим отсортировать входов, — целое и . Для этого сначала отсортируем пары проводов, поставив в первом слое компаратор между -ым и -ым проводом для нечетных . Затем с помощью объединяющих сетей параллельно объединим отсортированные пары проводов в отсортированные четверки. Затем объединим отсортированные четверки в отсортированные восьмерки. И так далее, пока на выходе очередной объединяющей сети не будет проводов.
Так мы построили сеть, сортирующую любую последовательность из нулей и единиц. А это означает, согласно 0-1 принципу, что она будет сортировать и любой набор чисел.
Точные формулы размера и глубины сети
Оценим глубину этой сортирующей сети. Она состоит из слоёв объединяющих сетей и каждый слой имеет глубину, зависящую от его номера. В слое с номером () объединяющая сеть имеет глубину , потому как объединяет проводов. Таким образом глубина всей сортирующей сети в точности равна .
Оценим размер сети. В объединяющей сети на входов содержится компараторов. Снова просуммируем формулу по числу объединяющих сетей и получим точную оценку .
См. также
Примечания
Источники информации
- Wikipedia — Bitonic sorter
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2005. — С. 808—818.