Троичный сумматор — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
м (rollbackEdits.php mass rollback)
 
(не показаны 4 промежуточные версии 2 участников)
Строка 1: Строка 1:
 
В [[Троичная_логика |троичной логике]] "лжи" и "истине" соответствует <tex>-</tex> и <tex>+</tex>. Третьему состоянию соответствует <tex>0</tex>.
 
В [[Троичная_логика |троичной логике]] "лжи" и "истине" соответствует <tex>-</tex> и <tex>+</tex>. Третьему состоянию соответствует <tex>0</tex>.
  
−
Мы будем рассматривать простую троичную [[Реализация_булевой_функции_схемой_из_функциональных_элементов |функциональную схему]] — троичный [[Сумматор|сумматор]]. Поэтому, вместо обозначений <tex>\{-, 0, +\}</tex>, мы используем <tex>\{0, 1, 2\}</tex> (несимметричная троичная система счисления).
+
Мы будем рассматривать простую троичную [[Реализация_булевой_функции_схемой_из_функциональных_элементов |функциональную схему]] — троичный [[Сумматор|сумматор]]. В нём используются такие обозначения: <tex>\{0, 1, 2\}</tex> (несимметричная троичная система счисления).
  
 
== Составные части полусумматора ==
 
== Составные части полусумматора ==
Строка 36: Строка 36:
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|}
 
|}
 +
  
 
=== Разряд переноса при сложении с неполным слагаемым ===
 
=== Разряд переноса при сложении с неполным слагаемым ===
Строка 68: Строка 69:
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|}
 
|}
 +
  
 
== Троичный полусумматор с одним неполным слагаемым ==
 
== Троичный полусумматор с одним неполным слагаемым ==
Строка 92: Строка 94:
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|-
 
|-
−
|style="background-color:#EEE;padding:2px 30px"| <tex>\bf{z_{sum}}</tex>
+
|style="background-color:#EEE;padding:2px 30px"| <tex>\bf{sum}</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>2</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>2</tex>
Строка 100: Строка 102:
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|-
 
|-
−
|style="background-color:#EEE;padding:2px 30px"| <tex>\bf{z_{transfer}}</tex>
+
|style="background-color:#EEE;padding:2px 30px"| <tex>\bf{transfer}</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 30px"| <tex>0</tex>
Строка 233: Строка 235:
 
|style="background-color:#FFF;padding:2px 10px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>0</tex>
 
|-
 
|-
−
|style="background-color:#EEE;padding:2px 10px"| <tex>\bf{z_{sum}}</tex>
+
|style="background-color:#EEE;padding:2px 10px"| <tex>\bf{sum}</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>2</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>2</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>
Строка 253: Строка 255:
 
|style="background-color:#FFF;padding:2px 10px"| <tex>0</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>0</tex>
 
|-
 
|-
−
|style="background-color:#EEE;padding:2px 10px"| <tex>\bf{z_{transfer}}</tex>
+
|style="background-color:#EEE;padding:2px 10px"| <tex>\bf{transfer}</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>
 
|style="background-color:#FFF;padding:2px 10px"| <tex>1</tex>

Текущая версия на 19:35, 4 сентября 2022

В троичной логике "лжи" и "истине" соответствует [math]-[/math] и [math]+[/math]. Третьему состоянию соответствует [math]0[/math].

Мы будем рассматривать простую троичную функциональную схему — троичный сумматор. В нём используются такие обозначения: [math]\{0, 1, 2\}[/math] (несимметричная троичная система счисления).

Составные части полусумматора

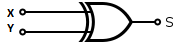
Полусумматор состоит из двух частей: сложения по модулю [math]3[/math] и переноса в следующий разряд.

Логическое сложение по модулю [math]3[/math] при одном неполном слагаемом

Для сложения одного троичного разряда с разрядом переноса.

Результат не меняется при перемене мест операндов.

Сумма по модулю 3
[math]\bf{x_1=x}[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{x_0=y}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{s}[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]2[/math] [math]1[/math] [math]0[/math]


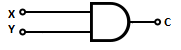
Разряд переноса при сложении с неполным слагаемым

Для сложения одного троичного разряда с разрядом переноса.

Результат не изменяется при перемене мест операндов.

Перенос
[math]\bf{x_1=x}[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{x_0=y}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{c}[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math]


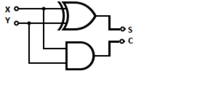
Троичный полусумматор с одним неполным слагаемым

Первая ступень полного троичного сумматора.

Для сложения одного троичного разряда с разрядом переноса.

Результат не изменяется при перемене мест операндов.

[math]\bf{x_1=x}[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{x_0=y}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{sum}[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{transfer}[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math]

transfer содержит разряд переноса, sum содержит сумму по модулю [math]3[/math].

Троичный полусумматор в несимметричной троичной системе счисления

Троичное логическое сложение двух троичных разрядов с разрядом переноса в несимметричной троичной системе счисления.

Результат не изменяется при перемене мест операндов.

Троичный полусумматор можно рассматривать, как объединение двух бинарных троичных функций: «логического сложения по модулю [math]3[/math] в троичной несимметричной системе счисления» и «разряд переноса при сложении двух полных троичных разрядов в троичной несимметричной системе счисления».

Троичный полусумматор
[math]\bf{x_1=x}[/math] [math]2[/math] [math]2[/math] [math]2[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{x_0=y}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{sum}[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{c_{transfer}}[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]2[/math] [math]1[/math] [math]0[/math]

[math]c_{transfer}[/math] — перенос в следующий разряд, несимметричный.

sum — сумма по модулю [math]3[/math], несимметричная.

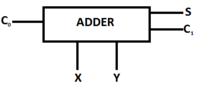
Полное троичное логическое сложение с переносом в несимметричной троичной системе счисления

Полный троичный одноразрядный сумматор является неполной тернарной троичной логической функцией, так как в разряде переноса только два значения [math]0[/math] и [math]1[/math].

Троичный сумматор

Результат не изменяется при перемене мест операндов.

[math]\bf{x_0}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{x_1}[/math] [math]2[/math] [math]2[/math] [math]2[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]2[/math] [math]2[/math] [math]2[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{x_2}[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math]
[math]\bf{sum}[/math] [math]2[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]2[/math] [math]0[/math] [math]2[/math] [math]1[/math] [math]2[/math] [math]1[/math] [math]0[/math]
[math]\bf{transfer}[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math]

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Троичный_сумматор&oldid=85584»