Многомерное дерево Фенвика — различия между версиями
Helm (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 13 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Многомерное [[дерево Фенвика]]''' - структура данных, требующая <tex> O(n^k) </tex> памяти и позволяющая эффективно (за <tex> O(\log^k n) </tex>) | + | '''Многомерное [[дерево Фенвика]]''' (англ. <i> Multidimensional Binary Indexed Tree</i>) {{---}} структура данных, требующая <tex> O(n^k) </tex> памяти и позволяющая эффективно (за <tex> O(\log^k n) </tex>) |
# изменять значение любого элемента в k-мерном массиве; | # изменять значение любого элемента в k-мерном массиве; | ||
# выполнять некоторую ассоциативную, коммутативную, обратимую операцию <tex> G </tex> на k-мерном прямоугольнике <tex> [i_1, \ldots ,i_k] </tex>;<br/> где n - максимальное значение для каждой координаты. | # выполнять некоторую ассоциативную, коммутативную, обратимую операцию <tex> G </tex> на k-мерном прямоугольнике <tex> [i_1, \ldots ,i_k] </tex>;<br/> где n - максимальное значение для каждой координаты. | ||
}} | }} | ||
| + | Рассмотрим для начала дерево Фенвика на примере k-мерного массива с <tex>k = 2</tex>, а затем посмотрим, как можно обобщить его на большие размерности. | ||
Пусть дан массив <tex> A </tex> из <tex> n \times m </tex> элементов: <tex> a_{i,j}</tex>.<br/> | Пусть дан массив <tex> A </tex> из <tex> n \times m </tex> элементов: <tex> a_{i,j}</tex>.<br/> | ||
| − | Деревом Фенвика будем называть массив <tex> T </tex> из <tex> n \times m </tex> элементов: <tex> T_{i,j} = \sum\limits_{k = F(i)}^{i} \sum\limits_{q = F(j)}^{j}a_{k,q}</tex>, где <tex> F(i) = i \& (i + 1) </tex>. | + | Деревом Фенвика будем называть массив <tex> T </tex> из <tex> n \times m </tex> элементов: <tex> T_{i,j} = \sum\limits_{k = F(i)}^{i} \sum\limits_{q = F(j)}^{j}a_{k,q}</tex>, где <tex>F(i) = i\; \&\; (i + 1)</tex>, как и в одномерном [[дерево Фенвика|дереве Фенвика]]. |
==Пример задачи для двумерного случая== | ==Пример задачи для двумерного случая== | ||
| − | |||
Пусть имеем набор точек на плоскости с неотрицательными координатами. Определены 3 операции: | Пусть имеем набор точек на плоскости с неотрицательными координатами. Определены 3 операции: | ||
# добавить точку в <tex>(x, y)</tex>; | # добавить точку в <tex>(x, y)</tex>; | ||
| Строка 16: | Строка 16: | ||
# посчитать количество точек в прямоугольнике <tex>(0, 0), (x, y)</tex>; | # посчитать количество точек в прямоугольнике <tex>(0, 0), (x, y)</tex>; | ||
| − | <tex>n</tex> - количество точек, <tex>maxX</tex> - максимальная <tex>X</tex> координата, <tex>maxY</tex> - максимальная <tex>Y</tex> координата.<br/> | + | <tex>n</tex> {{---}} количество точек, <tex>maxX</tex> {{---}} максимальная <tex>X</tex> координата, <tex>maxY</tex> {{---}} максимальная <tex>Y</tex> координата.<br/> |
Тогда дерево строится за <tex>O(n\cdot\log(maxX)\cdot\log(maxY))</tex>, а запросы выполняются за <tex>O(\log (maxX)\cdot\log (maxY))</tex> | Тогда дерево строится за <tex>O(n\cdot\log(maxX)\cdot\log(maxY))</tex>, а запросы выполняются за <tex>O(\log (maxX)\cdot\log (maxY))</tex> | ||
| − | Добавляя точку вызовем <tex>inc(x, y, 1)</tex>, а удаляя <tex>inc(x, y, -1)</tex>. Таким образом запрос <tex>sum(x, y)</tex> дает количество точек в прямоугольнике. | + | Добавляя точку вызовем <tex>\mathrm{inc}(x, y, 1)</tex>, а удаляя <tex>\mathrm{inc}(x, y, -1)</tex>. Таким образом запрос <tex>\mathrm{sum}(x, y)</tex> дает количество точек в прямоугольнике. |
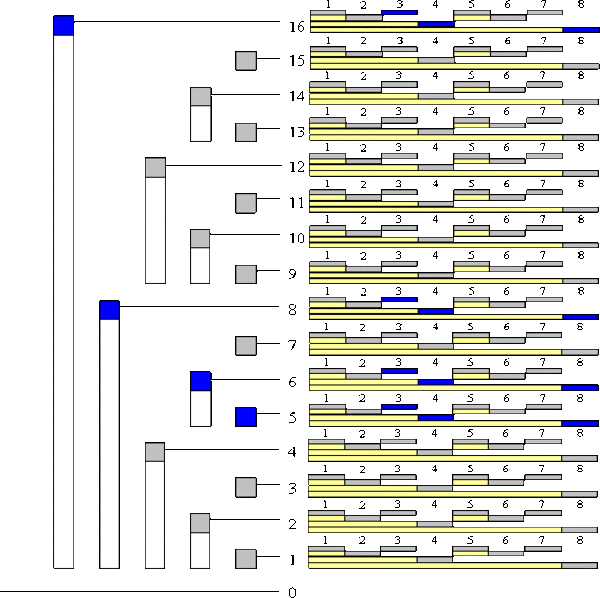
| − | + | [[Файл:example42.gif |thumb|600px|center|Пример дерева Фенвика <tex>(16 \times 8)</tex>. Синим обозначены элементы, которые обновятся при изменении ячейки <tex>(5, 3)</tex>. Чтобы обновить элемент <tex>(X, Y)</tex>, по первой координате нам надо зайти во все столбцы(деревья по второй координате), находящиеся левее <tex>X</tex> и на одной горизонтальной линии с ним, и в каждом из них обновить все ячейки под <tex>Y</tex>(в рамках обозначений данного рисунка).]] | |
| − | < | + | ==Псевдокод== |
| − | + | <tex>\mathtt{t}</tex> {{---}} массив, в котором хранится дерево Фенвика. | |
| − | + | <code style = "display: inline-block;"> | |
| − | + | '''int''' sum(x: '''int''', y: '''int'''): | |
| − | + | '''int''' result = 0 | |
| − | + | '''for''' ('''int''' i = x; i >= 0; i = (i & (i + 1)) - 1) | |
| − | int result = 0 | + | '''for''' ('''int''' j = y; j >= 0; j = (j & (j + 1)) - 1) |
| − | for (int i = x; i >= 0; i = (i & (i+1)) - 1) | + | result += t[i][j]; |
| − | + | '''return''' result; | |
| − | |||
| − | return result; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</code> | </code> | ||
| + | <code style = "display: inline-block;"> | ||
| + | '''func''' inc(x: '''int''', y: '''int''', delta: '''int'''): | ||
| + | '''for''' ('''int''' i = x; i < maxX; i = (i | (i + 1))) | ||
| + | '''for''' ('''int''' j = y; j < maxY; j = (j | (j + 1))) | ||
| + | t[i][j] += delta; | ||
| + | </code> | ||
| + | |||
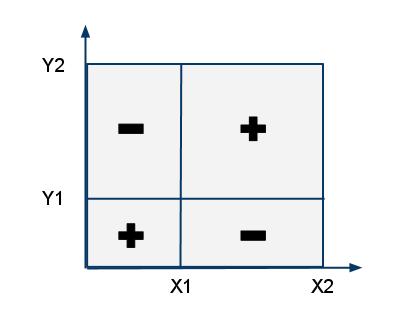
| + | Чтобы посчитать значение функции для прямоугольника <tex>(x_1, y_1), (x_2, y_2)</tex> нужно воспользоваться формулой [[Формула включения-исключения|включения-исключения]]. Например, для суммы: <tex>s = \mathrm{sum}(x_2,y_2)-\mathrm{sum}(x_2,y_1 - 1)-\mathrm{sum}(x_1 - 1,y_2)+\mathrm{sum}(x_1 - 1,y_1 - 1)</tex><br/> | ||
| + | [[Файл:ФормулаВключения-Исключения.jpg]] | ||
| + | |||
| + | ====Обобщение на большие размерности==== | ||
| + | Дерево Фенвика относится к структурам данных, требующим малое количество дополнительной памяти. В комбинации с простым представлением тривиального случая данной структуры это дает возможность легко повышать размерность дерева Фенвика, в котором в ячейках какого-то фиксированного уровня будет находиться дерево меньшей размерности. Для его реализации нам достаточно во всех операциях для каждой новой размерности просто добавить вложенный цикл, пробегающий в ней соответствующие индексы. | ||
| + | |||
| + | ==См. также== | ||
| + | * [[Дерево Фенвика]] | ||
| + | * [[Встречное дерево Фенвика]] | ||
| + | * [[Дерево Фенвика для некоммутативных операций]] | ||
| − | + | ==Источники информации== | |
| + | *[https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/ Topcoder {{---}} Binary Indexed Trees] | ||
| + | *[http://e-maxx.ru/algo/fenwick_tree Дерево Фенвика] | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| − | + | [[Категория: Модификации структур данных]] | |
| − | |||
| − | |||
Текущая версия на 19:07, 4 сентября 2022
| Определение: |
Многомерное дерево Фенвика (англ. Multidimensional Binary Indexed Tree) — структура данных, требующая памяти и позволяющая эффективно (за )
|
Рассмотрим для начала дерево Фенвика на примере k-мерного массива с , а затем посмотрим, как можно обобщить его на большие размерности.
Пусть дан массив из элементов: .
Деревом Фенвика будем называть массив из элементов: , где , как и в одномерном дереве Фенвика.
Содержание
Пример задачи для двумерного случая
Пусть имеем набор точек на плоскости с неотрицательными координатами. Определены 3 операции:
- добавить точку в ;
- удалить точку из ;
- посчитать количество точек в прямоугольнике ;
— количество точек, — максимальная координата, — максимальная координата.
Тогда дерево строится за , а запросы выполняются за
Добавляя точку вызовем , а удаляя . Таким образом запрос дает количество точек в прямоугольнике.
Псевдокод
— массив, в котором хранится дерево Фенвика.
int sum(x: int, y: int):
int result = 0
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
result += t[i][j];
return result;
func inc(x: int, y: int, delta: int):
for (int i = x; i < maxX; i = (i | (i + 1)))
for (int j = y; j < maxY; j = (j | (j + 1)))
t[i][j] += delta;
Чтобы посчитать значение функции для прямоугольника нужно воспользоваться формулой включения-исключения. Например, для суммы:
Обобщение на большие размерности
Дерево Фенвика относится к структурам данных, требующим малое количество дополнительной памяти. В комбинации с простым представлением тривиального случая данной структуры это дает возможность легко повышать размерность дерева Фенвика, в котором в ячейках какого-то фиксированного уровня будет находиться дерево меньшей размерности. Для его реализации нам достаточно во всех операциях для каждой новой размерности просто добавить вложенный цикл, пробегающий в ней соответствующие индексы.