Лемма Бёрнсайда и Теорема Пойа — различия между версиями
Korektur (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 65 промежуточных версий 17 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Иногда требуется провести подсчет комбинаторных объектов с точностью до некоторого отношения эквивалетности. | |
| + | Если это отношение является отношением "с точностью до [[Действие группы на множестве|действия элементом группы]]", то такой подсчет можно провести | ||
| + | с помощью Леммы Бернсайда. | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | Пусть [[Группа|группа]] <tex>G</tex> [[Действие группы на множестве|действует на множество]] <tex>X</tex>. '''Неподвижной точкой''' для элемента <tex>g</tex> называется такой элемент <tex>x</tex>, |
| + | для которого <tex>gx=x</tex>. | ||
}} | }} | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | Множество неподвижных точек элемента <tex>g</tex> называется его '''стабилизатором''' и обозначается <tex>St(g)</tex>. |
}} | }} | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | Пусть группа <tex>G</tex> действует на множество <tex>X</tex>. Будем называть два элемента <tex>x</tex> и <tex>y</tex> эквивалентными, если <tex>x = gy</tex> для некоторого <tex>g \in G</tex>. Классы эквивалентности данного отношения называются '''орбитами''', множество орбит обозначается как <tex>X/G</tex>. |
}} | }} | ||
| − | == Лемма Бёрнсайда == | + | == Лемма Бёрнсайда == |
{{Лемма | {{Лемма | ||
|id=lemmaBerns. | |id=lemmaBerns. | ||
| − | |author= | + | |author=Бернсайд, '''англ.''' Burnside's lemma |
| − | |statement= | + | |statement=Число орбит равно средней мощности стабилизатора элементов группы <tex>G</tex>. <math>|X/G| = \dfrac{1} {|G|}\sum\limits_{g \in G}|St(g)|</math>. |
| + | |proof= | ||
| + | Так как <tex>St(g)</tex> {{---}} стабилизатор элемента <tex>g</tex>, то по определению <math>\sum\limits_{g \in G}|St(g)| = |\{(x, g) \in G\times X \mid g\cdot x = x\}|</math>. | ||
| − | < | + | Следовательно для доказательства леммы необходимо и достаточно доказать следующее равенство: |
| − | + | <math>|X/G|\cdot|G| = |\{(x, g) \in G\times X \mid g\cdot x = x\}|</math> | |
| − | |||
| − | |||
| + | Введем обозначение <tex>C=X/G</tex>. | ||
| − | < | + | Рассмотрим правую часть равенства: |
| + | <math>|\{(x, g) \in G\times X \mid g\cdot x = x\}| = \sum\limits_{x \in X} |G_x| = \sum\limits_{x \in X}</math><math> \dfrac{|G|}{|Gx|} = |G| \sum\limits_{x \in X}\dfrac{1}{|Gx|} </math> | ||
| + | <math>= |G|\sum\limits_{P\in C}\sum\limits_{x\in P}</math><math> \dfrac{1}{|P|}</math> | ||
| + | Заметим, что <math>\sum\limits_{x\in P} \dfrac{1}{|P|} = \dfrac{1}{|P|}\sum\limits_{1}^{|P|}{1} = 1.</math> Следовательно: | ||
| − | + | <math>|G|\sum\limits_{P\in C}\sum\limits_{x\in P} \dfrac{1}{|P|} = |G|\sum\limits_{P\in C} 1</math>. | |
| + | Очевидно, что <math>\sum\limits_{P\in C} 1 = \sum\limits_{1}^{|C|}{1} = |C|.</math> Тогда получим: | ||
| − | + | <math>|G|\sum\limits_{P\in C} 1 = |C|\cdot|G|.</math> | |
| − | + | Откуда следует, что | |
| − | + | <math>\sum\limits_{g \in G}|St(g)| = |C|\cdot|G|.</math> | |
| − | + | ||
}} | }} | ||
| − | == Теорема Пойа == | + | == Теорема Пойа == |
| − | |||
| − | + | Теорема Пойа является обобщением леммы Бёрнсайда. Она также позволяет находить количество классов эквивалентности, но уже используя такую величину, как [[Действие перестановки на набор из элементов, представление в виде циклов|кол-во циклов в перестановке]]. | |
| + | В основе доказательства теоремы Пойа лежит лемма Бёрнсайда. | ||
{{Теорема | {{Теорема | ||
|id=teorPo. | |id=teorPo. | ||
| − | |author=Пойа | + | |author=Пойа, '''англ.''' Pólya enumeration theorem |
| − | |statement= < | + | |statement= <math>C = \dfrac{1}{|G|}\sum\limits_{g \in G} l^{P(g)}</math> ,где <tex>C</tex> {{---}} кол-во различных классов эквивалентности, <tex>P(g)</tex> {{---}} кол-во циклов в перестановке <tex>g</tex>, <tex>l</tex> {{---}} кол-во различных состояний одного элемента. |
| − | |proof=Для доказательства этой | + | |proof=Для доказательства этой теоремы достаточно установить следующее равенство |
| − | < | + | <math>|St(g)| = l^{P(g)}</math> |
| + | |||
| + | Рассмотрим некоторую перестановку <tex>g</tex> и некоторый элемент <tex>f</tex>. Под действием перестановки <tex>g</tex> элементы <tex>f</tex> передвигаются, как известно, по циклам перестановки. Заметим, что так как в результате должно получаться <tex>fg = f</tex>, то внутри каждого цикла перестановки должны находиться одинаковые элементы <tex>f</tex>. В то же время, для разных циклов никакой связи между значениями элементов не возникает. Таким образом, для каждого цикла перестановки <tex>g</tex> мы выбираем по одному значению, и, тем самым, мы получим все представления <tex>f</tex>, инвариантные относительно этой перестановки, т.е.: | ||
| + | <math>|St(g)| = l^{P(g)}</math> | ||
| + | }} | ||
| − | + | ==Задача о числе раскрасок прямоугольника== | |
| − | + | {{Задача | |
| + | |definition=Выведите формулу для числа раскрасок прямоугольника <tex>[n \times m]</tex> в <tex>k</tex> цветов с точностью до отражения относительно горизонтальной и вертикальной оси. | ||
}} | }} | ||
| + | Решим данную задачу, воспользуясь леммой Бёрнсайда. | ||
| + | |||
| + | '''Решение''' | ||
| + | |||
| + | Для начала определим, какие операции определены на группе <tex>G</tex> {{---}} это операция "отражение относительно горизонтальной оси", обозначим ее как <tex>\alpha</tex>, "отражение относительно вертикальной оси" {{---}} <tex>\beta</tex> и "переход из одного состояния в него же" {{---}} <tex>e</tex>. | ||
| + | Таким образом, <tex>G</tex> содержит 4 комбинации операций: <tex>G = \{e, \alpha, \beta, \alpha \circ \beta \}</tex>. | ||
| + | Стоит уделить особое внимание тому факту, что никакие иные комбинации функций <tex>\alpha</tex> и <tex>\beta</tex> не были включены в <tex>G</tex>. Это объясняется довольно просто: очевидно то, что операции коммутативны, то есть <tex>\alpha \circ \beta = \beta \circ \alpha</tex>, а также то, что <tex>\alpha \circ \alpha = \beta \circ \beta = e</tex>, тогда любая комбинация данных функций может быть упрощена до вышеперечисленных (в <tex>G</tex>) путем совмещения одинаковых и замены их на <tex>e</tex>. | ||
| + | |||
| + | Отметим также то, что количество раскрасок прямоугольника <tex>[m \times n]</tex> в <tex>k</tex> цветов: | ||
| + | :1. С точностью до операции <tex>\alpha</tex> при нечетном <tex>m</tex> равно количеству раскрасок прямоугольника <tex>[m-1 \times n]</tex> в <tex>k</tex> цветов. | ||
| + | :2. С точностью до операции <tex>\beta</tex> при нечетном <tex>n</tex> равно количеству раскрасок прямоугольника <tex>[m \times n-1]</tex> в <tex>k</tex> цветов. | ||
| + | :3. С точностью до операции <tex>\alpha \circ \beta</tex> при нечетных <tex>n</tex> и <tex>m</tex> равно количеству раскрасок прямоугольника <tex>[m-1 \times n-1]</tex> в <tex>k</tex> цветов (а также частные случаи, когда <tex>n</tex> или <tex>m</tex> нечетные). | ||
| + | Данное множество фактов объясняется тем, что мы можем как бы "слить" вместе два столбика (и\или) столбца, при этом с точностью до нужного действия количество раскрасок не уменьшится. | ||
| + | |||
| + | Количество неподвижных точек в случае с действием <tex>e</tex> равно <tex>k^{nm}</tex>, так как ни одна раскрашенная клетка не повторилась при действии нулевого действия. Для действий <tex>\alpha</tex> и <tex>\beta</tex> количество раскрасок будет <tex>k^{\lceil \dfrac{m}{2} \rceil n}</tex> и <tex>k^{{\lceil {\dfrac{n}{2}} \rceil}m}</tex> соответственно, для их композиции количество раскрасок <tex>k^{{\lceil {\dfrac{nm}{2}} \rceil}}</tex>, так как верхняя левая четверть прямоугольника однозначно задаёт правую нижнюю, аналогично с правой верхней. | ||
| + | |||
| + | Тогда воспользуемся Леммой Бёрнсайда и определим количество таких раскрасок. | ||
| + | |||
| + | :<tex> |C| = \dfrac{1} {|G|} \sum\limits_{g \in G}|St(g)| = \dfrac{I_1 + I_2 + I_3 + I_4}{4} = \dfrac{k^{nm}+k^{\lceil \dfrac{m}{2} \rceil n} + k^{{\lceil {\dfrac{n}{2}} \rceil}m} + k^{{\lceil {\dfrac{nm}{2}} \rceil}}}{4}</tex> | ||
| + | |||
| + | ==Задача о числе раскрасок граней куба== | ||
| + | {{Задача | ||
| + | |definition=Выведите формулу для числа раскрасок граней куба в <tex>k</tex> цветов с точностью до поворота. | ||
| + | }} | ||
| + | Как и в предыдущей задаче, будем использовать в решении лемму Бёрнсайда. | ||
| + | |||
| + | '''Решение''' | ||
| + | |||
| + | Рассмотрим группу вращений куба <tex>G</tex>: | ||
| + | |||
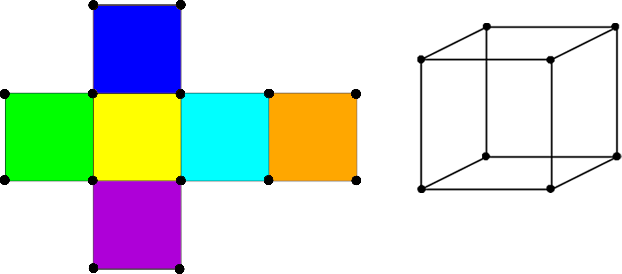
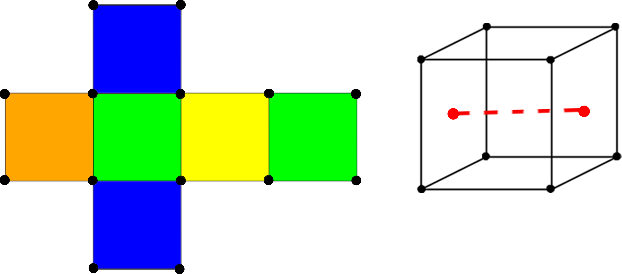
| + | ''Последующие изображения с развертками будут подразумевать такое же соответствие вершин, как на рисунке ниже. На развертках будем показывать раскраски, а на самом кубе ребро, через которое мы будем вращать его. Цвета на развертке лишь показывают то, что грани с одинаковым цветом должны быть одинаково раскрашены.'' | ||
| + | [[Файл:burnside-intro.png|top]] | ||
| + | * <tex>1</tex> Тождественное вращение. Поскольку ничего не происходит, мы можем покрасить каждую грань в любой цвет <tex>\Rightarrow k^6 </tex> раскрасок. | ||
| + | [[Файл:burnside-1.png|top]] | ||
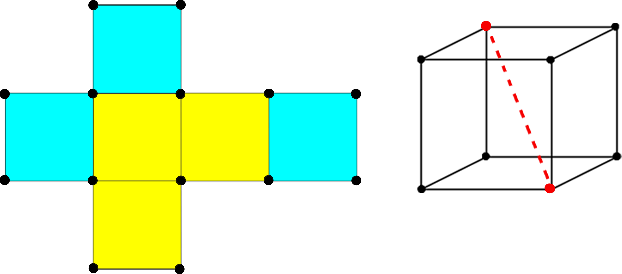
| + | * <tex>4</tex> вращения на угол <tex>120^{\circ}</tex> и <tex>4</tex> вращения на угол <tex>240^{\circ}</tex> вдоль главных диагоналей куба (вращений четыре, поскольку главных диагоналей <tex>4</tex> шт.). При вращении, если одна грань переходит в другую, мы должны покрасить их в один цвет. Такие раскраски будут являться стабилизатором данного вращения. Из рисунка видно, что мы можем покрасить наш куб в <tex>k^2</tex> цветов (в <tex>k</tex> цветов одни три грани и в <tex>k</tex> цветов другие три грани). | ||
| + | [[Файл:burnside-2.png|top]] | ||
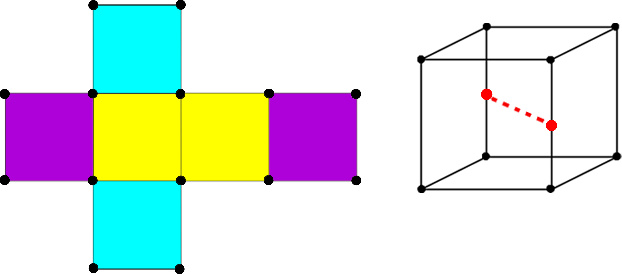
| + | * <tex>6</tex> вращений на угол <tex>180^{\circ}</tex> вдоль осей, соединяющих середины противоположных ребер <tex>\Rightarrow k^3 </tex> раскрасок. | ||
| + | [[Файл:burnside-3.png|top]] | ||
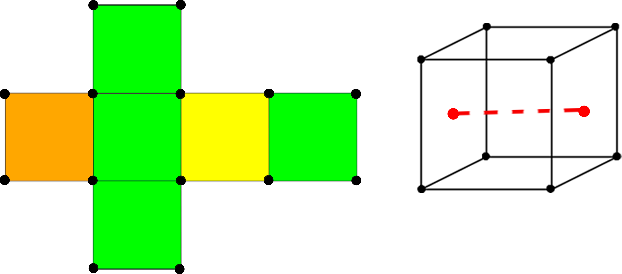
| + | * <tex>3</tex> вращения на угол <tex>90^{\circ}</tex> и <tex>3</tex> вращения на угол <tex>270^{\circ}</tex> вдоль осей, соединяющих центры противоположных граней <tex>\Rightarrow k^3 </tex> раскрасок. | ||
| + | [[Файл:burnside-4.png|top]] | ||
| + | * <tex>3</tex> вращения на угол <tex>180^{\circ}</tex> вдоль осей, соединяющих центры противоположных граней <tex>\Rightarrow k^4 </tex> раскрасок. | ||
| + | [[Файл:burnside-5.png|top]] | ||
| + | |||
| + | Итого <tex>1+(4+4)+6+(3+3)+3=24</tex> поворота, при которых куб переходит в себя. Других различных поворотов, которые переводят куб в себя, не существует, поскольку ''группа вращений'' [https://en.wikipedia.org/wiki/Octahedral_symmetry <tex>G</tex> изоморфна ''симметрической группе'' <tex>S_4</tex>], тогда из того, что <tex>|S_4|=24</tex> следует, что мы указали все преобразования, которые переводят куб в себя, причем различным образом. | ||
| + | |||
| + | Теперь с помощью Леммы Бёрнсайда найдем искомый ответ: | ||
| + | |||
| + | :<tex> |C| = \dfrac{1} {|G|} \sum\limits_{g \in G}|St(g)| = \dfrac{1} {24} (k^6 + 8k^2 + 6k^3 + 6k^3 + 3k^4) = \dfrac{1} {24} (k^6 + 3k^4 + 12k^3 + 8k^2)</tex> | ||
==См. также== | ==См. также== | ||
| − | * [http:// | + | * [[Теорема Кэли|Теорема Кэли]] |
| − | * [http:// | + | * [[Задача об ожерельях|Задача об ожерельях]] |
| + | |||
| + | ==Источники информации== | ||
| + | *[http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%BC%D0%BC%D0%B0_%D0%91%D1%91%D1%80%D0%BD%D1%81%D0%B0%D0%B9%D0%B4%D0%B0 Википедия {{---}} Лемма Бёрнсайда] | ||
| + | *[http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9F%D0%BE%D0%B9%D0%B0 Википедия {{---}} Теорема Пойа] | ||
| + | *[https://en.wikipedia.org/wiki/Burnside%27s_lemma Wikipedia {{---}} Burnside's lemma] | ||
| + | *[https://en.wikipedia.org/wiki/P%C3%B3lya_enumeration_theorem Wikipedia {{---}} Pólya enumeration theorem] | ||
| − | |||
| − | |||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Комбинаторика]] | [[Категория: Комбинаторика]] | ||
| + | [[Категория: Теория групп]] | ||
Текущая версия на 19:31, 4 сентября 2022
Иногда требуется провести подсчет комбинаторных объектов с точностью до некоторого отношения эквивалетности. Если это отношение является отношением "с точностью до действия элементом группы", то такой подсчет можно провести с помощью Леммы Бернсайда.
| Определение: |
| Пусть группа действует на множество . Неподвижной точкой для элемента называется такой элемент , для которого . |
| Определение: |
| Множество неподвижных точек элемента называется его стабилизатором и обозначается . |
| Определение: |
| Пусть группа действует на множество . Будем называть два элемента и эквивалентными, если для некоторого . Классы эквивалентности данного отношения называются орбитами, множество орбит обозначается как . |
Лемма Бёрнсайда
| Лемма (Бернсайд, англ. Burnside's lemma): |
Число орбит равно средней мощности стабилизатора элементов группы . . |
| Доказательство: |
|
Так как — стабилизатор элемента , то по определению . Следовательно для доказательства леммы необходимо и достаточно доказать следующее равенство: Введем обозначение . Рассмотрим правую часть равенства: Заметим, что Следовательно: . Очевидно, что Тогда получим:
Откуда следует, что |
Теорема Пойа
Теорема Пойа является обобщением леммы Бёрнсайда. Она также позволяет находить количество классов эквивалентности, но уже используя такую величину, как кол-во циклов в перестановке. В основе доказательства теоремы Пойа лежит лемма Бёрнсайда.
| Теорема (Пойа, англ. Pólya enumeration theorem): |
,где — кол-во различных классов эквивалентности, — кол-во циклов в перестановке , — кол-во различных состояний одного элемента. |
| Доказательство: |
|
Для доказательства этой теоремы достаточно установить следующее равенство
|
Задача о числе раскрасок прямоугольника
| Задача: |
| Выведите формулу для числа раскрасок прямоугольника в цветов с точностью до отражения относительно горизонтальной и вертикальной оси. |
Решим данную задачу, воспользуясь леммой Бёрнсайда.
Решение
Для начала определим, какие операции определены на группе — это операция "отражение относительно горизонтальной оси", обозначим ее как , "отражение относительно вертикальной оси" — и "переход из одного состояния в него же" — . Таким образом, содержит 4 комбинации операций: .
Стоит уделить особое внимание тому факту, что никакие иные комбинации функций и не были включены в . Это объясняется довольно просто: очевидно то, что операции коммутативны, то есть , а также то, что , тогда любая комбинация данных функций может быть упрощена до вышеперечисленных (в ) путем совмещения одинаковых и замены их на .
Отметим также то, что количество раскрасок прямоугольника в цветов:
- 1. С точностью до операции при нечетном равно количеству раскрасок прямоугольника в цветов.
- 2. С точностью до операции при нечетном равно количеству раскрасок прямоугольника в цветов.
- 3. С точностью до операции при нечетных и равно количеству раскрасок прямоугольника в цветов (а также частные случаи, когда или нечетные).
Данное множество фактов объясняется тем, что мы можем как бы "слить" вместе два столбика (и\или) столбца, при этом с точностью до нужного действия количество раскрасок не уменьшится.
Количество неподвижных точек в случае с действием равно , так как ни одна раскрашенная клетка не повторилась при действии нулевого действия. Для действий и количество раскрасок будет и соответственно, для их композиции количество раскрасок , так как верхняя левая четверть прямоугольника однозначно задаёт правую нижнюю, аналогично с правой верхней.
Тогда воспользуемся Леммой Бёрнсайда и определим количество таких раскрасок.
Задача о числе раскрасок граней куба
| Задача: |
| Выведите формулу для числа раскрасок граней куба в цветов с точностью до поворота. |
Как и в предыдущей задаче, будем использовать в решении лемму Бёрнсайда.
Решение
Рассмотрим группу вращений куба :
Последующие изображения с развертками будут подразумевать такое же соответствие вершин, как на рисунке ниже. На развертках будем показывать раскраски, а на самом кубе ребро, через которое мы будем вращать его. Цвета на развертке лишь показывают то, что грани с одинаковым цветом должны быть одинаково раскрашены.
- Тождественное вращение. Поскольку ничего не происходит, мы можем покрасить каждую грань в любой цвет раскрасок.
- вращения на угол и вращения на угол вдоль главных диагоналей куба (вращений четыре, поскольку главных диагоналей шт.). При вращении, если одна грань переходит в другую, мы должны покрасить их в один цвет. Такие раскраски будут являться стабилизатором данного вращения. Из рисунка видно, что мы можем покрасить наш куб в цветов (в цветов одни три грани и в цветов другие три грани).
- вращений на угол вдоль осей, соединяющих середины противоположных ребер раскрасок.
- вращения на угол и вращения на угол вдоль осей, соединяющих центры противоположных граней раскрасок.
- вращения на угол вдоль осей, соединяющих центры противоположных граней раскрасок.
Итого поворота, при которых куб переходит в себя. Других различных поворотов, которые переводят куб в себя, не существует, поскольку группа вращений изоморфна симметрической группе , тогда из того, что следует, что мы указали все преобразования, которые переводят куб в себя, причем различным образом.
Теперь с помощью Леммы Бёрнсайда найдем искомый ответ: