Действие перестановки на набор из элементов, представление в виде циклов
Содержание
Действие перестановки на набор элементов
| Определение: |
| Пусть — перестановка из элементов, и — множество некоторых объектов, занумерованных числами от до . Тогда результатом действия перестановки на этот набор объектов назовём множество объектов , занумерованных числами от одного до , причём . |
Обозначим за множество (не пронумерованных) объектов . Поскольку перестановку можно рассматривать как отображение , а нумерацию как отображение , то действие перестановки можно определить как композицию отображений .
Например, рассмотрим множество и перестановку . Тогда результат действия на — упорядоченное множество . Если рассмотреть граф перестановки (описано ниже), то действие перестановки можно представить таким образом: каждый элемент устанавливается в вершину графа, соответствующую номеру этого элемента, после чего каждый элемент передвигается по исходящему из этой вершины ребру.
Также, композицию перестановок можно выразить как действие одной перестановки на другую. Стоит отметить, что действие перестановки соответствует переходу по графу раз.
Действие обратной перестановки над множеством соответствует переходу элементов по развёрнутым рёбрам и даёт упорядоченное множество , для которого верно .
| Утверждение: |
Если , то ; |
| Поскольку можно представить как , то |
Циклы
| Определение: |
| Циклом длины называется такая перестановка которая тождественна на всём множестве кроме подмножества и , . Обозначается . |
Перестановку можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: .
Цикл может быть записан по разному, например, в приведенном выше примере цикл может быть записан как , , но не может быть записан как .
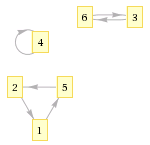
Перестановку можно представить в виде графа. Граф содержит ребро от вершины к вершине если . Тогда циклы перестановки соответствуют циклическим путям в графе.
С циклами связаны некоторые интересные свойства перестановок.
| Определение: |
| Степенью перестановки называется минимальное число такое, что |
| Утверждение: |
Степень перестановки равна наименьшему общему кратному длин всех циклов |
| Пусть — степень перестановки. Граф перестановки разбит на циклы, и для того, чтобы какой-то элемент прошёл по своему циклу один раз, нужно возвести перестановку в степень , где — длина цикла. Если элемент проходит цикл несколько раз и возвращается на своё место, то можно сделать вывод о том, что перестановка возводится в степень кратную . Тогда только в том случае, когда делится на длины всех циклов, все элементы вернутся на свои места, а наименьшее такое — это НОК длин всех циклов. |
| Утверждение: |
Если длины всех циклов не превышают , то перестановка является инволюцией. |
| Действительно, в таком случае по вышеупомянутому . Домножив на получим . |
Поиск всех циклов в перестановке
| Задача: |
| Дана перестановка из элементов, требуется найти все циклы в ней. |
Рассмотрим элемент перестановки . Добавим его к циклу, отметим позицию посещенной и перейдем к . Если мы перешли в позицию , которую уже посещали, значит мы нашли очередной цикл перестановки. Перейдем к первой непосещенной позиции и продолжим поиск.
Рассмотрим в качестве примера поиск циклов в перестановке :
- В позиции находится число . Добавим его к новому циклу и перейдем в позицию . Аналогично добавим к циклу числа и . Перейдем в позицию , которую мы уже посещали — нашли первый цикл .
- Аналогично найдем второй цикл .
- Таким образом,
Псевдокод алгоритма
function findCycles(int p[]):
vector<bool> used(n) // массив, где отмечены посещенные позиции
for i = 1 to n
if not used[i]
j = i
vector<int> cycle
while not used[j]
cycle.push_back(p[j])
used[j] = true
j = p[j]
print cycle // выведем на экран очередной цикл перестановки