Квадродеревья — различия между версиями
Gromak (обсуждение | вклад) м (переименовал Квадродеревья и перечисление точек в произвольном прямоугольнике (статика) в Квадродеревья: Что-то пошло не так) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 4 промежуточные версии 3 участников) | |||
| Строка 16: | Строка 16: | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Глубина квадродерева для множества точек <tex>P</tex> не превосходит <tex>\log_2(s / c) + | + | Глубина квадродерева для множества точек <tex>P</tex> не превосходит <tex>\log_2(s / c) + 1/2</tex>, где <tex>c</tex> {{---}} наименьшее расстояние между двумя точками из <tex>P</tex>, а <tex>s</tex> {{---}} сторона квадрата, с которого начинается построение квадродерева. |
|proof= | |proof= | ||
Сторона квадрата на глубине <tex>i</tex>, очевидно, равна <tex>s / 2^i</tex>. Максимальное расстояние между двумя точками внутри квадрата достигается, когда они являются вершинами диагонали, то есть на глубине <tex>i</tex> расстояние между любыми двумя точками в одном квадрате не превосходит <tex>s \sqrt 2 / 2^i</tex>. Поскольку внутренняя вершина квадродерева содержит хотя бы 2 точки в соответствующем ей квадрате, то <tex>s \sqrt 2 / 2^i \geq c</tex>, так как <tex>c</tex> {{---}} минимальное расстояние между точками в <tex>P</tex>. Отсюда следует, что <tex>i \leq \log_2(s \sqrt 2 / c) = \log_2 (s / c) + 1/2</tex>. Значит, глубина любой внутренней вершины не превосходит <tex>\log_2 (s / c) + 1/2</tex>, из чего следует утверждение леммы (так как самый глубокий лист лежит на 1 глубже самой глубокой внутренней вершины). | Сторона квадрата на глубине <tex>i</tex>, очевидно, равна <tex>s / 2^i</tex>. Максимальное расстояние между двумя точками внутри квадрата достигается, когда они являются вершинами диагонали, то есть на глубине <tex>i</tex> расстояние между любыми двумя точками в одном квадрате не превосходит <tex>s \sqrt 2 / 2^i</tex>. Поскольку внутренняя вершина квадродерева содержит хотя бы 2 точки в соответствующем ей квадрате, то <tex>s \sqrt 2 / 2^i \geq c</tex>, так как <tex>c</tex> {{---}} минимальное расстояние между точками в <tex>P</tex>. Отсюда следует, что <tex>i \leq \log_2(s \sqrt 2 / c) = \log_2 (s / c) + 1/2</tex>. Значит, глубина любой внутренней вершины не превосходит <tex>\log_2 (s / c) + 1/2</tex>, из чего следует утверждение леммы (так как самый глубокий лист лежит на 1 глубже самой глубокой внутренней вершины). | ||
| Строка 86: | Строка 86: | ||
Сжатое квадродерево для <tex>n</tex> точек имеет <tex>O(n)</tex> вершин и глубину <tex>O(n)</tex>. | Сжатое квадродерево для <tex>n</tex> точек имеет <tex>O(n)</tex> вершин и глубину <tex>O(n)</tex>. | ||
|proof= | |proof= | ||
| − | Как отмечалось в представленной выше теореме, достаточно доказать оценку <tex>O(n)</tex> | + | Как отмечалось в представленной выше теореме, достаточно доказать оценку <tex>O(n)</tex> для числа интересных квадратов. Докажем по индукции, что в квадродереве для <tex>n</tex> точек количество интересных квадратов меньше либо равно <tex>n</tex>: |
* для <tex>n = 1</tex> это очевидно; | * для <tex>n = 1</tex> это очевидно; | ||
| − | * пусть | + | * пусть доказано для квадродерева для <tex>n - 1</tex> точек. Добавим новую точку <tex>x</tex>: сначала найдём наименьший интересный квадрат <tex>p(x)</tex>, который её содержит. Если <tex>x</tex> находится в его пустой четверти, то просто добавляем <tex>x</tex> как лист, не изменив число интересных квадратов. Если же четверть <tex>p(x)</tex> в которую необходимо вставить <tex>x</tex>, уже содержит точку <tex>y</tex>( или интересный квадрат <tex>r</tex>), то мы можем добавить в дерево интересный квадрат, который будет содержать <tex>x</tex> и <tex>y</tex> в разных четвертях. Таким образом, при добавлении точки мы увеличиваем количество интересных квадратов не более, чем на один. |
| − | |||
| − | |||
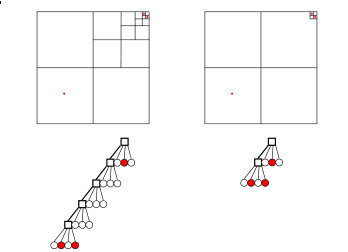
Таким образом, квадродерево для <tex>n</tex> точек имеет <tex>O(n)</tex> вершин. Глубина, очевидно, тоже <tex>O(n)</tex>, поскольку на каждом уровне есть хотя бы одна вершина (здесь под вершинами имеются в виду узлы в дереве). При этом оценки получше нет (то есть глубина <tex>\Theta(n)</tex>). На картинке в правом дереве можно на место левого нижнего красного кружка поставить опять такое дерево и так делать сколь угодно долго, получим глубину <tex>\Theta(n)</tex>. | Таким образом, квадродерево для <tex>n</tex> точек имеет <tex>O(n)</tex> вершин. Глубина, очевидно, тоже <tex>O(n)</tex>, поскольку на каждом уровне есть хотя бы одна вершина (здесь под вершинами имеются в виду узлы в дереве). При этом оценки получше нет (то есть глубина <tex>\Theta(n)</tex>). На картинке в правом дереве можно на место левого нижнего красного кружка поставить опять такое дерево и так делать сколь угодно долго, получим глубину <tex>\Theta(n)</tex>. | ||
Текущая версия на 19:05, 4 сентября 2022
В списке билетов была опечатка, поэтому возникла путаница во многих местах. В этой статье оставляю просто всё полезное (и не очень) про квадродеревья, потому что нужно для скип-квадродерева.
Содержание
Определение и построение
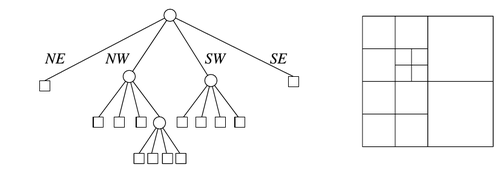
Квадродерево — дерево, каждая внутренняя вершина которого содержит 4 ребёнка. Любому узлу квадродерева соответствует некоторый квадрат. Если внутренней вершине соответствует какой-то квадрат , то её детям соответствуют четверти квадрата (см. картинку).
Вообще говоря, квадродеревья могут быть использованы для разных целей и хранить разные данные, но мы хранить в них будем какой-то набор точек на плоскости.
Пусть дано множество точек , для которого нужно построить квадродерево. Начнём с некоторого квадрата , содержащего все точки из . Если он не дан явно, его можно легко найти за линейное время от числа вершин. Пусть . Обозначим . Тогда:
- если содержит не больше одной точки, то квадродерево состоит из одного листа, которому соответствует квадрат ;
- иначе корнем дерева делаем вершину , которой соответствует квадрат , а её дети — , и им соответствуют квадраты , , , . Затем таким же образом рекурсивно превращаем каждого ребёнка в квадродерево для множества точек, лежащих в соответствующих четвертях.
Леммы и теоремы
Сперва оценим глубину квадродерева. Если какие-то две точки лежат очень близко, то процесс построения может продолжаться очень долго, поэтому глубину невозможно оценить функцией от числа вершин.
| Лемма: |
Глубина квадродерева для множества точек не превосходит , где — наименьшее расстояние между двумя точками из , а — сторона квадрата, с которого начинается построение квадродерева. |
| Доказательство: |
| Сторона квадрата на глубине , очевидно, равна . Максимальное расстояние между двумя точками внутри квадрата достигается, когда они являются вершинами диагонали, то есть на глубине расстояние между любыми двумя точками в одном квадрате не превосходит . Поскольку внутренняя вершина квадродерева содержит хотя бы 2 точки в соответствующем ей квадрате, то , так как — минимальное расстояние между точками в . Отсюда следует, что . Значит, глубина любой внутренней вершины не превосходит , из чего следует утверждение леммы (так как самый глубокий лист лежит на 1 глубже самой глубокой внутренней вершины). |
Также можно заметить, что в идеальном случае дерево будет полностью сбалансировано (то есть размеры всех детей каждой внутренней вершины одинаковы), и тогда глубина составит порядка логарифма от числа вершин.
Размер дерева и время построения будут также зависеть и от — мощности .
| Теорема: |
Квадродерево глубины для точек содержит вершин и может быть построено за . |
| Доказательство: |
|
Поскольку каждая внутренняя вершина имеет четырёх детей, то суммарное число листьев будет , где — число внутренних вершин. Поэтому достаточно доказать оценки лишь для внутренних вершин. Каждая внутренняя вершина содержит хотя бы одну точку в соответствующем ей квадрате. Заметим, что квадраты с одного уровня не пересекаются и полностью покрывают весь исходный квадрат (в котором точек). Значит, число внутренних вершин одного уровня не может превосходить . Из этого следует, что всего внутренних вершин . При построении квадродерева наиболее длительная операция на каждом шаге — распределение точек по четвертям текущего квадрата. Таким образом, время, затрачиваемое на одну внутреннюю вершину, линейно зависит от числа точек в соответствующем ей квадрате. Как отмечалось выше, на одном уровне суммарно во всех внутренних вершинах не больше точек, из чего следует доказываемая оценка. |
Перечисление точек в произвольном прямоугольнике
В этом разделе написаны сомнительные вещи и вообще он не нужен, можно не читать. Пусть на вход подаётся некоторый прямоугольник , для которого надо вернуть все точки из множества , которые принадлежат этому прямоугольнику.
Алгоритм следующий:
- если мы лист, то просто проверяем, лежит ли наша точка в , и возвращаем её, если да;
- иначе запускаемся от детей и возвращаем объединение всего того, что вернули дети.
Псевдокод можно посмотреть здесь. Там немного по-другому (хранят не больше 4-х точек в каждой вершине дерева, а у нас подразумевается, что точки явно хранятся только в листьях), но в целом почти такой же.
Если совсем кратко, то запрос выглядит так:
QTree-RangeSearch(P, M):
if (P is a leaf) then
if (P.point in M) then
report P.point
for each child C of P do
if C.region intersects M then
QTree-RangeSearch(C, M)
Тут говорят, что работает за . Ну а вообще, можно делать по-тупому (без квадродерева, просто храня точки в списке или векторе) за , тупо проверяя все точки, но, видимо, так на практике быстрее получается. Не очень понятно, используются ли вообще обычные квадродеревья кем-либо для этой цели.
Насчёт времени работы: понятно, что если какая-то вершина, попадающая в ответ, находится на дне дерева, то будет работать минимум за глубину. При этом в ответе могут быть примерно все точки, поэтому будет работать минимум за . Отсюда . Поскольку вершин в дереве , то очевидно, что будет работать не дольше, чем . Но, судя по всему, тоже верная оценка.
Собственно, осталось доказать, что на запрос, и конспект готов.
Короче, я не знаю, как это доказать, и мне кажется, что это не так. Если нам подали прямоугольник, содержащий все точки, то мы пройдём по всем вершинам, которых (так написано в книжке, и лучшей оценки, видимо, нет). Возможно, я неправильно понимаю, что от нас хотят. Может быть, можно придумать какие-то оптимизации, ибо так совсем печальная оценка на запрос получается. Также могу предположить, что оценку времени можно улучшить, использовав функцию от размера ответа, но опять же не могу придумать/найти, как это сделать.
Сбалансированное квадродерево
Квадродерево называется сбалансированным, если для соответствующего ему разбиения плоскости на квадраты верно, что для любых двух соседних квадратов их стороны отличаются не более чем в два раза.
Они нужны для каких-то там задач, но нам не нужны, поэтому ничего писать не буду.
Сжатое квадродерево
Обычное квадродерево может иметь слишком большую глубину независимо от количества точек. Сжатое дерево лишено данного недостатка, имея глубину , и на его основе строится Skip Quadtree.
| Определение: |
| Назовём квадрат интересным, если соответствующая ему вершина дерева имеет хотя бы 2 непустых ребёнка (то есть таких, что в их квадратах содержится хотя бы одна точка) или является корнем. |
Понятно, что любой квадрат , содержащий хотя бы две точки, содержит единственный наибольший интересный квадрат. Сжатое квадродерево получается сжатием обычного таким образом, чтобы остались только интересные квадраты. Пустые дети неинтересных квадратов удаляются. Для каждого интересного квадрата будем хранить 4 указателя для каждой четверти этого квадрата. Если четверть содержит две или более точки, то указатель ссылается на наибольший интересный квадрат в этой четверти. Если четверть содержит одну точку, то указатель ссылается на эту точку. Наконец, если четверть не содержит точек, то указатель сделаем нулевым. Картинка проясняет ситуацию. Квадратикам соответствуют интересные квадраты, красным кружкам — точки, белым кружкам — пустота.
О размерах сжатого квадродерева
| Лемма: |
Сжатое квадродерево для точек имеет вершин и глубину . |
| Доказательство: |
|
Как отмечалось в представленной выше теореме, достаточно доказать оценку для числа интересных квадратов. Докажем по индукции, что в квадродереве для точек количество интересных квадратов меньше либо равно :
|
Операции над сжатым квадродеревом
Все операции похожи на аналогичные в обычных деревьях поиска. Только они делаются за . Того же самого можно добиться, храня точки просто в списке или векторе. Хотя на практике, наверно, так побыстрее. Но всё же сама по себе структура не особо полезна, зато пополезнее будет Skip Quadtree.
Поиск
Нам дают точку, хотим найти наименьший интересный квадрат, который её содержит (содержит геометрически, в самом дереве её может не быть, тут, возможно, правильнее сказать «пересекает»). Довольно очевидно, как это делать: просто идём вниз по дереву в нужную четверть, начиная с корня. В какой-то момент закончим, найдя наименьший интересный квадрат, который содержит искомую точку. Дальше легко проверить, есть ли такая точка в квадродереве. Работает, очевидно, за высоту, которая линейно зависит от числа точек (см. выше).
Вставка
Сначала запускаем поиск, находим наименьший квадрат, в который надо вставиться, понимаем, в какую четверть вставляться. Если она пустая, то всё совсем просто, меняем 1 указатель. Если там есть точка, то добавим новый интересный квадрат, поправим указателей, и всё хорошо. Таким образом, нужно сделать поиск за и ещё действий.
Удаление
Начнём, разумеется, с поиска. Если такая точка есть, то обнулим поинтер на неё, при этом квадрат, который был интересный, может больше не быть интересным. При этом родитель этого квадрата всё равно останется интересным. Значит, в таком случае просто заменим этот квадрат на точку. В общем, тут тоже из-за поиска и на само удаление.
Литература
- van Kreveld, de Berg, Overmars, Cheong — Computational Geometry. Algorithms and Applications. Страница 309. Тут можно почитать про квадродеревья.
- Статья на архиве про Skip Quadtree Тут можно почитать про сжатое квадродерево.
- Квадродерево на Википедии
- Даже на русский переведено, оказывается