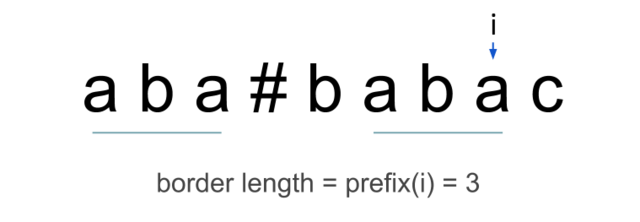Алгоритм Кнута-Морриса-Пратта — различия между версиями
Shersh (обсуждение | вклад) (→Оценка по памяти) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 13 промежуточных версий 5 участников) | |||
| Строка 4: | Строка 4: | ||
Дана цепочка <tex>T</tex> и образец <tex>P</tex>. Требуется найти все позиции, начиная с которых <tex>P</tex> входит в <tex>T</tex>. | Дана цепочка <tex>T</tex> и образец <tex>P</tex>. Требуется найти все позиции, начиная с которых <tex>P</tex> входит в <tex>T</tex>. | ||
<br> | <br> | ||
| − | Построим строку <tex>S = P\#T</tex>, где <tex>\#</tex> — любой символ, не входящий в алфавит <tex>P</tex> и <tex>T</tex>. Посчитаем на ней значение [[Префикс-функция|префикс-функции]]. Благодаря разделительному символу <tex>\#</tex>, выполняется <tex>\forall i: | + | Построим строку <tex>S = P\#T</tex>, где <tex>\#</tex> — любой символ, не входящий в алфавит <tex>P</tex> и <tex>T</tex>. Посчитаем на ней значение [[Префикс-функция|префикс-функции]] <tex> p </tex>. Благодаря разделительному символу <tex>\#</tex>, выполняется <tex>\forall i: p[i] \leqslant |P|</tex>. Заметим, что по определению [[Префикс-функция|префикс-функции]] при <tex>i > |P|</tex> и <tex>p[i] = |P|</tex> подстроки длины <tex>P</tex>, начинающиеся с позиций <tex>0</tex> и <tex>i - |P| + 1</tex>, совпадают. Соберем все такие позиции <tex>i - |P| + 1</tex> строки <tex>S</tex>, вычтем из каждой позиции <tex>|P| + 1</tex>, это и будет ответ. Другими словами, если в какой-то позиции <tex>i</tex> выполняется условие <tex>p[i]=|P|</tex>, то в этой позиции начинается очередное вхождение образца в цепочку. |
| − | + | ||
| + | |||
[[Файл:kmp_pict2.png|640px]] | [[Файл:kmp_pict2.png|640px]] | ||
==Псевдокод== | ==Псевдокод== | ||
| − | '''int'''[] kmp('''string''' | + | '''int'''[] kmp('''string''' P, '''string''' T): |
'''int''' pl = P.length | '''int''' pl = P.length | ||
'''int''' tl = T.length | '''int''' tl = T.length | ||
| Строка 17: | Строка 18: | ||
'''for''' i = 0 .. tl - 1 | '''for''' i = 0 .. tl - 1 | ||
'''if''' p[pl + i + 1] == pl | '''if''' p[pl + i + 1] == pl | ||
| − | answer[count++] = i | + | answer[count++] = i - pl |
'''return''' answer | '''return''' answer | ||
| Строка 24: | Строка 25: | ||
==Оценка по памяти== | ==Оценка по памяти== | ||
| − | Предложенная реализация имеет оценку по памяти <tex>O(P+T)</tex>. Оценки <tex>O(P)</tex> можно добиться за счет | + | Предложенная реализация имеет оценку по памяти <tex>O(P+T)</tex>. Оценки <tex>O(P)</tex> можно добиться за счет запоминания значений префикс-функции для позиций в <tex>S</tex>, меньших <tex>|P| + 1</tex> (то есть до начала цепочки <tex>T</tex>). Это возможно, так как значение префикс-функции не может превысить длину образца, благодаря разделительному символу <tex>\#</tex>. |
| + | |||
| + | ==Замечание== | ||
| + | Вместо [[Префикс-функция|префикс-функции]] в алгоритме Кнута-Морриса-Пратта можно использовать [[Z-функция|Z-функцию]]. Оценки времени работы и памяти при этом не изменятся. | ||
==См. также== | ==См. также== | ||
| Строка 30: | Строка 34: | ||
*[[Алгоритм Бойера-Мура|Алгоритм Бойера-Мура]] | *[[Алгоритм Бойера-Мура|Алгоритм Бойера-Мура]] | ||
*[[Алгоритм Колусси|Алгоритм Колусси]] | *[[Алгоритм Колусси|Алгоритм Колусси]] | ||
| + | *[[Префикс-функция|Префикс-функция]] | ||
| + | *[[Z-функция|Z-функция]] | ||
| − | ==Источники== | + | ==Источники информации== |
| + | *[[wikipedia:en:Knuth–Morris–Pratt algorithm | Wikipedia {{---}} Knuth–Morris–Pratt algorithm]] | ||
*[[wikipedia:ru:Алгоритм Кнута — Морриса — Пратта | Википедия {{---}} Алгоритм Кнута — Морриса — Пратта]] | *[[wikipedia:ru:Алгоритм Кнута — Морриса — Пратта | Википедия {{---}} Алгоритм Кнута — Морриса — Пратта]] | ||
| − | |||
*Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн — Алгоритмы: построение и анализ / пер. с англ. — изд. 2-е — М.: Издательский дом «Вильямс», 2009. — с.1036. — ISBN 978-5-8459-0857-5. | *Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн — Алгоритмы: построение и анализ / пер. с англ. — изд. 2-е — М.: Издательский дом «Вильямс», 2009. — с.1036. — ISBN 978-5-8459-0857-5. | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Поиск подстроки в строке]] | [[Категория: Поиск подстроки в строке]] | ||
| + | [[Категория:Точный поиск]] | ||
Текущая версия на 19:25, 4 сентября 2022
Алгоритм Кнута — Морриса — Пратта (англ. Knuth–Morris–Pratt algorithm) — алгоритм поиска подстроки в строке.
Содержание
Описание алгоритма
Дана цепочка и образец . Требуется найти все позиции, начиная с которых входит в .
Построим строку , где — любой символ, не входящий в алфавит и . Посчитаем на ней значение префикс-функции . Благодаря разделительному символу , выполняется . Заметим, что по определению префикс-функции при и подстроки длины , начинающиеся с позиций и , совпадают. Соберем все такие позиции строки , вычтем из каждой позиции , это и будет ответ. Другими словами, если в какой-то позиции выполняется условие , то в этой позиции начинается очередное вхождение образца в цепочку.
Псевдокод
int[] kmp(string P, string T): int pl = P.length int tl = T.length int[] answer int[] p = prefixFunction(P + "#" + T) int count = 0 for i = 0 .. tl - 1 if p[pl + i + 1] == pl answer[count++] = i - pl return answer
Время работы
Префикс-функция от строки строится за . Проход цикла по строке содержит итераций. Итого, время работы алгоритма оценивается как .
Оценка по памяти
Предложенная реализация имеет оценку по памяти . Оценки можно добиться за счет запоминания значений префикс-функции для позиций в , меньших (то есть до начала цепочки ). Это возможно, так как значение префикс-функции не может превысить длину образца, благодаря разделительному символу .
Замечание
Вместо префикс-функции в алгоритме Кнута-Морриса-Пратта можно использовать Z-функцию. Оценки времени работы и памяти при этом не изменятся.
См. также
Источники информации
- Wikipedia — Knuth–Morris–Pratt algorithm
- Википедия — Алгоритм Кнута — Морриса — Пратта
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн — Алгоритмы: построение и анализ / пер. с англ. — изд. 2-е — М.: Издательский дом «Вильямс», 2009. — с.1036. — ISBN 978-5-8459-0857-5.