Предиктивный синтаксический анализ — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 30 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Для [[LL(k)-грамматики, множества FIRST и FOLLOW | LL(1)-грамматик]] возможна автоматическая генерация парсеров, если известны множества <tex>\mathrm{FIRST}</tex> и <tex>\mathrm{FOLLOW}</tex>. Существуют общедоступные генераторы: ANTLR<ref>[http://www.antlr.org/ ANTLR {{---}} Parser generator]</ref>, Bison<ref>[http://www.gnu.org/software/bison/ Bison {{---}} GNU Project]</ref>, Yacc<ref>[http://dinosaur.compilertools.net/ Lex & Yacc {{---}} A Lexical Analyzer Generator and Yet Another Compiler-Compiler]</ref>, Happy<ref>[https://www.haskell.org/happy/ Happy {{---}} The Parser Generator for Haskell]</ref>. | |
| − | Для [[LL(k)-грамматики, множества FIRST и FOLLOW | LL(1)-грамматик]] возможна автоматическая генерация парсеров, если известны множества FIRST и FOLLOW. Существуют общедоступные генераторы: ANTLR<ref>[http://www.antlr.org/ ANTLR {{---}} Parser generator]</ref>, Bison<ref>[http://www.gnu.org/software/bison/ Bison {{---}} GNU Project]</ref>, Yacc<ref>[http://dinosaur.compilertools.net/ Lex & Yacc {{---}} A Lexical Analyzer Generator and Yet Another Compiler-Compiler]</ref>, Happy<ref>[https://www.haskell.org/happy/ Happy {{---}} The Parser Generator for Haskell]</ref>. | ||
== Общая схема построения рекурсивных парсеров с помощью FIRST и FOLLOW == | == Общая схема построения рекурсивных парсеров с помощью FIRST и FOLLOW == | ||
| − | Пусть <tex>\Gamma</tex> {{---}} LL(1)-грамматика. Построим для нее парсер. | + | Пусть <tex>\Gamma =\langle \Sigma, N, S, P \rangle</tex> {{---}} LL(1)-грамматика. Построим для нее парсер. |
| − | Для каждого нетерминала <tex>A | + | Для каждого нетерминала <tex>A : A \rightarrow \alpha_1 \mid \alpha_2 \mid \ldots \mid \alpha_k </tex> создадим функцию <tex> \mathtt{A}() : \mathtt{Node} </tex>, возвращающую фрагмент [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора#Дерево разбора | дерева разбора]], выведенный из нетерминала <tex>A</tex>. |
| − | Здесь Node {{---}} структура вида: | + | Здесь <tex>\mathtt{Node}</tex> {{---}} структура следующего вида: |
| − | Node | + | '''struct''' Node |
| − | children : list<Node> | + | children : '''list<Node>''' |
| − | value : string // имя нетерминала или текст терминала | + | value : '''string''' <font color="green">// имя нетерминала или текст терминала</font> |
| − | addChild(Node) // функция, подвешивающая поддерево к данному узлу | + | '''function''' addChild('''Node''') <font color="green">// функция, подвешивающая поддерево к данному узлу</font> |
| + | Каждый момент времени парсер работает с определённым '''токеном''' (англ. ''token'') входного слова <tex>s</tex>. Токен {{---}} один или несколько терминалов, объединяемые по смыслу. Примерами токенов могут выступать следующие лексические единицы: | ||
| + | * произвольный символ <tex> c </tex>, | ||
| + | * целое слово, например <tex> public </tex>, | ||
| + | * число со знаком, обозначаемое далее для краткости как <tex> n </tex>. | ||
| + | В общем случае, токеном может являться любое слово, удовлетворяющее произвольному [[Регулярные языки: два определения и их эквивалентность | регулярному выражению]]. | ||
[[Файл:string_token.png|300px]] | [[Файл:string_token.png|300px]] | ||
| − | + | Здесь <tex>\$</tex> обозначает маркер конца строки. | |
| − | curToken {{---}} текущий токен строки. | + | В псевдокоде используются следующие обозначения: |
| + | * <tex>\mathtt{curToken}</tex> {{---}} текущий токен строки, | ||
| + | * <tex>\mathtt{nextToken()}</tex> {{---}} функция, записывающая в <tex>\mathtt{curToken}</tex> следующий за ним токен. | ||
| − | + | Тогда шаблон функции рекурсивного парсера для нетерминала <tex>A</tex> имеет вид: | |
| − | + | A() : '''Node''' | |
| − | A() : Node | + | Node res = Node("A") |
| − | res = Node("A") | + | '''switch''' (curToken) : <font color="green">// принимаем решение в зависимости от текущего токена строки</font> |
| − | switch (curToken) : | + | '''case''' <tex>\mathrm{FIRST}(\alpha_1) \setminus \varepsilon</tex> : |
| − | + | <font color="green">// <tex>\alpha_1 = X_1X_2 \ldots X_{t}</tex> </font> | |
| − | // <tex>\alpha_1 = | + | '''for''' i = 1 .. t |
| − | for | + | '''if''' <tex> X_i </tex> {{---}} терминал |
| − | if <tex> | + | consume(<tex>X_i</tex>) |
| − | consume(<tex> | + | res.addChild(Node(<tex>X_i</tex>)) |
| − | res.addChild( | + | '''else''' <font color="green">// <tex>X_i</tex> {{---}} нетерминал, нужно вызвать соответствующую ему функцию рекурсивного парсера </font> |
| − | + | Node t = <tex>X_i()</tex> | |
| − | else | ||
| − | Node t = <tex> | ||
res.addChild(t) | res.addChild(t) | ||
| − | break | + | '''break''' |
| − | case <tex>FIRST(\alpha_2) \ | + | '''case''' <tex>\mathrm{FIRST}(\alpha_2) \setminus \varepsilon</tex> : |
| − | . | + | <tex>\ldots</tex> |
| − | break | + | '''break''' |
| − | + | <tex>\ldots</tex> | |
| − | + | '''case''' <tex>\mathrm{FIRST}(\alpha_k) \setminus \varepsilon</tex> : | |
| − | error("unexpected char") | + | <tex>\ldots</tex> |
| − | return res | + | '''break''' |
| + | '''case''' <tex>\mathrm{FOLLOW}(A)\ \mathrm{if}\ \exists i : \varepsilon \in \mathrm{FIRST}(\alpha_i)</tex> | ||
| + | res.addChild(Node(<tex>\varepsilon</tex>)) <font color="green">// в этом случае нетерминал раскрывается в <tex>\varepsilon</tex>; можно не добавлять детей к <tex>\mathtt{res}</tex>,</font> | ||
| + | '''break''' <font color="green">// подразумевая, что если у нетерминала <tex>0</tex> детей, то было использовано <tex>\varepsilon</tex>-правило</font> | ||
| + | '''default''' : | ||
| + | <font color="red">error</font>("unexpected char") | ||
| + | '''return''' res | ||
| − | consume(char | + | '''function''' consume(c: '''char''') |
| − | if | + | '''if''' curToken != c |
| − | error(" | + | <font color="red">error</font>("Expected $c but found $curToken") |
nextToken() | nextToken() | ||
| Строка 54: | Строка 64: | ||
== Пример == | == Пример == | ||
| − | Рассмотрим построение парсера на примере LL(1)-грамматики арифметических выражений | + | Рассмотрим построение парсера на примере LL(1)-грамматики арифметических выражений, которая уже была разобрана [[Построение FIRST и FOLLOW#Пример | ранее]]: |
<tex> | <tex> | ||
| Строка 60: | Строка 70: | ||
E' \to +TE' \mid \varepsilon \\ | E' \to +TE' \mid \varepsilon \\ | ||
T \to FT' \\ | T \to FT' \\ | ||
| − | T' \to | + | T' \to * FT' \mid \varepsilon \\ |
F \to n \mid (E) | F \to n \mid (E) | ||
</tex> | </tex> | ||
| − | + | Напомним, что множества <tex>\mathrm{FIRST}</tex> и <tex>\mathrm{FOLLOW}</tex> для неё выглядят так: | |
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
| Строка 84: | Строка 94: | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| <tex>T'</tex> | |style="background-color:#FFF;padding:2px 30px"| <tex>T'</tex> | ||
| − | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ | + | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ *,\ \varepsilon\ \} </tex> |
|style="background-color:#FFF;padding:2px 30px"| <tex>\{\ +,\ \$\ ,\ )\ \}</tex> | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ +,\ \$\ ,\ )\ \}</tex> | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| <tex>F</tex> | |style="background-color:#FFF;padding:2px 30px"| <tex>F</tex> | ||
|style="background-color:#FFF;padding:2px 30px"| <tex>\{\ n,\ (\ \} </tex> | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ n,\ (\ \} </tex> | ||
| − | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ | + | |style="background-color:#FFF;padding:2px 30px"| <tex>\{\ *, \ +,\ \$\ ,\ )\ \} </tex> |
|} | |} | ||
=== Псевдокоды === | === Псевдокоды === | ||
| − | Построим функции обработки некоторых нетерминалов | + | Построим функции обработки некоторых нетерминалов, используя описанный выше шаблон: |
| − | E() | + | E() : '''Node''' |
| − | res = Node("E") | + | Node res = Node("E") |
| − | switch(curToken) | + | '''switch''' (curToken) |
| − | case 'n | + | '''case''' n, '(' : |
res.addChild(T()) | res.addChild(T()) | ||
res.addChild(E'()) | res.addChild(E'()) | ||
| − | break | + | '''break''' |
| − | default : | + | '''default''' : |
| − | error("unexpected char") | + | <font color="red">error</font>("unexpected char") |
| − | return res | + | '''return''' res |
| − | E'() | + | E'() : '''Node''' |
| − | res = Node("E'") | + | Node res = Node("E'") |
| − | switch(curToken) | + | '''switch''' (curToken) |
| − | case '+' : | + | '''case''' '+' : |
consume('+') | consume('+') | ||
res.addChild(Node("+")) | res.addChild(Node("+")) | ||
res.addChild(T()) | res.addChild(T()) | ||
res.addChild(E'()) | res.addChild(E'()) | ||
| − | break | + | '''break''' |
| − | case '$', ')' : | + | '''case''' '$', ')' : |
| − | break | + | '''break''' |
| − | default : | + | '''default''' : |
| − | error("unexpected char") | + | <font color="red">error</font>("unexpected char") |
| − | return res | + | '''return''' res |
| − | F() | + | F() : '''Node''' |
| − | res = Node("F") | + | Node res = Node("F") |
| − | switch(curToken) | + | '''switch''' (curToken) |
| − | case 'n | + | '''case''' n : |
| − | consume( | + | consume(n) |
| − | res.addChild(Node("n | + | res.addChild(Node(curToken)) <font color="green">// <tex>\mathtt{curToken}</tex> подпадает под шаблон <tex>n</tex>, поэтому запишем его в <tex>\mathtt{value}</tex> вершины</font> |
| − | break | + | '''break''' |
| − | case '(' : | + | '''case''' '(' : |
consume('(') | consume('(') | ||
res.addChild(Node("(")) | res.addChild(Node("(")) | ||
| Строка 134: | Строка 144: | ||
consume(')') | consume(')') | ||
res.addChild(Node(")")) | res.addChild(Node(")")) | ||
| − | default : | + | '''default''' : |
| − | error("unexpected char") | + | <font color="red">error</font>("unexpected char") |
| − | return res | + | '''return''' res |
Функции для <tex>T</tex> и <tex>T'</tex> строятся аналогично. | Функции для <tex>T</tex> и <tex>T'</tex> строятся аналогично. | ||
| Строка 142: | Строка 152: | ||
=== Дерево разбора === | === Дерево разбора === | ||
| − | Рассмотрим дерево разбора для выражения (1 + 2) * 3 и несколько первых шагов алгоритма рекурсивного разбора. Сначала вызывается функция стартового нетерминала грамматики, то есть <tex>E</tex>. Так как первым токеном является | + | Рассмотрим дерево разбора для выражения <tex>(1 + 2) * 3</tex> и несколько первых шагов алгоритма рекурсивного разбора. Сначала вызывается функция стартового нетерминала грамматики, то есть <tex>E</tex>. Так как первым токеном является <tex>(</tex>, то будет использовано первое правило разбора <tex>TE'</tex>. Поэтому к вершине с меткой <tex>E</tex> добавятся два ребёнка: <tex>T</tex> и <tex>E'</tex>, а рекурсивный разборщик перейдёт к нетерминалу <tex>T</tex>. <tex>\mathrm{curToken}</tex> по-прежнему равен <tex>(</tex>, поэтому в <tex>F</tex> сработает второй <tex>\mathrm{case}</tex>, первым ребёнком добавится <tex>(</tex>, <tex>\mathrm{curToken}</tex> станет равен <tex>1</tex>, а разборщик перейдёт к нетерминалу <tex>E</tex>. После того как выражение после <tex>(</tex>, которое выводится из <tex>E</tex>, будет полностью разобрано, функция рекурсивного разбора для <tex>F</tex> добавит <tex>)</tex> последним сыном к этому нетерминалу. |
Продолжая в том же духе, мы построим всё дерево разбора данного выражения. | Продолжая в том же духе, мы построим всё дерево разбора данного выражения. | ||
| − | [[Файл:parse_ex1.png|400px|thumb|center|Дерево разбора выражения (1 + 2) * 3]] | + | [[Файл:parse_ex1.png|400px|thumb|center|Дерево разбора выражения <tex>(1 + 2) * 3</tex>]] |
== Нерекурсивный нисходящий парсер == | == Нерекурсивный нисходящий парсер == | ||
| − | [[Файл:Parse_table.png| | + | [[Файл:Parse_table.png|400px|right]] |
| + | |||
| + | Рекурсивные разборщики можно генерировать автоматически, зная множества <tex>\mathrm{FIRST}</tex> и <tex>\mathrm{FOLLOW}</tex>, так как они имеют достаточно прозрачный шаблон построения. Альтернативным способом осуществления нисходящего синтаксического анализа является построение нерекурсивного нисходящего парсера. Его можно построить с помощью явного использования [[Стек | стека]] (вместо неявного при рекурсивных вызовах). Такой анализатор имитирует | ||
| + | [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора#Лево- и правосторонний вывод слова | левое порождение]]. | ||
| − | + | Стек нерекурсивного предиктивного синтаксического анализатора содержит последовательность терминалов и нетерминалов и таблицу синтаксического анализа. На стеке располагается последовательность символов грамматики с маркером конца разбора <tex>\perp</tex> на дне. В начале процесса анализа строки стек содержит стартовый нетерминал грамматики непосредственно над символом <tex>\perp</tex>. Таблица синтаксического анализа представляет собой двухмерный массив <tex>\mathcal{M}[A, c]</tex>, где <tex>A</tex> {{---}} нетерминал или <tex>\perp</tex>, <tex> c </tex> {{---}} токен или символ конца строки <tex>\$</tex>. | |
| − | Нерекурсивный | + | Нерекурсивный синтаксический анализатор смотрит на текущий токен <tex> c </tex> входного слова и на символ на вершине стека <tex>A</tex>, а затем принимает решение в зависимости от одного из возникающих ниже случаев: |
| + | * если <tex>A\ =\ \perp\ \land\ c\ =\ \$</tex>, то синтаксический анализатор прекращает работу, так как разбор строки завершён (на картинке это соответствует <tex>\mathrm{ok}</tex>), | ||
| + | * eсли <tex>A = c</tex>, то синтаксический анализатор снимает со стека токен <tex>A</tex> и перемещает указатель текущего токена ленты к следующему токену (то есть вызывает <tex>\mathtt{nextToken}</tex>), таким образом, происходит выброс символа <tex> c </tex> со стека (на картинке данная ситуация соответствует символу <tex>\nearrow</tex>), | ||
| + | * eсли <tex>A</tex> является нетерминалом, то программа рассматривает запись <tex>\mathcal{M}[A,c]</tex> таблицы разбора <tex>\mathcal{M}</tex>. Эта запись представляет собой либо правило грамматики вида <tex>A \to \alpha_i,\ \alpha_i = X_1 X_2 \ldots X_t</tex>, и тогда <tex>\mathcal{M}[A,c]</tex> содержит номер <tex>i</tex> данного правила, либо запись об ошибке, и тогда <tex>\mathcal{M}[A,c] = \varnothing</tex>. Если <tex>\mathcal{M}[A,c] \neq \varnothing</tex>, то синтаксический анализатор замещает на стеке нетерминал <tex> A </tex> правой частью правила с номером <tex> i </tex>, помещая символы правила на стек в обратном порядке, | ||
| + | * во всех остальных случаях парсер выдаёт сообщение об ошибке. | ||
| − | + | Рассмотренные случаи отображены на картинке справа, где блок <tex> N </tex> отвечает нетерминалам грамматики. Из картинки видно, что вместо рассмотрения всех случаев в коде достаточно просто создать таблицу <tex>\mathcal{M}</tex> таким образом, чтобы она учитывала все случаи, что упростит код. | |
| − | |||
| − | |||
| − | |||
=== Псевдокод === | === Псевдокод === | ||
| − | <code> | + | Здесь по-прежнему <tex>\mathtt{curToken}</tex> обозначает текущий токен строки, а <tex>\mathtt{nextToken}</tex> передвигает указатель на следующий токен. |
| − | function nonRecursiveParser( | + | |
| − | + | <code style = "display: inline-block;"> | |
| − | + | '''function''' nonRecursiveParser(): | |
| − | + | st : '''Stack''' | |
| − | + | st.push(<tex>\perp</tex>) | |
| − | + | st.push(<tex>S</tex>) <font color="green">// здесь <tex> S </tex> {{---}} стартовый нетерминал грамматики</font> | |
| − | + | '''while''' s.top() <tex>\neq\ \perp</tex> | |
| − | + | A = st.top() | |
| − | + | '''if''' <tex>\mathcal{M}[A,\ \mathtt{curToken}]\ ==\ \mathrm{ok}</tex> <font color="green">// <tex> A\ ==\ \perp </tex> и <tex>\mathtt{curToken}\ ==\ \$</tex></font> | |
| − | + | '''break''' <font color="green">// разбор строки завершён</font> | |
| − | + | '''else if''' <tex>\mathcal{M}[A,\ \mathtt{curToken}]\ ==\ \nearrow</tex> <font color="green">// выброс</font> | |
| − | else if M[ | + | nextToken() |
| − | + | st.pop() | |
| − | else if M[ | + | вывести в выходной поток терминал, отвечающий <tex>\mathtt{curToken}</tex> |
| − | + | '''else if''' <tex>\mathcal{M}[A,\ \mathtt{curToken}]</tex> {{---}} номер правила <tex>A \to \alpha_i,\ \alpha_i = X_1 X_2 \ldots X_t</tex> | |
| − | for | + | st.pop() |
| − | + | '''for''' k = t '''downto''' 1 | |
| − | + | st.push(<tex>X_k</tex>) | |
| + | вывести в выходной поток нетерминал, отвечающий <tex>A</tex> | ||
| + | '''else''' | ||
| + | <font color="red">error</font>("unexpected symbol") | ||
</code> | </code> | ||
=== Пример === | === Пример === | ||
| − | <tex> | + | Рассмотрим пример работы нерекурсивного парсера на всё той же грамматике арифметических выражений. Для начала пронумеруем все правила: |
| − | + | ||
| − | + | {| style="background-color:#CCC;margin:0.5px" | |
| − | + | !style="background-color:#EEE"| Номер | |
| − | + | !style="background-color:#EEE"| Правило | |
| − | + | |- | |
| − | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>1</tex> | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| <tex>E \to TE'</tex> | |
| − | + | |- | |
| − | </tex> | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>2</tex> |
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>E' \to +TE'</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>3</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>E' \to \varepsilon</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>4</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>T \to FT'</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>5</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>T' \to * FT'</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>6</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>T' \to \varepsilon</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>7</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>F \to n</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>8</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>F \to (E)</tex> | ||
| + | |} | ||
| + | |||
| + | Теперь можно построить часть таблицы <tex>\mathcal{M}</tex>, содержащей отвечающие нетерминалам строки. Её построение легко осуществить, если известны <tex>\mathrm{FIRST}</tex> и <tex>\mathrm{FOLLOW}</tex>. По этим множествам можно понять, какое правило использовать для данного нетерминала при текущем токене. | ||
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
!style="background-color:#EEE"| | !style="background-color:#EEE"| | ||
| − | !style="background-color:#EEE"| n | + | !style="background-color:#EEE;text-align:center;"| <tex>n</tex> |
| − | !style="background-color:#EEE"| ( | + | !style="background-color:#EEE;text-align:center;"| <tex>(</tex> |
| − | !style="background-color:#EEE"| ) | + | !style="background-color:#EEE;text-align:center;"| <tex>)</tex> |
| − | !style="background-color:#EEE"| + | + | !style="background-color:#EEE;text-align:center;"| <tex>+</tex> |
| − | !style="background-color:#EEE"| * | + | !style="background-color:#EEE;text-align:center;"| <tex>*</tex> |
| − | !style="background-color:#EEE"| $ | + | !style="background-color:#EEE;text-align:center;"| <tex>\$</tex> |
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>E</tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>1 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>1 </tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| Строка 214: | Строка 253: | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>E'</tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>3 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>2 </tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>3 </tex> |
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>T</tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>4 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>4 </tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| Строка 230: | Строка 269: | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>T'</tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>6 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>6 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>5 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>6 </tex> |
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>F</tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>7 </tex> |
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>8 </tex> |
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| Строка 246: | Строка 285: | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px | + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>\perp</tex> |
| − | |||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| Строка 253: | Строка 291: | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
|style="background-color:#FFF;padding:2px 30px"| | |style="background-color:#FFF;padding:2px 30px"| | ||
| + | |style="background-color:#FFF;padding:2px;text-align:center;"| <tex>\mathrm{ok}</tex> | ||
|} | |} | ||
| + | |||
| + | На картинке ниже показаны состояния стека на нескольких первых итерациях цикла и указатель на текущий токен. | ||
[[Файл:Parse_stack.png|500px]] | [[Файл:Parse_stack.png|500px]] | ||
Текущая версия на 19:27, 4 сентября 2022
Для LL(1)-грамматик возможна автоматическая генерация парсеров, если известны множества и . Существуют общедоступные генераторы: ANTLR[1], Bison[2], Yacc[3], Happy[4].
Общая схема построения рекурсивных парсеров с помощью FIRST и FOLLOW
Пусть — LL(1)-грамматика. Построим для нее парсер.
Для каждого нетерминала создадим функцию , возвращающую фрагмент дерева разбора, выведенный из нетерминала .
Здесь — структура следующего вида:
struct Node
children : list<Node>
value : string // имя нетерминала или текст терминала
function addChild(Node) // функция, подвешивающая поддерево к данному узлу
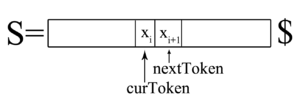
Каждый момент времени парсер работает с определённым токеном (англ. token) входного слова . Токен — один или несколько терминалов, объединяемые по смыслу. Примерами токенов могут выступать следующие лексические единицы:
- произвольный символ ,
- целое слово, например ,
- число со знаком, обозначаемое далее для краткости как .
В общем случае, токеном может являться любое слово, удовлетворяющее произвольному регулярному выражению.
Здесь обозначает маркер конца строки.
В псевдокоде используются следующие обозначения:
- — текущий токен строки,
- — функция, записывающая в следующий за ним токен.
Тогда шаблон функции рекурсивного парсера для нетерминала имеет вид:
A() : Node
Node res = Node("A")
switch (curToken) : // принимаем решение в зависимости от текущего токена строки
case :
//
for i = 1 .. t
if — терминал
consume()
res.addChild(Node())
else // — нетерминал, нужно вызвать соответствующую ему функцию рекурсивного парсера
Node t =
res.addChild(t)
break
case :
break
case :
break
case
res.addChild(Node()) // в этом случае нетерминал раскрывается в ; можно не добавлять детей к ,
break // подразумевая, что если у нетерминала детей, то было использовано -правило
default :
error("unexpected char")
return res
function consume(c: char)
if curToken != c
error("Expected $c but found $curToken")
nextToken()
Такой парсер не только разбирает строку, но и находит ошибки в неудовлетворяющих грамматике выражениях.
Пример
Рассмотрим построение парсера на примере LL(1)-грамматики арифметических выражений, которая уже была разобрана ранее:
Напомним, что множества и для неё выглядят так:
| Правило | FIRST | FOLLOW |
|---|---|---|
Псевдокоды
Построим функции обработки некоторых нетерминалов, используя описанный выше шаблон:
E() : Node
Node res = Node("E")
switch (curToken)
case n, '(' :
res.addChild(T())
res.addChild(E'())
break
default :
error("unexpected char")
return res
E'() : Node
Node res = Node("E'")
switch (curToken)
case '+' :
consume('+')
res.addChild(Node("+"))
res.addChild(T())
res.addChild(E'())
break
case '$', ')' :
break
default :
error("unexpected char")
return res
F() : Node
Node res = Node("F")
switch (curToken)
case n :
consume(n)
res.addChild(Node(curToken)) // подпадает под шаблон , поэтому запишем его в вершины
break
case '(' :
consume('(')
res.addChild(Node("("))
res.addChild(E())
consume(')')
res.addChild(Node(")"))
default :
error("unexpected char")
return res
Функции для и строятся аналогично.
Дерево разбора
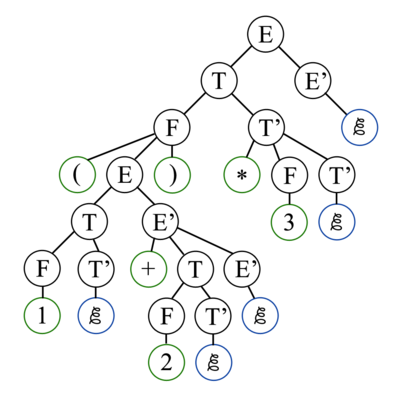
Рассмотрим дерево разбора для выражения и несколько первых шагов алгоритма рекурсивного разбора. Сначала вызывается функция стартового нетерминала грамматики, то есть . Так как первым токеном является , то будет использовано первое правило разбора . Поэтому к вершине с меткой добавятся два ребёнка: и , а рекурсивный разборщик перейдёт к нетерминалу . по-прежнему равен , поэтому в сработает второй , первым ребёнком добавится , станет равен , а разборщик перейдёт к нетерминалу . После того как выражение после , которое выводится из , будет полностью разобрано, функция рекурсивного разбора для добавит последним сыном к этому нетерминалу.
Продолжая в том же духе, мы построим всё дерево разбора данного выражения.
Нерекурсивный нисходящий парсер
Рекурсивные разборщики можно генерировать автоматически, зная множества и , так как они имеют достаточно прозрачный шаблон построения. Альтернативным способом осуществления нисходящего синтаксического анализа является построение нерекурсивного нисходящего парсера. Его можно построить с помощью явного использования стека (вместо неявного при рекурсивных вызовах). Такой анализатор имитирует левое порождение.
Стек нерекурсивного предиктивного синтаксического анализатора содержит последовательность терминалов и нетерминалов и таблицу синтаксического анализа. На стеке располагается последовательность символов грамматики с маркером конца разбора на дне. В начале процесса анализа строки стек содержит стартовый нетерминал грамматики непосредственно над символом . Таблица синтаксического анализа представляет собой двухмерный массив , где — нетерминал или , — токен или символ конца строки .
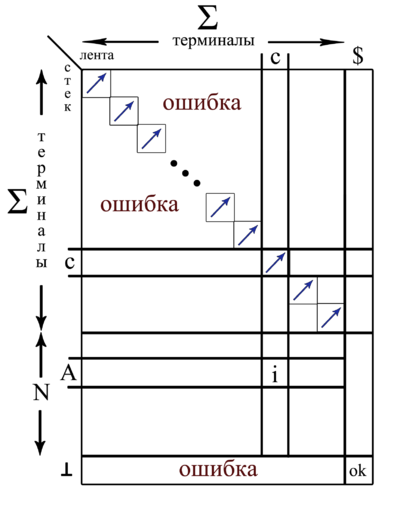
Нерекурсивный синтаксический анализатор смотрит на текущий токен входного слова и на символ на вершине стека , а затем принимает решение в зависимости от одного из возникающих ниже случаев:
- если , то синтаксический анализатор прекращает работу, так как разбор строки завершён (на картинке это соответствует ),
- eсли , то синтаксический анализатор снимает со стека токен и перемещает указатель текущего токена ленты к следующему токену (то есть вызывает ), таким образом, происходит выброс символа со стека (на картинке данная ситуация соответствует символу ),
- eсли является нетерминалом, то программа рассматривает запись таблицы разбора . Эта запись представляет собой либо правило грамматики вида , и тогда содержит номер данного правила, либо запись об ошибке, и тогда . Если , то синтаксический анализатор замещает на стеке нетерминал правой частью правила с номером , помещая символы правила на стек в обратном порядке,
- во всех остальных случаях парсер выдаёт сообщение об ошибке.
Рассмотренные случаи отображены на картинке справа, где блок отвечает нетерминалам грамматики. Из картинки видно, что вместо рассмотрения всех случаев в коде достаточно просто создать таблицу таким образом, чтобы она учитывала все случаи, что упростит код.
Псевдокод
Здесь по-прежнему обозначает текущий токен строки, а передвигает указатель на следующий токен.
function nonRecursiveParser():
st : Stack
st.push()
st.push() // здесь — стартовый нетерминал грамматики
while s.top()
A = st.top()
if // и
break // разбор строки завершён
else if // выброс
nextToken()
st.pop()
вывести в выходной поток терминал, отвечающий
else if — номер правила
st.pop()
for k = t downto 1
st.push()
вывести в выходной поток нетерминал, отвечающий
else
error("unexpected symbol")
Пример
Рассмотрим пример работы нерекурсивного парсера на всё той же грамматике арифметических выражений. Для начала пронумеруем все правила:
| Номер | Правило |
|---|---|
Теперь можно построить часть таблицы , содержащей отвечающие нетерминалам строки. Её построение легко осуществить, если известны и . По этим множествам можно понять, какое правило использовать для данного нетерминала при текущем токене.
На картинке ниже показаны состояния стека на нескольких первых итерациях цикла и указатель на текущий токен.
Примечания
Источники информации
- Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Второе издание. 2008. Стр. 288 — 294.