Фильтр Блума

Определение:

Вероятностное множество (англ. probabilistic set) — структура данных, способная добавлять элемент в множество, а также выполнять запросы проверки принадлежности элемента множеству. При этом существует возможность получить или положительный, но неопределенный ответ (элемента в множестве нет, но структура данных сообщает, что он есть), или отрицательный определенный ответ (элемент точно не содержится в данном множестве).

Неформально вероятностное множество — это структура, позволяющая проверить принадлежность элемента множеству. Ответ может быть:

• элемент точно не принадлежит множеству,
• элемент возможно принадлежит множеству.

Фильтр Блума (англ. Bloom filter) — это реализация вероятностного множества, придуманная Бёртоном Блумом в 1970 году, позволяющая компактно хранить элементы и проверять принадлежность заданного элемента к множеству. При этом существует возможность получить ложноположительное срабатывание (элемента в множестве нет, но структура данных сообщает, что он есть), но не ложноотрицательное.

Фильтр Блума может использовать любой объём памяти, заранее заданный пользователем, причем чем он больше, тем меньше вероятность ложного срабатывания. Поддерживается операция добавления новых элементов в множество, но не удаления существующих (если только не используется модификация со счётчиками). С увеличением размера хранимого множества повышается вероятность ложного срабатывания.

Описание структуры данных

Фильтр Блума с [math]m = 9[/math] и [math]k = 3[/math], хранящий множество из элементов [math]A[/math] и [math]B[/math]. Этот фильтр Блума может определить, что элемент [math]C[/math] входит в множество, хотя он и не добавлен в него.

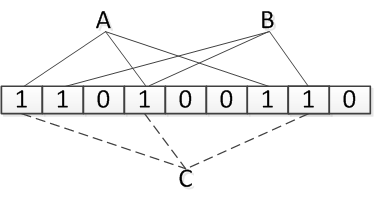
Фильтр Блума представляет собой битовый массив из [math]m[/math] бит и [math]k[/math] различных хеш-функций [math]h_1 \dots h_k[/math], равновероятно отображающих элементы исходного множества во множество [math] \big\{ 0, 1, \dots m - 1 \big\}[/math], соответствующее номерам битов в массиве. Изначально, когда структура данных хранит пустое множество, все [math]m[/math] бит обнулены.

Для добавления элемента [math] e [/math] необходимо записать единицы на каждую из позиций [math]h_1(e) \dots h_k(e)[/math] битового массива.

Чтобы проверить, что элемент [math]e[/math] принадлежит множеству хранимых элементов, необходимо проверить состояние битов [math] h_1(e) \dots h_k(e) [/math]. Если хотя бы один из них равен нулю, элемент не принадлежит множеству. Если все они равны единице, то структура данных сообщает, что элемент принадлежит множеству. При этом может возникнуть две ситуации: либо элемент действительно принадлежит к множеству, либо все эти биты оказались установлены при добавлении других элементов, что и является источником ложных срабатываний в этой структуре данных.

По сравнению с хеш-таблицами, фильтр Блума может обходиться на несколько порядков меньшими объёмами памяти, жертвуя детерминизмом. Обычно он используется для уменьшения числа запросов к несуществующим данным в структуре данных с более дорогостоящим доступом (например, расположенной на жестком диске или в сетевой базе данных), то есть для «фильтрации» запросов к ней.

Минимизация вероятности ложноположительного срабатывания

Пусть размер битового массива [math] m [/math], и заданы [math] k [/math] хеш-функций, причем все хеш-функции выбираются случайным образом. Тогда вероятность, что в [math] j [/math]-ый бит не будет записана единица [math] i [/math]-ой хеш-функцией при вставке очередного элемента, равна:

[math]p(h_i(x) \neq j) = 1 - \dfrac {1}{m} [/math]

Так как для упрощения анализа мы предполагаем, что значения хеш-функций являются независимыми в совокупности случайными величинами, то вероятность, что [math] j [/math]-ый бит останется нулевым после добавления очередного элемента, равна:

[math]p(h_i(x) \neq j[/math] для [math] \forall i \in \big\{ 1 \dots k \big\}) = (1 - \dfrac {1}{m})^k [/math]

А вероятность того, что [math] j [/math]-ый бит будет равен нулю после вставки [math] n [/math] различных элементов в изначально пустой фильтр:

[math](1 - \dfrac {1}{m})^{kn} [/math]

В силу второго замечательного предела и достаточно большого [math] m [/math] можем это записать как:

[math](1 - \dfrac {1}{m})^{kn} \approx e^{-kn/m}[/math]

Ложноположительное срабатывание происходит тогда, когда для несуществующего элемента все [math] k [/math] бит окажутся ненулевыми, и фильтр Блума ответит, что он входит в число вставленных элементов. Тогда вероятность такого события равна:

[math](1 - e^{-kn/m})^k[/math]

Для фиксированных [math] m [/math] и [math] n [/math], оптимальное число хеш-функций [math] k [/math], минимизирующих вероятность ложноположительного срабатывания, равно:

[math]k = \ln 2 \dfrac {m}{n} \approx 0.6931 \dfrac {m}{n}[/math]

Свойства

Фильтр Блума может хранить универсальное множество всех возможных элементов. При этом все ячейки битового массива будут содержать [math] 1 [/math].

При существовании двух фильтров Блума одинаковых размеров и с одинаковыми наборами хеш-функций, их объединение и пересечение может быть реализовано с помощью побитовых операций [math] \vee [/math] и [math]\wedge [/math] .

Примеры реализации фильтра Блума

В ответ на запрос поиска есть вероятность получить положительный ответ, даже если этого элемента в данном множестве нет. Но если же ответ фильтра был отрицательным, запрашиваемого элемента точно нет. Чем больше размер этого множества, тем меньше вероятность получить некорректный ответ на запрос о наличии какого-либо элемента.

• Google BigTable использует фильтры Блума, пример вероятностного множества, для уменьшения числа обращений к жесткому диску при проверке на существование заданной строки или столбца в таблице базы данных. Такой подход к нахождению необходимого элемента в базе данных значительно ускоряет сам процесс поиска и уменьшает количество обращений к жесткому диску,
• компьютерные программы для проверки орфографии,
• Bitcoin использует фильтр Блума, чтобы ускорить синхронизацию с кошельком.

Источники информации

• Википедия — Фильтр Блума
• Wikipedia — Bloom filter
• Demetrescu, Camil. «Experimental Algorithms» — «Springer», 2007 г. — 108-121 стр. — ISBN 978-3-540-72844-3