Игра «Жизнь» — различия между версиями
Mariashka (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 15 промежуточных версий 2 участников) | |||
| Строка 11: | Строка 11: | ||
: '''Правило 8.''' Игра прекращается, если конфигурация на очередном шаге в точности повторит себя же на одном из более ранних шагов. | : '''Правило 8.''' Игра прекращается, если конфигурация на очередном шаге в точности повторит себя же на одном из более ранних шагов. | ||
| − | == | + | == Булевы функции == |
{{Теорема | {{Теорема | ||
| − | |statement = | + | |statement = В игре «Жизнь» можно построить любую булеву функцию. |
|proof = | |proof = | ||
| − | [[Файл:Types.png|250px|right]] | + | [[Файл:Types.png|250px|thumb|right|Базовые конструкции]] |
[[Файл:Glidergun.png|200px|thumb|right| Glider gun]] | [[Файл:Glidergun.png|200px|thumb|right| Glider gun]] | ||
[[Файл:Eater.png|150px|thumb|right| Glider eater]] | [[Файл:Eater.png|150px|thumb|right| Glider eater]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Базовые конструкции=== | ===Базовые конструкции=== | ||
| − | Рассмотрим базовые конструкции необходимые для построения | + | Рассмотрим базовые конструкции необходимые для построения. |
| − | + | ||
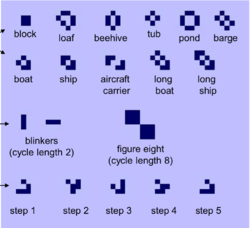
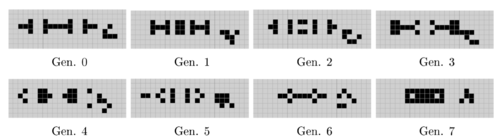
| − | В игры | + | В игры «Жизнь» можно построить различные конструкции (см. рис.): |
| − | * стабильные {{---}} не меняются с течением времени(первые два ряда), | + | * стабильные {{---}} не меняются с течением времени (первые два ряда), |
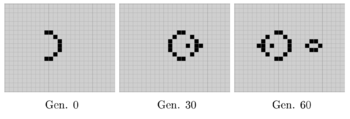
* циклические {{---}} принимают исходное положение каждые <tex>n</tex> итераций (третий ряд), | * циклические {{---}} принимают исходное положение каждые <tex>n</tex> итераций (третий ряд), | ||
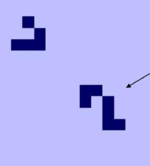
| − | * планер (glider) {{---}} фигура, которая смещается на одну клетку вниз и в право каждые <tex>4</tex> итерации ( | + | * планер (glider) {{---}} фигура, которая смещается на одну клетку вниз и в право каждые <tex>4</tex> итерации (четвертый ряд), |
* космический корабль {{---}} фигура, которая смещается ортогонально на <tex>1</tex> клетку каждые <tex>4</tex> итерации, | * космический корабль {{---}} фигура, которая смещается ортогонально на <tex>1</tex> клетку каждые <tex>4</tex> итерации, | ||
* glider gun {{---}} фигура, бесконечно производящая планер каждые <tex>30</tex> итераций, | * glider gun {{---}} фигура, бесконечно производящая планер каждые <tex>30</tex> итераций, | ||
* glider eater {{---}} фигура, поглощающая планеры. | * glider eater {{---}} фигура, поглощающая планеры. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Булевы функции=== | ===Булевы функции=== | ||
| − | + | Так как <tex>\triangledown</tex> ([[Определение_булевой_функции#.D0.91.D0.B8.D0.BD.D0.B0.D1.80.D0.BD.D1.8B.D0.B5_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B8|штрих Шеффера]] или NAND) является [[Полные системы функций. Теорема Поста о полной системе функций |полной системой]], то достаточно построить <tex>NOT</tex> и <tex>AND</tex>, чтобы показать возможность построения любой булевой функции. | |
| − | < | + | ===Построение NOT=== |
| − | + | Рассмотрим поток данных, состоящий из планеров. Наличие планера {{---}} <tex>1</tex>, отсутствие {{---}} <tex>0</tex>. Добавим поток планеров, состоящий только из <tex>1</tex>. При столкновении планеры исчезают, следовательно на месте <tex>1</tex> образуется <tex>0</tex> и наоборот. | |
| − | < | + | |
| − | |||
| − | |||
| − | |||
| − | |||
[[Файл:Not.png|300px]] | [[Файл:Not.png|300px]] | ||
===Построение AND=== | ===Построение AND=== | ||
| − | См. рисунок. Пусть <tex>AND(x, y)</tex>, тогда y соударяется с <tex>NOT(x)</tex>. Если <tex>NOT(x) = 1</tex>, то на выходе ничего не попадет, если <tex>NOT( x) = 0</tex>, то просто пройдет <tex>y</tex>. | + | См. рисунок. Пусть <tex>AND(x, y)</tex>, тогда y соударяется с <tex>NOT(x)</tex>. Если <tex>NOT(x) = 1</tex>, то на выходе ничего не попадет, если <tex>NOT( x) = 0</tex>, то просто пройдет <tex>y</tex>. |
[[Файл:And.png|300px]] | [[Файл:And.png|300px]] | ||
| + | }} | ||
| + | ==Неразрешимость== | ||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Проблема останова игры «Жизнь» неразрешима. | ||
| + | |proof = | ||
| + | [[Файл:TM.png|300px|thumb|right| МТ в игре «Жизнь»]] | ||
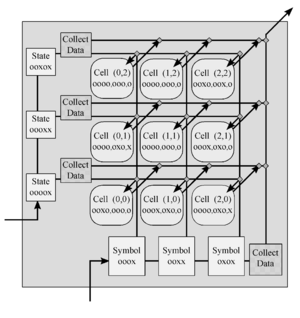
| + | [[Файл:TM_diagram.png|300px|thumb|right| Схема МТ в игре «Жизнь»]] | ||
| + | [[Файл:Finite_state_control.png|300px|thumb|right| Схема конечного автомата в игре «Жизнь»]] | ||
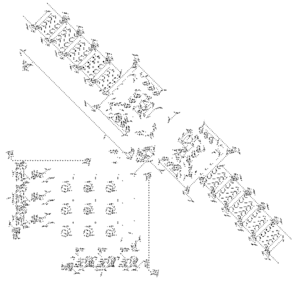
| + | Заметим, что если существует МТ, которая по начальной конфигурации игры «Жизнь» может определить, завершается ли она, то та же МТ может определить останавливается ли любая МТ, что противоречит неразрешимости проблемы останова для МТ. Следовательно, необходимо описать процесс построения МТ в игре «Жизнь». | ||
| + | |||
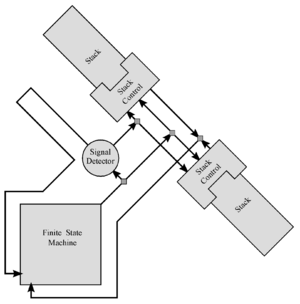
| + | МТ будет состоять из следующих элементов (см.рисунок): | ||
| + | * [[Детерминированные_конечные_автоматы |детерминированный конечный автомат]], | ||
| + | * детектор сигнала, | ||
| + | * [[Стек|стек]], | ||
| + | * контроллер стека. | ||
| + | Мы рассмотрим только общие свойства частей МТ и конструкций, нужных для их построения, так как при построении МТ возникает большое количество технически сложных вспомогательных элементов<ref>[http://eprints.uwe.ac.uk/22323 Rendell, P. (2014) Turing machine universality of the game of life. PhD, University of the West of England]</ref>. | ||
| + | === Конечный автомат === | ||
| + | Конечный автомат представляет собой двумерный массив с двумя входами: предыдущее состояние, получаемое от детектора сигнала, и считанный символ от одного из стеков {{---}} для выбора ряда и колонки ячейки, в которой лежит информация о переходе. | ||
| + | === Детектор сигнала === | ||
| + | Детектор сигнала распознает информацию, полученную от конечного автомата, и передает ее дальше: информацию о следующем состоянии {{---}} обратно в автомат (с задержкой), где она используется для выбора адреса ряда; информацию о символе для записи {{---}} на один из стеков. | ||
| + | === Стек === | ||
| + | Лента МТ представлена в виде двух стеков, которые могут эмулировать передвижение головки чтения записи по ленте: в каждом цикле один стек делает push символа, другой {{---}} pop. | ||
| + | === Контроллер стека === | ||
| + | Контроллер стека производит конструкцию из планеров, необходимую стекам для произведения push или pop, осуществляет перемещение символов. | ||
| + | ===Некоторые конструкции=== | ||
| + | Ниже приведены некоторые конструкций игры, с помощью которых построены вышеупомянутые элементы. | ||
| + | |||
| + | ====Пчелиная королева==== | ||
| + | [[Файл:Queen_bee.png|350px]] | ||
| + | |||
| + | Небольшая конструкция передвигающаяся туда-обратно, при развороте оставляет стабильную конструкцию, называемую ульем. Умирает, если при возвращении улей не исчез. Используется для построения glider gun. | ||
| + | |||
| + | ====Buckaroo==== | ||
| + | Пчелиная королева с eater. Эта конструкция примечательная тем, что при исчезновении улья возникает "вспышка", которая может менять направление планера. | ||
| + | |||
| + | ====Pentadecathlon==== | ||
| + | [[Файл:Pentadecathlon.png|500px]] | ||
| + | |||
| + | Циклическая конструкция, генерирующая небольшую конструкцию, которая может отражать планеры. | ||
}} | }} | ||
== См.также == | == См.также == | ||
| − | * | + | * [[Неразрешимость исчисления предикатов первого порядка]] |
| + | * [[Примеры неразрешимых задач: задача о выводе в полусистеме Туэ|Задача о выводе в полусистеме Туэ]] | ||
| + | * [[Примеры неразрешимых задач: задача о замощении|Задача о замощении]] | ||
| + | * [[Примеры неразрешимых задач: однозначность грамматики|Однозначность грамматики]] | ||
| + | * [[Неразрешимость задачи об эквивалентности КС-грамматик]] | ||
| + | * [[Неразрешимость проблемы существования решения диофантова уравнения в целых числах]] | ||
| + | == Примечания == | ||
| + | <references/> | ||
== Источники информации == | == Источники информации == | ||
* [https://ru.wikipedia.org/wiki/%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_(%D0%B8%D0%B3%D1%80%D0%B0) Википедия {{---}} Жизнь (игра)] | * [https://ru.wikipedia.org/wiki/%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_(%D0%B8%D0%B3%D1%80%D0%B0) Википедия {{---}} Жизнь (игра)] | ||
* [http://academic.regis.edu/dbahr/generalpages/CellularAutomata/CA_part14_files/frame.htm Proving Life is Universal] | * [http://academic.regis.edu/dbahr/generalpages/CellularAutomata/CA_part14_files/frame.htm Proving Life is Universal] | ||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Теория вычислимости]] | ||
| + | [[Категория: Примеры неразрешимых задач]] | ||
Текущая версия на 19:37, 4 сентября 2022
Игра «Жизнь» (англ. Conway's Game of Life) — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970.
Содержание
Правила
- Правило 1. Действие происходит на бесконечной плоскости, разделенной на клетки, которую можно иногда представить как зацикленную конечную.
- Правило 2. Каждая клетка может находиться в двух состояниях: быть живой или быть мёртвой.
- Правило 3. У каждой клетки соседей.
- Правило 4. Если клетка жива и у нее живых соседа, то она остается живой, иначе умирает.
- Правило 5. Если клетка мертва и у нее живых соседа, то она становится живой, иначе остается мертвой.
- Правило 6. Игра прекращается, если на поле не останется ни одной живой клетки.
- Правило 7. Игра прекращается, если при очередном шаге ни одна из клеток не меняет своего состояния.
- Правило 8. Игра прекращается, если конфигурация на очередном шаге в точности повторит себя же на одном из более ранних шагов.
Булевы функции
| Теорема: |
В игре «Жизнь» можно построить любую булеву функцию. |
| Доказательство: |
Базовые конструкцииРассмотрим базовые конструкции необходимые для построения. В игры «Жизнь» можно построить различные конструкции (см. рис.):
Булевы функцииТак как (штрих Шеффера или NAND) является полной системой, то достаточно построить и , чтобы показать возможность построения любой булевой функции. Построение NOTРассмотрим поток данных, состоящий из планеров. Наличие планера — , отсутствие — . Добавим поток планеров, состоящий только из . При столкновении планеры исчезают, следовательно на месте образуется и наоборот. Построение ANDСм. рисунок. Пусть , тогда y соударяется с . Если , то на выходе ничего не попадет, если , то просто пройдет . 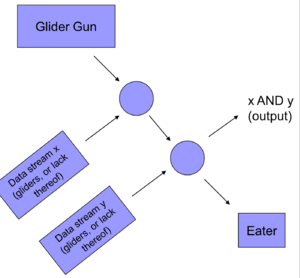 |
Неразрешимость
| Теорема: |
Проблема останова игры «Жизнь» неразрешима. |
| Доказательство: |
|
Заметим, что если существует МТ, которая по начальной конфигурации игры «Жизнь» может определить, завершается ли она, то та же МТ может определить останавливается ли любая МТ, что противоречит неразрешимости проблемы останова для МТ. Следовательно, необходимо описать процесс построения МТ в игре «Жизнь». МТ будет состоять из следующих элементов (см.рисунок):
Мы рассмотрим только общие свойства частей МТ и конструкций, нужных для их построения, так как при построении МТ возникает большое количество технически сложных вспомогательных элементов[1]. Конечный автоматКонечный автомат представляет собой двумерный массив с двумя входами: предыдущее состояние, получаемое от детектора сигнала, и считанный символ от одного из стеков — для выбора ряда и колонки ячейки, в которой лежит информация о переходе. Детектор сигналаДетектор сигнала распознает информацию, полученную от конечного автомата, и передает ее дальше: информацию о следующем состоянии — обратно в автомат (с задержкой), где она используется для выбора адреса ряда; информацию о символе для записи — на один из стеков. СтекЛента МТ представлена в виде двух стеков, которые могут эмулировать передвижение головки чтения записи по ленте: в каждом цикле один стек делает push символа, другой — pop. Контроллер стекаКонтроллер стека производит конструкцию из планеров, необходимую стекам для произведения push или pop, осуществляет перемещение символов. Некоторые конструкцииНиже приведены некоторые конструкций игры, с помощью которых построены вышеупомянутые элементы. Пчелиная королеваНебольшая конструкция передвигающаяся туда-обратно, при развороте оставляет стабильную конструкцию, называемую ульем. Умирает, если при возвращении улей не исчез. Используется для построения glider gun. BuckarooПчелиная королева с eater. Эта конструкция примечательная тем, что при исчезновении улья возникает "вспышка", которая может менять направление планера. PentadecathlonЦиклическая конструкция, генерирующая небольшую конструкцию, которая может отражать планеры. |
См.также
- Неразрешимость исчисления предикатов первого порядка
- Задача о выводе в полусистеме Туэ
- Задача о замощении
- Однозначность грамматики
- Неразрешимость задачи об эквивалентности КС-грамматик
- Неразрешимость проблемы существования решения диофантова уравнения в целых числах