Список с пропусками — различия между версиями
Gaporf (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 82 промежуточные версии 2 участников) | |||
| Строка 3: | Строка 3: | ||
'''Список с пропусками''' (англ. ''skip list'') — вероятностная структура данных, позволяющая в среднем за <tex>O(\log(n))</tex> времени выполнять операции добавления, удаления и поиска элементов. | '''Список с пропусками''' (англ. ''skip list'') — вероятностная структура данных, позволяющая в среднем за <tex>O(\log(n))</tex> времени выполнять операции добавления, удаления и поиска элементов. | ||
| − | + | Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть — на третьем и так далее, но при этом известно, что если элемент расположен на уровне <tex>i</tex>, то он также расположен на всех уровнях, номера которых меньше <tex>i</tex>. | |
==Построение== | ==Построение== | ||
| + | [[Файл:SimpleList.png|thumb|600px|Односвязный отсортированный список]] | ||
| − | Допустим, что нам задан односвязный отсортированный список. | + | [[Файл:SkipList.png|thumb|600px|Получившийся список с пропусками]] |
| + | Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за <tex>O(\log{n})</tex> времени выполнять операции добавления, удаления и поиска элементов. | ||
| + | На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне — всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни. | ||
| − | + | ====Псевдокод==== | |
| + | Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которого есть начало <tex>\mathtt{head} \ </tex> и конец <tex>\mathtt{tail}</tex>. Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне. | ||
| − | + | Элементы односвязного списка — вершины <tex>\mathtt{node}</tex>, у которых есть <tex>3</tex> поля: | |
| + | * <tex>\mathtt{next}</tex> — ссылка на следующий элемент списка на данном уровне | ||
| + | * <tex>\mathtt{key}</tex> — ключ, который хранится в данной вершине | ||
| + | * <tex>\mathtt{down}</tex> — ссылка на соответственный элемент, лежащий уровнем ниже | ||
| + | '''struct''' node: | ||
| + | '''node''' next, down | ||
| + | '''K''' key | ||
| − | + | Также известно, что <tex>\mathtt{head{.}key} = -\infty \ </tex> и <tex>\mathtt{tail{.}key} = \infty</tex>, | |
| + | Функция <tex>\ \mathtt{build\_lvl} \ </tex> возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня. | ||
| − | + | '''list''' build_lvl('''list''' lvl) | |
| + | '''list''' next_lvl | ||
| + | next_lvl.head.down = lvl.head | ||
| + | next_lvl.tail.down = lvl.tail | ||
| + | '''node''' i = lvl.head.next.next | ||
| + | '''node''' cur = next_lvl.head | ||
| + | '''while''' i <tex>\neq</tex> ''null'' '''and''' i.next <tex>\neq</tex> ''null'' | ||
| + | cur.next = node(key, i, cur.next) <font color=darkgreen>// Конструктор node(key, down, next) возвращает новую вершину с ключом key, ссылками down на нижний и next на следующий элемент</font> | ||
| + | cur = cur.next | ||
| + | i = i.next.next <font color=darkgreen>// Переход к следующему чётному элементу</font> | ||
| + | '''return''' next_lvl | ||
| − | + | Функция <tex>\ \mathtt{skip\_list} \ </tex> принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''list''' skip_list('''list''' l): | |
| − | + | '''list''' lvl <font color=darkgreen>// Построение первого уровня</font> | |
| − | '''list''' | + | '''node''' i = l.head |
| − | '''list''' lvl | + | '''node''' j = lvl.head |
| − | ''' | + | '''while''' j <tex>\neq</tex> l.tail |
| − | lvl = | + | i.next = node(j.key, ''null'', j.next) |
| − | '''return''' lvl | + | i = i.next |
| + | j = j.next | ||
| + | '''while''' lvl.size > 2 | ||
| + | lvl = build_lvl(lvl) | ||
| + | '''return''' lvl <font color=darkgreen>// Возвращает ссылку на начало верхнего уровня</font> | ||
==Операции над структурой== | ==Операции над структурой== | ||
===Поиск элемента=== | ===Поиск элемента=== | ||
| − | + | Алгоритм поиска элемента в списке с пропусками состоит из следующих операций: | |
| + | # Начинаем поиск элемента в самом верхнем уровне | ||
| + | # Переходим к следующему элементу списка, пока значение в следующей ячейке меньше | ||
| + | # Переместимся на один уровень вниз и перейти к шагу <tex>2</tex>. Если мы уже на первом уровне — прекратим поиск и вернём ссылку на текущую вершину | ||
| − | В | + | В конце алгоритма функция вернёт элемент, значение которого не меньше ключа <tex>\mathtt{key}</tex> или ссылку на конец списка на первом уровне. |
| − | + | Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет <tex>\log{n}</tex> уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Если же у нас будет <tex>k</tex> уровней, тогда на каждом уровне в среднем будет в <tex>n^{1/k}</tex> раз элементов больше, чем уровнем выше. В таком случае время поиска элемента <tex>-</tex> <tex>O(k \cdot n^{1/k})</tex>. | |
| − | |||
| − | |||
| − | + | ====Псевдокод==== | |
| − | + | Функция <tex>\mathtt{find}</tex> возвращает ссылку на элемент, значение которого не меньше <tex>\mathtt{key}</tex>. В случае, если все элементы в списке с пропусками меньше <tex>\mathtt{key}</tex>, то возвращается ссылка на конец списка с пропусками. | |
| + | |||
| + | '''T''' find('''node''' res, '''K''' key) | ||
| + | '''while''' res.key < key | ||
| + | res = res.next | ||
| + | '''if''' res.down = ''null'' <font color=darkgreen>// Если мы находимся на первом уровне</font> | ||
| + | '''return''' res <font color=darkgreen>// Мы нашли искомый элемент</font> | ||
| + | '''return''' find(res.down, key) <font color=darkgreen>// Иначе спустимся на один уровень ниже</font> | ||
| − | + | Для того, чтобы найти элемент с ключом <tex>\mathtt{key}</tex> в списке с пропусками <tex>\mathtt{skip}</tex> необходимо запустить <tex>\mathtt{find}</tex> следующим образом | |
| − | + | find(skip.head, key) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Вставка элемента=== | ===Вставка элемента=== | ||
| − | + | Алгоритм вставки элементов в список с пропусками состоит из следующих шагов: | |
| − | # | + | # Начинаем вставку на самом верхнем уровне |
| − | # | + | # Переходим к следующему элементу списка пока значение следующей ячейки меньше ключа. |
| − | + | # Если мы на первом уровне — вставляем элемент. Иначе спускаемся ниже и возвращаемся к шагу <tex>2</tex>. Если нам вернули не ''null'' — вставляем элемент на текущем уровне тоже. | |
| − | + | # Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе — ''null''. Если мы были не на первом уровне и нам вернули ''null'' — возвращаем его без броска монетки. | |
| + | |||
| + | Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более чем на один. | ||
| + | |||
| + | Заметим, что вставка элемента <tex>-</tex> поиск элемента и за <tex>O(1)</tex> добавляем не более, чем в <tex>k</tex> уровней элемент. Итого время работы <tex>O(k \cdot n^{1/k})</tex>. | ||
| + | |||
| + | ====Псевдокод==== | ||
| + | Функция <tex>\mathtt{insert} \ </tex> возвращаем ссылку на вставленный элемент в списке, в котором находится <tex>\mathtt{res}</tex>, или ''null'', если на монете выпала «Решка». | ||
| + | |||
| + | '''node''' insert('''node''' res, '''K''' key) | ||
| + | '''while''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key < key | ||
| + | res = res.next | ||
| + | '''node''' down_node | ||
| + | '''if''' res.down = ''null'' | ||
| + | down_node = ''null'' | ||
| + | '''else''' | ||
| + | down_node = insert(res.down, key) | ||
| + | '''if''' down_node <tex>\neq</tex> ''null'' '''or''' res.down = ''null'' <font color=darkgreen>// Если выпал «Орёл» или мы находимся на первом уровне</font> | ||
| + | res.next = node(key, down_node, res.next) | ||
| + | '''if''' coin_flip() = ''head'' <font color=darkgreen>// Если выпал «Орёл»</font> | ||
| + | '''return''' res.next | ||
| + | '''return''' ''null'' | ||
| + | '''return''' ''null'' | ||
| − | + | Для того, чтобы вставить элемент с ключом <tex>\mathtt{key}</tex> в список с пропусками <tex>\mathtt{skip}</tex> необходимо вызвать следующую функцию | |
| − | + | '''function''' insert_element('''list''' skip, '''K''' key) | |
| − | + | '''node''' res = insert(skip.head, key) | |
| − | + | '''if''' res <tex>\neq</tex> ''null'' | |
| − | + | '''list''' lvl | |
| + | lvl.head.next = node(key, res, lvl.tail) | ||
| + | skip = lvl | ||
===Удаление элемента=== | ===Удаление элемента=== | ||
| − | Алгоритм удаления | + | Алгоритм удаления элемента выглядит следующим образом: |
| − | # | + | # Начинаем удалять элемент с верхнего уровня |
| − | # | + | # Переходим к следующему элементу, пока значение следующего элемента меньше ключа |
| + | # Если элемент существует на данном уровне — удаляем его с этого уровня. Если мы не на первом уровне, то удаляем элемент ещё с нижнего уровня. | ||
| + | ====Псевдокод==== | ||
| + | Функция <tex>\mathtt{delete}</tex> удаляет элемент <tex>\mathtt{key}</tex> со всех уровней. | ||
| − | == | + | '''function''' delete('''node''' res, '''K''' key) |
| − | + | '''while''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key < key | |
| + | res = res.next | ||
| + | '''if''' res.down <tex>\neq</tex> ''null'' | ||
| + | delete(res.down, key) | ||
| + | '''if''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key = key | ||
| + | res.next = res.next.next | ||
| − | + | Аналогично со вставкой удаление <tex>-</tex> поиск элемента за <tex>O(k \cdot n^{1/k})</tex> плюс удаление на каждом уровне за <tex>O(1)</tex>. Итого <tex>-</tex> <tex>O(k \cdot n^{1/k})</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Для того, чтобы удалить элемент <tex>\mathtt{key}</tex> из списка с пропусками <tex>\mathtt{skip}</tex>, необходимо вызвать функцию <tex>\mathtt{delete} \ </tex> следующим образом: | |
| − | + | ||
| − | + | delete(skip.head, key) | |
| − | + | ||
| − | + | ==Использование нечестной монеты== | |
| − | + | Вместо честной монеты с распределением <tex>\left\{\dfrac{1}{2}, \ \dfrac{1}{2}\right\}</tex> можно взять в качестве случайного источника нечестную монету с распределением <tex>\{p,q\}</tex> (с вероятностью <tex>p</tex> выпадает «Орёл»). Тогда математическим ожиданием количества элементов на уровне <tex>k</tex> будет <tex>n \cdot p^k</tex>. Время поиска будет равно <tex>O\left( \dfrac{1}{p} \log_{1/p} {n} \right)</tex> <tex>(</tex>на <tex>i</tex>-ом уровне элементов будет почти в <tex>\dfrac{1}{p}</tex> раз больше, чем на <tex>(i+1)</tex>-ом, значит на каждом уровне пройдём не более <tex>\dfrac{1}{p}</tex> элементов, а уровней всего <tex>\log_{1/p} {n}</tex><tex>)</tex>. | |
| − | + | ||
| − | + | Пусть у нас добавлено <tex>n</tex> элементов. Найдём такое распределение <tex>\left\{ p, q \right\}</tex>, при котором функция <tex>\dfrac{1}{x} \log_{1/x} {n}</tex> принимает минимальное значение. Производная этой функции равна <tex>-\dfrac{\ln{n} \left( \ln {(1/x)} - 1 \right)}{x^2 \ln^2{(1/x)}}</tex>. При <tex>x = \dfrac{1}{e}</tex> производная равна нулю, вторая производная в точке <tex>x_0 = \dfrac{1}{e}</tex> больше <tex>0</tex>, значит <tex>x_0</tex> <tex>-</tex> точка минимума. Значит при распределении <tex>\left\{ \dfrac{1}{e}, \dfrac{e - 1}{e} \right\}</tex> время поиска меньше всего. Но не стоит забывать, что это лишь теоретическая оценка и в действительности придумать источник с распределением <tex>\left\{ \dfrac{1}{e}, \dfrac{e - 1}{e} \right\}</tex> почти невозможно, поэтому на практике лучше всего использовать честную монету. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Для крайних распределений: | |
| − | + | * <tex>\{0, 1\}</tex> — <tex>O(n)</tex> — поиск, добавление и удаления элемента, поскольку мы вместо нескольких списков используем по факту один. | |
| − | </ | + | * <tex>\{1, 0\}</tex> — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным <tex>n</tex>, значит время поиска будет равным <tex>O(n)</tex>. |
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Применение== | ==Применение== | ||
| − | * | + | |
| − | * | + | Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ: |
| − | * | + | * Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент) |
| − | + | * Проще реализовать, чем сбалансированные деревья или хеш-таблицы | |
| + | * Следующий элемент достаётся за <tex>O(1)</tex> (при условии, что у нас есть ссылка не текущий) | ||
| + | * Легко модифицировать под различные задачи | ||
| + | |||
| + | ===Нахождение всех отрезков, покрывающих данную точку=== | ||
| + | |||
| + | {{Задача | ||
| + | |definition = Пусть у нас есть запросы двух видов: | ||
| + | # Добавить отрезок <tex>[L, R]</tex> | ||
| + | # Для заданной точки <tex>x</tex> вычислить количество отрезков, которые её покрывают. | ||
| + | Необходимо для каждого запроса второго типа вывести ответ. | ||
| + | }} | ||
| + | |||
| + | Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа <tex>L</tex> и <tex>R</tex> в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем). После этого идём с верхнего уровня, и на каждом уровне мы ищем такие <tex>l</tex> и <tex>r</tex>, что значение <tex>l</tex> меньше <tex>L</tex>, а значение следующего за <tex>l</tex> элемента уже не меньше <tex>L</tex>. Аналогично ищем такое же <tex>r</tex>, только относительно <tex>R</tex>. Если значения <tex>l.next</tex> и <tex>r</tex> лежат полностью внутри отрезка <tex>[L, R]</tex>, то к самому отрезку <tex>[l.next, r]</tex> прибавляем <tex>1</tex>, а сам отрезок <tex>[L, R]</tex> разбиваем на три <tex>[L, l.next.key - 1]</tex>, <tex>[l.next.key, r.key]</tex> и <tex>[r.key + 1, R]</tex> и по отдельности решаем задачу уже для полученных отрезков (если для какого-то отрезка левая граница стала больше правой, то мы ничего не делаем). Допустим, что на каком-то уровне у нас получилось разделить отрезок <tex>[L, R]</tex> на <tex>3</tex> части. Но тогда на следующих уровнях мы будем уменьшать отрезок почти в два раза только с одной стороны, поскольку левая или правая часть отрезка будет равна <tex>l.next.key</tex> или <tex>r.key</tex>. Итого время обработки запроса <tex>O(\log{n})</tex>. | ||
| + | |||
| + | Для запросов второго типа мы снова будем спускать с верхнего уровня до нижнего. На каждом уровне найдём тот элемент, значение которого не меньше точки <tex>x</tex>. Если такой элемент нашёлся, то прибавляем к ответу значение на отрезку между найденным элементом и следующим. Потом также спускаемся на один уровень вниз, если текущий уровень не был первым. Поскольку уровней всего <tex>\log{n}</tex>, а на каждом уровне обойдём не более двух элементов, то данный тип запросов мы обработаем за <tex>O(\log{n})</tex>. | ||
| + | |||
==См. также== | ==См. также== | ||
*[[Список]] | *[[Список]] | ||
*[[Рандомизированное бинарное дерево поиска]] | *[[Рандомизированное бинарное дерево поиска]] | ||
*[[Поисковые структуры данных]] | *[[Поисковые структуры данных]] | ||
| − | + | *[[Skip quadtree: определение, время работы|Skip quadtree]] | |
| − | *[[Skip quadtree: определение, время работы] | ||
| − | |||
==Источники информации== | ==Источники информации== | ||
| − | + | *[http://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D0%B8%D1%81%D0%BE%D0%BA_%D1%81_%D0%BF%D1%80%D0%BE%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%BC%D0%B8 Википедия — списки с пропусками] | |
| − | *[http://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D0%B8%D1%81%D0%BE%D0%BA_%D1%81_%D0%BF%D1%80%D0%BE%D0%BF%D1%83%D1%81%D0%BA%D0%B0%D0%BC%D0%B8 Википедия — списки с пропусками | + | *[http://en.wikipedia.org/wiki/Skip_list Wikipedia — skip list] |
| − | *[http://en.wikipedia.org/wiki/Skip_list | ||
| − | |||
*[http://igoro.com/archive/skip-lists-are-fascinating/ igoro.com — Skip lists are fascinating] | *[http://igoro.com/archive/skip-lists-are-fascinating/ igoro.com — Skip lists are fascinating] | ||
| + | *[http://ticki.github.io/blog/skip-lists-done-right/ ticki.github.io — Skip Lists: Done Right] | ||
| + | *[https://books.google.ru/books?id=NRrcsIJZAYMC&pg=PA157&lpg=PA157&dq=the+interval+skiplist&source=bl&ots=yqad5WH8im&sig=ACfU3U2vzUeMu_psDaWNJ4sztarLzJQsnw&hl=en&sa=X&ved=2ahUKEwi7ta6KyJbhAhWq5aYKHTmPBjgQ6AEwC3oECAkQAQ#v=onepage&q=the%20interval%20skiplist&f=false Eric N. Hanson — A Data Structure for Finding All Intervals That Overlap a Point стр. 155-164] | ||
| + | |||
[[Категория: Структуры данных]] | [[Категория: Структуры данных]] | ||
Текущая версия на 19:15, 4 сентября 2022
Список с пропусками (англ. skip list) — вероятностная структура данных, позволяющая в среднем за времени выполнять операции добавления, удаления и поиска элементов.
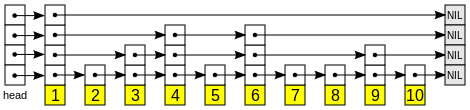
Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть — на третьем и так далее, но при этом известно, что если элемент расположен на уровне , то он также расположен на всех уровнях, номера которых меньше .
Содержание
Построение
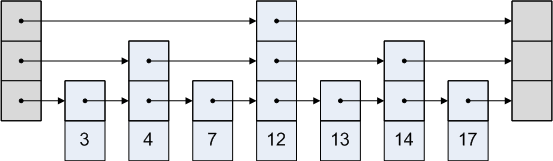
Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за времени выполнять операции добавления, удаления и поиска элементов.
На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне — всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни.
Псевдокод
Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которого есть начало и конец . Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне.
Элементы односвязного списка — вершины , у которых есть поля:
- — ссылка на следующий элемент списка на данном уровне
- — ключ, который хранится в данной вершине
- — ссылка на соответственный элемент, лежащий уровнем ниже
struct node:
node next, down
K key
Также известно, что и ,
Функция возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня.
list build_lvl(list lvl)
list next_lvl
next_lvl.head.down = lvl.head
next_lvl.tail.down = lvl.tail
node i = lvl.head.next.next
node cur = next_lvl.head
while i null and i.next null
cur.next = node(key, i, cur.next) // Конструктор node(key, down, next) возвращает новую вершину с ключом key, ссылками down на нижний и next на следующий элемент
cur = cur.next
i = i.next.next // Переход к следующему чётному элементу
return next_lvl
Функция принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе.
list skip_list(list l):
list lvl // Построение первого уровня
node i = l.head
node j = lvl.head
while j l.tail
i.next = node(j.key, null, j.next)
i = i.next
j = j.next
while lvl.size > 2
lvl = build_lvl(lvl)
return lvl // Возвращает ссылку на начало верхнего уровня
Операции над структурой
Поиск элемента
Алгоритм поиска элемента в списке с пропусками состоит из следующих операций:
- Начинаем поиск элемента в самом верхнем уровне
- Переходим к следующему элементу списка, пока значение в следующей ячейке меньше
- Переместимся на один уровень вниз и перейти к шагу . Если мы уже на первом уровне — прекратим поиск и вернём ссылку на текущую вершину
В конце алгоритма функция вернёт элемент, значение которого не меньше ключа или ссылку на конец списка на первом уровне.
Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Если же у нас будет уровней, тогда на каждом уровне в среднем будет в раз элементов больше, чем уровнем выше. В таком случае время поиска элемента .
Псевдокод
Функция возвращает ссылку на элемент, значение которого не меньше . В случае, если все элементы в списке с пропусками меньше , то возвращается ссылка на конец списка с пропусками.
T find(node res, K key)
while res.key < key
res = res.next
if res.down = null // Если мы находимся на первом уровне
return res // Мы нашли искомый элемент
return find(res.down, key) // Иначе спустимся на один уровень ниже
Для того, чтобы найти элемент с ключом в списке с пропусками необходимо запустить следующим образом
find(skip.head, key)
Вставка элемента
Алгоритм вставки элементов в список с пропусками состоит из следующих шагов:
- Начинаем вставку на самом верхнем уровне
- Переходим к следующему элементу списка пока значение следующей ячейки меньше ключа.
- Если мы на первом уровне — вставляем элемент. Иначе спускаемся ниже и возвращаемся к шагу . Если нам вернули не null — вставляем элемент на текущем уровне тоже.
- Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе — null. Если мы были не на первом уровне и нам вернули null — возвращаем его без броска монетки.
Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более чем на один.
Заметим, что вставка элемента поиск элемента и за добавляем не более, чем в уровней элемент. Итого время работы .
Псевдокод
Функция возвращаем ссылку на вставленный элемент в списке, в котором находится , или null, если на монете выпала «Решка».
node insert(node res, K key)
while res.next null and res.next.key < key
res = res.next
node down_node
if res.down = null
down_node = null
else
down_node = insert(res.down, key)
if down_node null or res.down = null // Если выпал «Орёл» или мы находимся на первом уровне
res.next = node(key, down_node, res.next)
if coin_flip() = head // Если выпал «Орёл»
return res.next
return null
return null
Для того, чтобы вставить элемент с ключом в список с пропусками необходимо вызвать следующую функцию
function insert_element(list skip, K key)
node res = insert(skip.head, key)
if res null
list lvl
lvl.head.next = node(key, res, lvl.tail)
skip = lvl
Удаление элемента
Алгоритм удаления элемента выглядит следующим образом:
- Начинаем удалять элемент с верхнего уровня
- Переходим к следующему элементу, пока значение следующего элемента меньше ключа
- Если элемент существует на данном уровне — удаляем его с этого уровня. Если мы не на первом уровне, то удаляем элемент ещё с нижнего уровня.
Псевдокод
Функция удаляет элемент со всех уровней.
function delete(node res, K key)
while res.next null and res.next.key < key
res = res.next
if res.down null
delete(res.down, key)
if res.next null and res.next.key = key
res.next = res.next.next
Аналогично со вставкой удаление поиск элемента за плюс удаление на каждом уровне за . Итого .
Для того, чтобы удалить элемент из списка с пропусками , необходимо вызвать функцию следующим образом:
delete(skip.head, key)
Использование нечестной монеты
Вместо честной монеты с распределением можно взять в качестве случайного источника нечестную монету с распределением (с вероятностью выпадает «Орёл»). Тогда математическим ожиданием количества элементов на уровне будет . Время поиска будет равно на -ом уровне элементов будет почти в раз больше, чем на -ом, значит на каждом уровне пройдём не более элементов, а уровней всего .
Пусть у нас добавлено элементов. Найдём такое распределение , при котором функция принимает минимальное значение. Производная этой функции равна . При производная равна нулю, вторая производная в точке больше , значит точка минимума. Значит при распределении время поиска меньше всего. Но не стоит забывать, что это лишь теоретическая оценка и в действительности придумать источник с распределением почти невозможно, поэтому на практике лучше всего использовать честную монету.
Для крайних распределений:
- — — поиск, добавление и удаления элемента, поскольку мы вместо нескольких списков используем по факту один.
- — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным , значит время поиска будет равным .
Применение
Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ:
- Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент)
- Проще реализовать, чем сбалансированные деревья или хеш-таблицы
- Следующий элемент достаётся за (при условии, что у нас есть ссылка не текущий)
- Легко модифицировать под различные задачи
Нахождение всех отрезков, покрывающих данную точку
| Задача: |
Пусть у нас есть запросы двух видов:
|
Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа и в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем). После этого идём с верхнего уровня, и на каждом уровне мы ищем такие и , что значение меньше , а значение следующего за элемента уже не меньше . Аналогично ищем такое же , только относительно . Если значения и лежат полностью внутри отрезка , то к самому отрезку прибавляем , а сам отрезок разбиваем на три , и и по отдельности решаем задачу уже для полученных отрезков (если для какого-то отрезка левая граница стала больше правой, то мы ничего не делаем). Допустим, что на каком-то уровне у нас получилось разделить отрезок на части. Но тогда на следующих уровнях мы будем уменьшать отрезок почти в два раза только с одной стороны, поскольку левая или правая часть отрезка будет равна или . Итого время обработки запроса .
Для запросов второго типа мы снова будем спускать с верхнего уровня до нижнего. На каждом уровне найдём тот элемент, значение которого не меньше точки . Если такой элемент нашёлся, то прибавляем к ответу значение на отрезку между найденным элементом и следующим. Потом также спускаемся на один уровень вниз, если текущий уровень не был первым. Поскольку уровней всего , а на каждом уровне обойдём не более двух элементов, то данный тип запросов мы обработаем за .