Самостабилизирующиеся алгоритмы — различия между версиями
Yeputons (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Категория: Параллельное программирование]] | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| Строка 8: | Строка 9: | ||
Тогда от ''любого'' сбоя мы через конечное число шагов будем восстанавливаться без консенсусов и прочих развлечений. | Тогда от ''любого'' сбоя мы через конечное число шагов будем восстанавливаться без консенсусов и прочих развлечений. | ||
== Взаимное исключение == | == Взаимное исключение == | ||
| + | Dijkstra Stabilizing Token Ring Algorithm. | ||
| + | |||
| + | Сначала надо переформулировать задачу: мы говорим, что каждый процесс в системе может либо '''иметь привилегию''', либо не иметь. | ||
| + | В произвольном состоянии системы привилегия может быть у произвольного количества процессов, но через конечное число шагов она остаётся только у одного процесса и мы входим в легальное состояние. | ||
| + | Дальше остаёмся только в легальных состояниях. | ||
| + | |||
| + | TODO: а какие сообщения процессы посылают друг другу? Могут ли быть ошибки (наверное, нет)? Может ли система быть асинхронной (наверное, тоже нет)? | ||
| + | |||
| + | Все $N$ процессов будут замкнуты в кольцо, в котором один процесс назван "первым". | ||
| + | У каждого процесса есть состояние — число от 0 до $K-1$, причём $K \ge N$ — параметр алгоритма. | ||
| + | |||
| + | По определению положим, что у процесса есть привилегия, если: | ||
| + | * Он первый и его значение $S$ совпадает со значением $L$ следующего по часовой стрелке процесса. | ||
| + | * Он не первый и его $S$ не совпадает с $L$. | ||
| + | |||
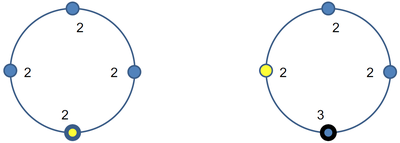
| + | Например, на рисунке ниже толстая граница у выделенного процесса, а жёлтым обозначена привилегия: | ||
| + | |||
| + | [[Файл:distributed-self-stabilization-legal.png|400px]] | ||
| + | |||
| + | Правила перехода в новое состояние: | ||
| + | * Для первого процесса: если была привилегия ($S=L$), то переходим в состояние $(S + 1) \bmod K$ | ||
| + | * Для не-первого процесса: если привилегия есть ($S \neq L$), то переходим в состояние $L$ | ||
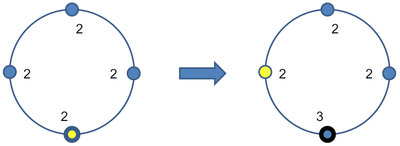
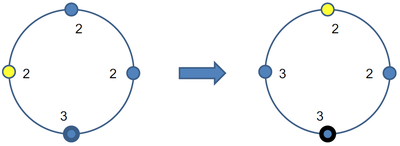
| + | Пример двух переходов: | ||
| + | |||
| + | [[Файл:Distributed-self-stabilization-step-1.png|400px]] | ||
| + | |||
| + | [[Файл:Distributed-self-stabilization-step-2.png|400px]] | ||
| + | |||
| + | Таким образом, в легальном состоянии привилегия у нас ходит по кругу, как в алгоритме с токеном. | ||
| + | Но там потеря токена была смертельной для алгоритма, а у нас — не смертельна. | ||
| + | |||
| + | === Доказательство стабилизируемости === | ||
| + | '''Лемма''': в любом состоянии хотя бы у одного процесса есть привилегия. | ||
| + | В противном случае у нас, с одной стороны, все значения машин равны друг другу (потому что для каждой машины, кроме первой, её значение совпадает со следующей по кругу), а с другой стороны значение первой машины и её соседа должны отличаться, противоречие. | ||
| + | |||
| + | '''Лемма''': что бы не происходило в системе, через $O(N^2)$ шагов в системе первый процесс сделает ход. | ||
| + | '''Доказательство (с лекции)''': если первый процесс не делает ход, то следующий за ним против часовой стрелки процесс 2 сможет сделать максимум один ход: взять себе значение первого процесса. | ||
| + | Процесс 3 после каждого хода процесса 2 может сделать максимум один ход: взять себе значение процесса 2. | ||
| + | То есть процесс 3 может сделать не больше двух ходов (один исходно, один после хода процесса 2). | ||
| + | Аналогично, процесс 4 может сделать не больше трёх ходов, и так далее. | ||
| + | Итого мы получаем, что если первый процесс не делает шаги, то через $O(N^2)$ шагов привилегия полностью исчезнет, чего не бывает. | ||
| + | |||
| + | '''Альтернативное доказательство (проверено рандомом)''': если первый процесс может сделать ход сразу, то всё доказали. | ||
| + | Иначе у него нет привилегии. | ||
| + | Заметим, что если следующий за ним по часовой стрелке процесс 2 либо имеет значение, равное ему, либо отличающееся (тогда он имеет привилегию и сразу делает ход). | ||
| + | Таким образом, через один ход процессы 1 и 2 имеют одинаковые значения. | ||
| + | Аналогично, через два хода процессы 1, 2 и 3 имеют одинаковые значения. | ||
| + | А через $N-1$ шаг все процессы гарантированно имеют одинаковые значения (если первый процесс так и не походил). | ||
| + | Таким образом, через $N-1$ шаг у первого процесса появляется привилегия и он ходит, $N=O(N^2)$. | ||
| + | |||
| + | '''Лемма''': рано или поздно у первого процесса будет уникальное $S$. | ||
| + | '''Доказательство''': все остальные процессы умеют только копировать состояния друг у друга, а первый процесс ходит бесконечно. | ||
| + | Поэтому рано или поздно он перейдёт на состояние, которое не совпадает ни с одним из оставшихся $N-1$ состоянием. | ||
| + | |||
| + | '''Лемма''': через $O(N^2)$ после этого система стабилизируется. | ||
| + | '''Альтернативное доказательство (не с лекции)''': это состояние будет сразу же скопировано на второй процесс, потом сразу же скопировано на третий, и так далее, после чего мы прийдём в состояние, где все значения равны, а оно легальное. | ||
== Поиск остовного дерева == | == Поиск остовного дерева == | ||
| + | Такая задача возникает, например, в internet of things: набросали с вертолёта на поле размером 3км*3км много хрупких устройств со слабыми антеннами, которым надо соединиться в единую сеть. При этом топология связи там неполная и половина устройств подохла. | ||
| + | А мы хотим построить дерево, чтобы узлы могли друг с другом общаться (а не каждый каждому передавать, потому что тогда надо бороться с циклами). | ||
| + | |||
| + | Решение начинается с инициатора (например, узел, которому надо что-нибудь узнать про всех остальных), которому это дерево нужно. | ||
| + | |||
| + | Каждый узел поддерживает у себя $d$ (расстояние до корня) и $p$ (узел-предок в дереве). | ||
| + | Корень всегда ставит у себя $d=0$ и $p=-1$, а остальные узлы в постоянном режиме делают: | ||
| + | * Найти соседа $j$ с минимальным $d_j$ | ||
| + | * Установить его в качестве своего родителя и $d_i=d_j+1$ | ||
| + | |||
| + | Тогда корень стабилизируется сразу, узлы, которым корень виден, стабилизируются через одну итерацию, их соседи — через две, и так далее. | ||
| + | |||
| + | Если какой-нибудь узел выпадает, то его дети найдут себе кого-нибудь ещё и снова встроятся в дерево. | ||
| + | |||
| + | Единственная проблема — если умирает корень, но тогда узнавший об этом узел может инициировать перестроение дерева (если у нас цель — связь). | ||
Текущая версия на 19:24, 4 сентября 2022
| Определение: |
Самостабилизирующие алгоритмы — это идея построения алгоритмов, устойчивых к ошибкам:
|
Тогда от любого сбоя мы через конечное число шагов будем восстанавливаться без консенсусов и прочих развлечений.
Взаимное исключение
Dijkstra Stabilizing Token Ring Algorithm.
Сначала надо переформулировать задачу: мы говорим, что каждый процесс в системе может либо иметь привилегию, либо не иметь. В произвольном состоянии системы привилегия может быть у произвольного количества процессов, но через конечное число шагов она остаётся только у одного процесса и мы входим в легальное состояние. Дальше остаёмся только в легальных состояниях.
TODO: а какие сообщения процессы посылают друг другу? Могут ли быть ошибки (наверное, нет)? Может ли система быть асинхронной (наверное, тоже нет)?
Все $N$ процессов будут замкнуты в кольцо, в котором один процесс назван "первым". У каждого процесса есть состояние — число от 0 до $K-1$, причём $K \ge N$ — параметр алгоритма.
По определению положим, что у процесса есть привилегия, если:
- Он первый и его значение $S$ совпадает со значением $L$ следующего по часовой стрелке процесса.
- Он не первый и его $S$ не совпадает с $L$.
Например, на рисунке ниже толстая граница у выделенного процесса, а жёлтым обозначена привилегия:
Правила перехода в новое состояние:
- Для первого процесса: если была привилегия ($S=L$), то переходим в состояние $(S + 1) \bmod K$
- Для не-первого процесса: если привилегия есть ($S \neq L$), то переходим в состояние $L$
Пример двух переходов:
Таким образом, в легальном состоянии привилегия у нас ходит по кругу, как в алгоритме с токеном. Но там потеря токена была смертельной для алгоритма, а у нас — не смертельна.
Доказательство стабилизируемости
Лемма: в любом состоянии хотя бы у одного процесса есть привилегия. В противном случае у нас, с одной стороны, все значения машин равны друг другу (потому что для каждой машины, кроме первой, её значение совпадает со следующей по кругу), а с другой стороны значение первой машины и её соседа должны отличаться, противоречие.
Лемма: что бы не происходило в системе, через $O(N^2)$ шагов в системе первый процесс сделает ход. Доказательство (с лекции): если первый процесс не делает ход, то следующий за ним против часовой стрелки процесс 2 сможет сделать максимум один ход: взять себе значение первого процесса. Процесс 3 после каждого хода процесса 2 может сделать максимум один ход: взять себе значение процесса 2. То есть процесс 3 может сделать не больше двух ходов (один исходно, один после хода процесса 2). Аналогично, процесс 4 может сделать не больше трёх ходов, и так далее. Итого мы получаем, что если первый процесс не делает шаги, то через $O(N^2)$ шагов привилегия полностью исчезнет, чего не бывает.
Альтернативное доказательство (проверено рандомом): если первый процесс может сделать ход сразу, то всё доказали. Иначе у него нет привилегии. Заметим, что если следующий за ним по часовой стрелке процесс 2 либо имеет значение, равное ему, либо отличающееся (тогда он имеет привилегию и сразу делает ход). Таким образом, через один ход процессы 1 и 2 имеют одинаковые значения. Аналогично, через два хода процессы 1, 2 и 3 имеют одинаковые значения. А через $N-1$ шаг все процессы гарантированно имеют одинаковые значения (если первый процесс так и не походил). Таким образом, через $N-1$ шаг у первого процесса появляется привилегия и он ходит, $N=O(N^2)$.
Лемма: рано или поздно у первого процесса будет уникальное $S$. Доказательство: все остальные процессы умеют только копировать состояния друг у друга, а первый процесс ходит бесконечно. Поэтому рано или поздно он перейдёт на состояние, которое не совпадает ни с одним из оставшихся $N-1$ состоянием.
Лемма: через $O(N^2)$ после этого система стабилизируется. Альтернативное доказательство (не с лекции): это состояние будет сразу же скопировано на второй процесс, потом сразу же скопировано на третий, и так далее, после чего мы прийдём в состояние, где все значения равны, а оно легальное.
Поиск остовного дерева
Такая задача возникает, например, в internet of things: набросали с вертолёта на поле размером 3км*3км много хрупких устройств со слабыми антеннами, которым надо соединиться в единую сеть. При этом топология связи там неполная и половина устройств подохла. А мы хотим построить дерево, чтобы узлы могли друг с другом общаться (а не каждый каждому передавать, потому что тогда надо бороться с циклами).
Решение начинается с инициатора (например, узел, которому надо что-нибудь узнать про всех остальных), которому это дерево нужно.
Каждый узел поддерживает у себя $d$ (расстояние до корня) и $p$ (узел-предок в дереве). Корень всегда ставит у себя $d=0$ и $p=-1$, а остальные узлы в постоянном режиме делают:
- Найти соседа $j$ с минимальным $d_j$
- Установить его в качестве своего родителя и $d_i=d_j+1$
Тогда корень стабилизируется сразу, узлы, которым корень виден, стабилизируются через одну итерацию, их соседи — через две, и так далее.
Если какой-нибудь узел выпадает, то его дети найдут себе кого-нибудь ещё и снова встроятся в дерево.
Единственная проблема — если умирает корень, но тогда узнавший об этом узел может инициировать перестроение дерева (если у нас цель — связь).